Induktion durch Drehen einer Spule
 |
Auch in einer Spule, die sich in einem homogenen Magnetfeld dreht, wird
eine Spannung induziert. |
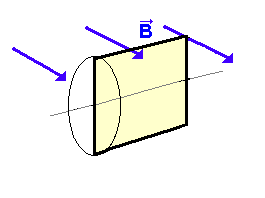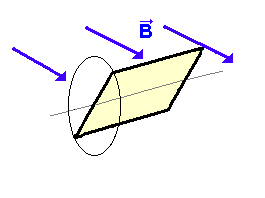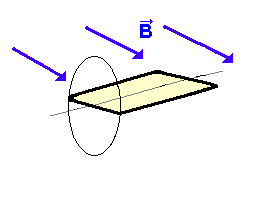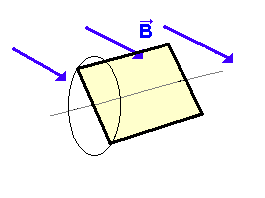
| (1) Betrachtung einer Fläche orthogonal zu den Magnetfeldlinien. Um das Verständnis und die Argumentation zu erleichtern, betrachten wir eine gedachte Fläche As (hellblau gezeichnet). Sie ist senkrecht zu magnetischen Feldlinien orientiert. Diese Fläche geht aus der eigentlichen Spulenfläche (gelb) durch Projektion hervor. |
|
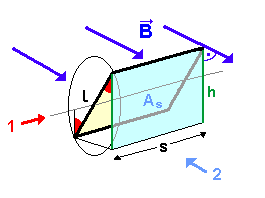 |
Die eigentliche Spulenfläche ist : A=L * s Wie hängen die eigentliche Spulenfläche A und die senkrecht gedachte Fläche As miteinander zusammen? |
| Aus der Richtung 1 betrachet, können wir folgenden Zusammenhang zwischen der Seitenlänge L und der Höhe h in dem rechtwinkligen Dreieck erkennen: |
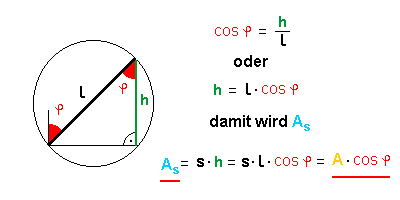 |
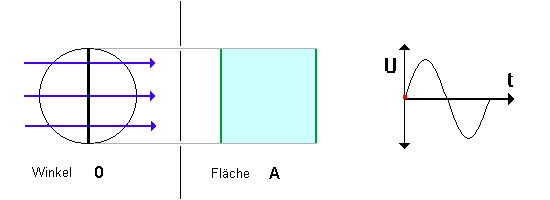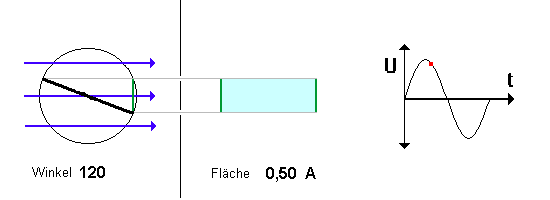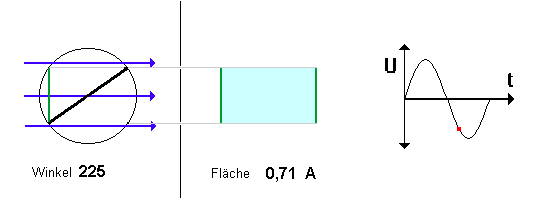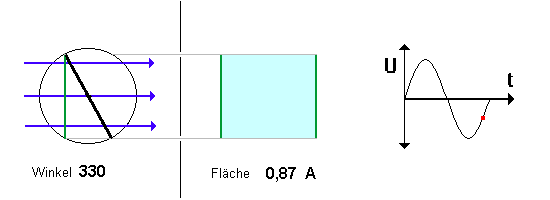
| (2) Die Fläche As ändert sich bei der Drehung ! Da sich die Spule ständig dreht, und sich so der Winkel laufend
ändert, verändert sich damit auch die vom Magnetfeld senkrecht
durchsetzte Fläche As.
|
|
 |
| (3) Wann ist die induzierte Spannung maximal ? |
|
| Eine vorschnelle Antwort lautet: dann, wenn die Fläche As maximal ist. |
|
 |
Doch Vorsicht !! |
| Betrachte die Simulation oben noch
einmal genau, Daher ist die induzierte Spannung dann besonders groß, wenn die Spule
praktisch "waagrecht liegt". Beachte hierzu auch den Verlauf des roten Punktes
im U-t-Diagramm. |
|
| (4) Die Zeit kommt ins Spiel. |
|
| Rotiert die Spule gleichförmig, so ändert sich
der Winkel proportional zu der Zeit t; |
|
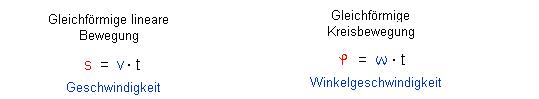
|
|
| Für die Winkelgeschwindigkeit gilt auch, wobei f die Drehfrequenz bzw. T die Umlaufdauer ist : |
|
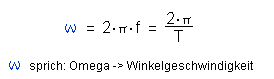
|
|
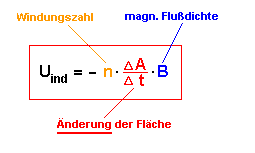
| Für den Momentanwert der auftretenden induzierten Wechselspannung gilt nun: |
|
 |
|
| (5) Konsequenzen aus der Gleichung. |
|
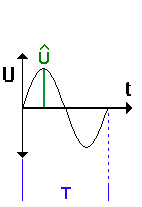
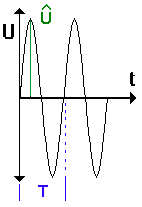
| In den Darstellungen unten erkennt man noch einmal die Bedeutung des Scheitelwertes der Spannung: dies ist der größte in der Wechselspannung auftretende Spannungswert. Weil in dem Ausdruck für den Scheitelwert auch die
Winkelgeschwindigkeit vorkommt - formal eine Folge der inneren Ableitung -
hängt der Scheitelwert der Wechselspannung auch von der Drehfrequenz
ab: |
|
 |
 |
|
|
|
Dies führt dazu, dass sie - ähnlich wie gegeneinandergeschaltete Batterien - einander entgegenwirken können, und so die Gesamtspannung zweier Generatoren im Extremfall auch 0 werden kann. Bevor ein Generator also "ans Netz geht", muß die Drehfrequenz und die Phasenlage mit den anderen Generatoren im Netz synchronisiert werden. |
|
| Grüninger, Landesbildungsserver, 2003 |
|


