Magnetfeld, Flussdichte und der magnetische Fluss.

1.) Das Magnetfeld.

Magnetfelder haben Vektoreigenschaften, sie werden vollständig durch zwei Eigenschaften beschrieben:

• ihre Richtung

	Hier verlaufen die Magnetfeldlinien aus der Zeichenebene heraus auf dich zu, wie ein Pfeil, der dir entgegen fliegt.
	Hier verlaufen die Magnetfeldlinien in die Zeichenebene hinein von dir weg, wie ein Pfeil, dem du hinterher siehst.
	Für uns ist hier die Richtung nicht wichtig. Der blaue Punkt kennzeichnet also eine Magnetfeldlinie die entweder in die Zeichenebene hinein oder aus der Zeichenebene heraus zeigt.

• ihren Betrag

Die Stärke des Feldes kennzeichnen wir dadurch wie dicht die einzelnen Feldlinien beieinander liegen.
Die Stärke des Feldes nennt man auch magnetische Flussdichte B.

	Hier liegen die Feldlinien weit auseinander, die Stärke des Feldes ist also klein. (kleine magnetische Flussdichte)
	Hier liegen die Feldlinien eng beieinander. Dies kennzeichnet eine große Stärke des Magnetfeldes. (große magnetische Flussdichte)
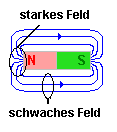	Denke auch an das Feldlinienbild eines Stabmagneten. An den Polen ist das Feld kräftig, hier sind die Feldlinien eng beieinander. Außen am Magnet sind die Feldlinien weit voneinander entfernt, das Feld ist hier schwach.

2.) Der magnetische Fluss.

Ein Magnetfeld durchsetzt die Fläche einer Spule. Der magnetische Fluss ist anschaulich die Zahl aller Feldlinien, die senkrecht durch die Oberfläche einer Spule gehen. Das Symbol für den magnetischen Fluss ist das große griechische "Phi", das man so schreibt: Φ Der Betrag des magnetischen Flusses Φ hängt von zwei Größen ab:

von der Fläche A der Spule		von der magnetischen Flussdichte B (Stärke des Magnetfeldes)
gleiche Flussdichte B, verschiedene Flächen A		gleiche Flächen A, verschiedene Flussdichten B
große Fläche -> großer Fluss	kleine Fläche -> kleiner Fluss	große Flussdichte starkes Feld -> großer Fluss	kleine Flussdichte schwaches Feld -> kleiner Fluss
54 Feldlinien	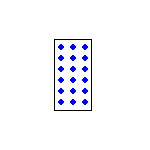18 Feldlinien	großer Fluss" TITLE="große Flussdichte -> großer Fluss"> 54 Feldlinien	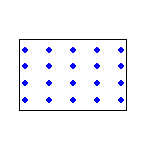20 Feldlinien

Bringe folgende Ideen nicht durcheinander:
magnetischer Fluss Φ: Gesamtzahl aller Feldlinien, die senkrecht durch eine (beliebig große) Fläche gehen.
magnetische Flussdichte B: wie dicht die Feldlinien beieinander liegen, die Zahl der Feldlinien je cm²

3.) Die Induktionsspannung.

Eine Induktionsspannung kann in der Spule nur entstehen, wenn sich der magnetische Fluss in der Spule ändert.
Dabei gibt es zwei Möglichkeiten:

Je größer die Änderungsrate ΔΦ / Δt des magnetischen Fluss ist (d.h. anschaulich, je schneller sich die Gesamtzahl der Feldlinien in der Spule verändert), desto größer ist die induzierte Spannung.
Die vom Magnetfeld durchsetzte Fläche ist hellblau gezeichnet.

Da der magnetische Fluss das Produkt der Flussdichte B und der Fläche A ist, ist die Einheit des Flusses also:
1 T * m² = 1 Weber = 1 Wb.

Fragen / Aufgaben:

A) Induktion durch Flächenänderung

(1)

Klicke zunächst Start. (ohne Änderung der Grundeinstellungen)

• Wie ändert sich die Zahl der Feldlinien in jeder Sekunde?
• Wie groß ist die Änderungsrate des Flusses?

Nach oben zum Applet

(2)

Wähle nun bei Spulenfläche "kleine Fläche" aus und wiederhole das Experiment.

Vergleiche folgende Größen mit denen aus Versuch (1):

• die magnetische Flussdichte B (wie dicht die Feldlinien liegen)
• die Zeit t für das Einbringen ins Feld
• die Gesamtzahl der Feldlinien, welche die Spule durchsetzen.
• die Änderungsrate des magnetischen Flusses.

Nach oben zum Applet

(3)

Wähle diesmal wieder bei Spulenfläche "große Fläche" und bei Stärke des Feldes "schwaches Feld".

Vergleiche wieder folgende Größen mit denen aus Versuch (1) und (2):

• die magnetische Flussdichte B (wie dicht die Feldlinien liegen)
• die Gesamtzahl der Feldlinien, welche die Spule durchsetzen.
• die Änderungsrate des magnetischen Flusses.

Nach oben zum Applet

(4)

Belasse Spulenfläche und Stärke des Feldes wie bei (3) wähle aber nun bei Änderungsrate "1 s / 1.2 s" aus.

Vergleiche auch nun wieder diese Größen mit denen aus Versuch (3):

• die Zeit t für das Einbringen ins Feld
• die Gesamtzahl der Feldlinien, welche die Spule durchsetzen.
• die Änderungsrate des magnetischen Flusses.

Nach oben zum Applet

(5)

Verändere nun die Einstellungen bei Spulenfläche, Stärke des Feldes und Änderungsrate.

• Welche Einstellungen musst du wählen, damit die Änderungsrate des Flusses maximal wird?
• Was geschieht, wenn du bei Flussänderung "abnehmender Fluss" wählst?
• Was bedeutet dies für die Änderungsrate des Flusses?
• Was bedeutet dies für die induzierte Spannung?

Nach oben zum Applet

B) Induktion durch Ändern der magnetischen Flussdichte.

Wähle nun folgende Einstellungen:

Induktionstyp: konstante Fläche - veränderl. Feld
Flussänderung: zunehmender Fluss
Spulenfläche: große Fläche
Stärke des Feldes: starkes Feld
Änderungsrate: 10 s / 12 s

(6)

Klicke einfach "Start"

• Wie verändert sich die Gesamtzahl der Feldlinien nun je Sekunde?
• Woran merkt man, dass sich diesmal die magnetische Flussdichte B verändert?
• Wie groß ist die Änderungsrate des magnetischen Flusses?

Nach oben zum Applet

(7)

Setze die Änderungsrate nun auf 1 s / 1.2 s.

• Wie lange dauert das Anwachsen des Flusses diesmal?
• Wie groß ist also die Änderungsrate nun?
• Was bedeutet dies für die induzierte Spannung?

Nach oben zum Applet

(8)

Belasse die Änderungsrate bei 1 s / 1.2 s und wähle diesmal als Spulenfläche "kleine Fläche" aus.
(N.B. Feldlinien die gerade an der Kante des Spulenrahmens auftauchen gelten als zur Hälfte in der Spulenfläche und zur Hälfte draußen).

• Welchen Einfluss hat dies auf die Änderungsrate des Flusses?
• Wie ändert sich also die induzierte Spannung?

Nach oben zum Applet

(9)

Verändere nun alle Einstellungen außer Induktionstyp.

• Wie bekommt man die Änderungsrate des Flusses und damit die Induktionsspannung möglichst groß?
• Wie wird sie möglichst klein?

Nach oben zum Applet

Ein Arbeitsblatt zu den Aufgaben von oben gibt es hier: Arbeitsblatt Fluss

Ob du alles verstanden hast, kannst du hier kontrollieren: Lösungen zur Seite

Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:

Sie müssen dazu die gepackte Datei (fluss.zip) herunterladen und in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder. Die nötigen Java-Achive sind ebenfalls enthalten.

Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.

Nutzungsbedingungen:

Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und Kollegen weitergeben.

Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der ausdrücklichen Zustimmung.

Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang Christian und Mario Belloni vom Davidson College, USA   (Copyright Hinweise) © Javascript dieses Problems: Klaus-Dieter Grüninger, Landesbildungsserver Baden-Württemberg, 2011