Die Leiterschleife im Magnetfeld - Flächenänderung
Eine andere Betrachtungsweise:
die vom Magnetfeld durchsetzte Fläche ändert sich.
Für die Wiedergabe der Simulationen auf dieser Seite benötigt
man die Java-Runtime-Environment. Das Laden und Aktivieren der Java-Applets benötigt etwas Zeit.
Bitte nicht "Start" klicken, bevor das Applet vollständig
geladen ist. |
1.) Was wir schon gelernt haben....
Bisher haben wir das Auftreten der Induktionsspannung mit Hilfe der
Lorentzkräfte erklärt.
Bewegt man eine Leiterschleife in ein Magnetfeld hinein, so tritt erst dann eine Induktionsspannung an den Anschlüssen auf, wenn das erste Leiterstück (a) das Feld erreicht hat. Die Induktionsspannung ist so lange messbar, bis das zweite Leiterstück (b) in das Magnetfeld eintritt.
Bewegt man die Leiterschleife aus dem Magnetfeld, so tritt erst dann eine Induktionsspannung an den Anschlüssen auf, wenn das obere Leiterstück (b) das Magnetfeld verlässt. Sie ist so lange messbar, bis auch das untere Leiterstück (a) das Magnetfeld verlässt.
2.) Ein neuer Aspekt bringt uns weiter.
Eine Induktionsspannung tritt also immer dann auf, wenn die Spule in das Magnetfeld eindringt oder das Magnetfeld verlässt. Wird die Spule ganz außerhalb des Feldes bewegt, oder bewegt sie sich ganz im Magnetfeld, so tritt keine Induktionsspannung auf.
Man kann das auch so ausdrücken:
Eine Induktionsspannung tritt immer nur dann auf, wenn der
Anteil der Spulenfläche, der vom Magnetfeld
durchsetzt wird, sich verändert.
Dieser Aspekt soll hier näher untersucht werden.
Fragen / Aufgaben:
1.) Bewegung in das Magnetfeld.
Belasse zunächst die Grundeinstellungen und klicke "Start".
- Achte darauf, wie sich die blau ausgefüllte Fläche verändert. (auch Anzeige "Fläche" )
- Wann ist an den Anschlüssen links eine Induktionsspannung messbar? (rot eingetragene Pole, Anzeige Spannung)
- Wie sieht das Fläche(Zeit) Diagramm der Bewegung aus?
- Wie sieht das Induktionsspannung(Zeit) Diagramm aus?
2.) Bewegung aus dem Magnetfeld.
Ändere "Bewegungsrichtung" auf "aus dem Feld / nach oben".
- Achte darauf, wie sich die blau ausgefüllte Fläche verändert. (auch Anzeige "Fläche" )
- Wann ist an den Anschlüssen links eine Induktionsspannung messbar? (rot eingetragene Pole, Anzeige Spannung)
- Vergleiche die Polung der Induktionsspannung bei 1.) und bei 2.).
- Wie sieht das Fläche(Zeit) Diagramm der Bewegung nun aus?
- Wie sieht das Induktionsspannung(Zeit) Diagramm aus?
3.) Die Flächenänderung hängt von der Geschwindigkeit v ab.
Wie die Induktionsspannung von der Stärke des Magnetfeldes (Flussdichte
B) und der Windungszahl abhängt, wissen wir bereits.
Wir verändern hier nichts an den Grundeinstellungen
(v = 0,02 m/s ; B = 0,01 T ; n = 100 ; Bewegung in
das Feld).
- Welche Zeit Δt benötigt die Spule bei einer Geschwindigkeit von 0,02 m/s um in das Feld zu gelangen?
- Welche Höhe h hat also die Spule?
- Wie groß ist die Induktionsspannung Uind bei dieser Einstellung?
Verdopple die Geschwindigkeit auf 0,04 m/s.
- Welche Zeit Δt benötigt die Spule bei doppelter Geschwindigkeit (0,04 m/s) um ins Feld zu gelangen?
- Wie verändert sich dadurch das Fläche(t)-Diagramm? (oberes Diagramm - blaue Kurve)
- Vergleiche die Steigung der blauen Kurve ("Geschwindigkeit der Flächenänderung") bei beiden Geschwindigkeiten (bei 0,02 m/s bzw. 0,04 m/s).
- Wie groß ist die Induktionsspannung Uind bei v = 0,04 m/s?
Halbiere die Geschwindigkeit auf 0,01 m/s.
- Welche Zeit Δt benötigt die Spule bei halber Geschwindigkeit (0,01 m/s) um ins Feld zu gelangen?
- Wie verändert sich das Fläche(t)-Diagramm und die Steigung der Kurve dabei?
- Wie groß ist die Induktionsspannung Uind bei v = 0,01 m/s?
4.) Spielt die Breite d des Rähmchens eine Rolle?
Bisher hatte das Leiterrähmchen eine Grundbreite d von 0.05 m. Wird das Rähmchen breiter gemacht (0,10 m) so verändert dies auch die Fläche.
Belasse alle Grundeinstellungen (v = 0,02 m/s ;
B = 0,01 T ; n = 100)
Führe zwei Versuche aus.
Wähle als Rahmenbreite d einmal 0,05 m und einmal 0,1 m.
- Was kann man jeweils über die maximale, vom Feld durchsetzte Fläche aussagen?
- Wie groß ist also die Flächenänderung ΔA in beiden Fällen?
- Warum verändert sich dabei die Zeit Δt, in der die Fläche von 0 auf das Maximum anwächst, nicht?
- Wie verändert sich die Steigung im Fläche(t)-Diagramm?
- Welchen Einfluss hat dies auf die Induktionsspannung Uind(t)?
Etwas Theorie zum Abschluß.
Die Induktionsspannung ist zu folgenden Größen proportional:
- der Windungszahl n
- der Rahmenbreite d
- der Bewegungsgeschwindigkeit v
- der Stärke des Magnetfeldes (Flussdichte) B
Damit ergeben sich folgende Zusammenhänge:
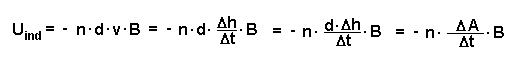
Bei gegebener Windungszahl n und gegebenem, konstanten Magnetfeld B bestimmt also die Geschwindigkeit der Flächenänderung ΔA/ Δt wie groß die Induktionsspannung Uind wird.
Diagramme helfen bei der Anschauung.
Zwei Diagramm-Ausschnitte sollen helfen dies zu veranschaulichen:
Dabei bedeutet ΔA immer Fläche zum späteren Zeitpunkt (A2) - Fläche zum früheren Zeitpunkt (A1).
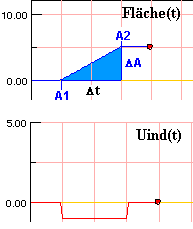 |
Die Spule wird in das Feld bewegt. Am Ende des Vorgangs ist sie A2 = 0,05 cm2, am Anfang des Vorgangs
war sie A1 = 0. Die Steigung im Fläche(t) Diagramm ist positiv. Die Induktionsspannung ist negativ. |
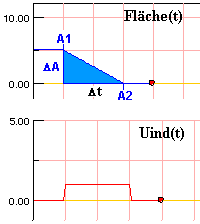 |
Die Spule wird aus dem Feld bewegt. Am Ende des Vorgangs ist A2=0, am Anfang des Vorgangs war sie
A1 = 0,05 cm2. Die Steigung im Fläche(t) Diagramm ist negativ. Die Induktionsspannung ist positiv. |
Warum in der Gleichung ein Minuszeichen steht, wird hier noch nicht so
richtig klar.
Das hat mit der Lenzschen Regel zu tun.
Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:
Sie müssen dazu die gepackte Datei (ind_bfeld.zip) herunterladen und in
ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder.
Die nötigen Java-Achive sind ebenfalls enthalten.
Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.
| Die Datei herunterladen : indbeweg_flaeche.zip |
Um den Schülerinnen und Schülern das Scrollen beim Bearbeiten der Aufgaben zu ersparen, können Sie die Fragen / Aufgaben auch hier als Arbeitsblatt (Word-Dokument) herunterladen.
| Arbeitsblatt herunterladen:
indbeweg_flaeche.doc |
Nutzungsbedingungen:
Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern
gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und
Kollegen weitergeben.
Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der
ausdrücklichen Zustimmung.
Die Simulationen entstanden mit Hilfe von Physlets
von Wolfgang Christian und Mario Belloni vom Davidson College, USA |


