Von der Drehspule zur Zeigerdarstellung.
Für die Wiedergabe der Simulationen auf dieser Seite benötigt
man die Java-Runtime-Environment. Das Laden des Applet dauert einen Augenblick. Nicht starten bevor der gelbe Kreis zu sehen ist. |
Hinweise zur Benutzung des Applets: Die Checkbox bei "Diagramm" bestimmt, ob das Diagramm gezeichnet werden soll oder nicht. Mit den Radiobuttons der ersten Zeile kann man zwischen einer
Seitenansicht der Spule und einer Ansicht mit dem Sinuspfeil (blau)
umschalten. Mit den Auswahlmenüs unter dem Applet lassen sich Amplitude, Frequenz und Startbedingung verändern. Mit Schritt kann man die Animation einen Schritt vor oder einen Schritt zurück bewegen. Eine Schrittstufe entspricht bei 25 Hz gerade einem Winkel von 5° Winkel, bei 50 Hz sind es 10°. |
Fragen und Aufgaben:
a) Die rotierende Spule als Animation.
 |
|
b) Abstraktion: es werden nur noch die Pfeile betrachtet.
Klicke nun den Radiobutton "Sinuspfeil" an.
(Der Spulenumriss wird nicht mehr gezeichnet, Du siehst aber einen gelben
Kreis, auf dem die Pfeilspitze umläuft.)
- Klicke wieder "Start" und beobachte die Bewegung des roten Pfeils.
- Beobachte auch Länge und Orientierung des blauen Pfeils.
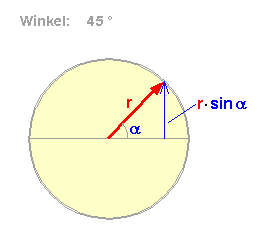
Klicke "Start" und stoppe die Animation bei einem Winkel
von 45°.
Wenn der rote Pfeil rotiert, ändert sich der Winkel zwischen der
Horizontallinie und dem Pfeil (grau eingezeichnet) ständig. |
 |
c) Der Verlauf wird im Diagramm dargestellt.
Klicke nun das Kontrollkästchen bei "Diagramm" (ganz oben links) an und starte erneut.
- Welche Kurve beschreibt den Verlauf im Diagramm?
- Wie viele Perioden sind dargestellt (bei 25 Hz)?
d) Drei gleichwertige Beschreibungsarten.
Das Diagramm kann mit unterschiedlichen Maßstabsangaben beschriftet
werden:
Die Länge des blauen Pfeils (momentane
Amplitude) kann in Abhängigkeit vom Winkel (im Gradmaß oder
im Bogenmaß) oder in Abhängigkeit von der Zeit dargestellt
werden.
Du kannst von jeder Beschriftungsart in die andere umschalten, wenn du die
Animation stoppst und bei "Beschriftung" einen anderen Radiobutton
aktivierst.
- Ergänze die folgende Tabelle:
| Gradmaß | 0° | 45° | 90° | 180° | 270° | 360° |
| Bogenmaß | 0 | |||||
| Zeitmaß | 0 |
e) Die Drehfrequenz kommt ins Spiel.
Wenn die Spule mit größerer Drehzahl rotiert (z.B. 50 Hz statt 25
Hz), dann rotiert der rote Pfeil schneller und dann ändert sich auch
sin(α(t)) schneller.
Wie kann man α(t) noch ausdrücken?
Aktiviere bei "Zeichnen" den Radiobutton
"Kreispunkt" und klicke "Start".
Stelle als Frequenz 25 Hz ein.
- Nach welcher Zeit hat der Punkt einen Viertelkreis durchlaufen?
- Bei welchem Winkel (im Gradmaß) ist er dann?
- Bei welchem Winkel (im Bogenmaß) ist er dann?
- Wie lange benötigt der Punkt um einen Halbkreis / einen ganzen Kreis zu durchlaufen?
- Welche Winkel (im Gradmaß / im Bogenmaß) entsprechen diesen Zeitpunkten?
| Du hast bestimmt gesehen, dass in doppelter Zeit auch die
doppelte Strecke auf dem Kreis zurückgelegt wird. In doppelter Zeit wird auch doppelter Winkel überstrichen. Es gilt also: s ist proportional zu t , α ist proportional zu t. |
Rotiert die Spule schneller, so bewegt sich der Punkt mit
größerer Bahngeschwindigkeit.
In der gleichen Zeit legt er dann eine größere Strecke zurück
bzw. überstreicht er einen größeren Winkel.
Es gilt also:
| Streckenbetrachtung: | Winkelbetrachtung: |
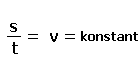 |
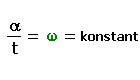 |
| v - Geschwindigkeit | ω - Winkelgeschwindigkeit |
Bei einem ganzen Umlauf wird der Winkel 2*π (Bogenmaß), bzw. der
Winkel 360° (Gradmaß) überstrichen.
Die für einen Umlauf nötige Zeit ist die Periodendauer (bzw.
Umlaufdauer) T.
Also gilt:
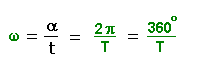
oder nach α(t) aufgelöst:
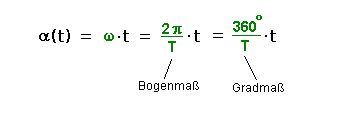
Damit ist die Länge des blauen Pfeils (die
zeitliche Änderung der Amplitude):
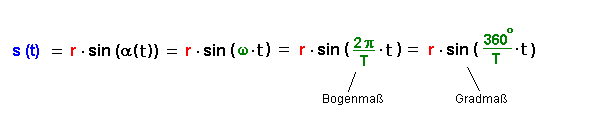
Wobei r die Länge des roten Pfeils ist. Bei unserer rotierenden Spule ist
r die halbe Spulenhöhe.
Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:
Sie müssen dazu die gepackte Datei (zeigerprinzip.zip) herunterladen
und in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder.
Die nötigen Java-Achive sind ebenfalls enthalten.
Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.
| Die Datei herunterladen : zeigerprinzip.zip ALT="gepackte Datei" BORDER="0" TITLE="gepackte Datei" HEIGHT="16" WIDTH="16"> |
Nutzungsbedingungen:
Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern
gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und
Kollegen weitergeben.
Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der
ausdrücklichen Zustimmung.
Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang
Christian und Mario Belloni vom Davidson College, USA
(Copyright Hinweise) |


