Ein virtuelles Experiment von Millikan.
Millikans Öltröpfchen-Versuch.
Für die Wiedergabe benötigt man die Java-Runtime-Environment.
Wenn Sie diese nicht haben, können Sie sie
![]() hier kostenlos
herunterladen.
hier kostenlos
herunterladen.
In den Einstellungen des Browsers muss Javascript aktiviert
sein.
0.) Welche Ladung hat ein Elektron?
Nach dem 2. Gesetz von Faraday sind 1 mol eines
Stoffes (6,02*1023 Atome) 96 500 C Ladung. Aber ist dies dann wirklich die Ladung eines Elektrons, oder ist es so etwas wie ein Mittelwert der Elektronenladung? |
 |
||
Der Amerikaner Robert A. Millikan ging 1909 dieser Frage nach, für die er 1923 den Nobelpreis bekam. Seine Überlegungen und sein Experiment kannst Du hier virtuell nachvollziehen. |
|||
Hier findest Du eine sehr gute Biografie über Robert A. Millikan und
sein Werk
![]() http://chem.ch.huji.ac.il/history/millikan.html
(englisch).
http://chem.ch.huji.ac.il/history/millikan.html
(englisch).
1.) Welche Spannung ist nötig, damit das Tröpfchen schwebt?
Sprüht man Öltröpfchen in einen Raum, so laden sich manche
Tröpfchen positiv auf, andere Tröpfchen negativ und viele bleiben
neutral. Millikan spritze die Öltröpfchen zwischen die Platten eines
Kondensators, an die er eine Spannung anlegte (vgl. Abbildung im Java-Applet).
Den kleinen Zwischenraum beobachtete er mit einem Mikroskop.
Die verschiedenen Öltröpfchen führen verschiedene Bewegungen
aus:
- neutrale Öltröpfchen fallen wegen der Schwerkraft nach
unten.
Ob eine Spannung angelegt ist oder nicht, spielt für sie keine Rolle.
- positiv geladene Öltröpfchen erfahren zusätzlich
zur Schwerkraft noch eine elektrische Kraft nach unten.
Sie werden also zur negativen Platte nach unten hin beschleunigt und verschwinden daher schnell aus dem Sichtfeld.
- auf negativ geladene Öltröpfchen wirkt die Schwerkraft
nach unten und die elektrische Kraft nach oben.
Sie fallen also langsamer. Wählt man eine geeignete Spannung, dann kann man sie sogar zum Schweben bringen.
Wählt man die Spannung zu klein, bewegen sie sich dennoch nach unten,
wählt man die Spannung zu groß, werden sie nach oben zur positiven Platte hin beschleunigt.
Für das Schweben eines Öltröpfchens gilt folgende Bedingung:
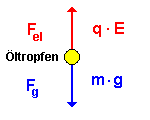 |
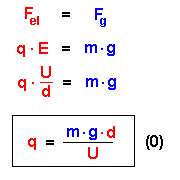 |
Durch geeignete Wahl der Spannung U kann man das Tröpfchen zum Schweben bringen.
Fragen und Aufgaben:
a) Probiere die Tröpfchen Nr. 0, Nr.1 und Nr. 2 aus.
- Welches Ladungsvorzeichen haben diese Tröpfchen? Woran merkst Du das?
b) Versuche das Tröpfchen Nr. 2 und noch vier weitere
Tröpfchen zum Schweben zu bringen.
- Lege dazu eine Tabelle in folgender Form an oder verwende die EXCEL-Tabelle, die man am Seitenende herunterladen kann, zur Auswertung.
| Tröpfchen Nr. | Spannung U | |||||
| 2 | ||||||
| ... | ||||||
| ... | ||||||
| ... | ||||||
| ... |
- Trage jeweils die Nummer des Tröpfchens ein und die Spannungen U, bei der das Tröpfchen schwebt.
Anmerkung:
In der Simulation wird davon ausgegangen, dass die Differenzkraft von
Fel und Fg die Öltröpfchen nach oben oder unten
auf der ganzen Strecke beschleunigt.
Dies wäre aber nur dann so, wenn der Raum zwischen den Platten
evakuiert ist. In Millikans Anordnung befand sich aber Luft
zwischen den Platten.
Warum dies für das Experiment wichtig ist, beschreibt der nächste
Abschnitt.
Dies wurde hier nicht berücksichtigt, damit man die Auswirkung der
Differenzkraft besser sehen kann.
2.) Bestimmung der Masse des Tröpfchens aus der Sinkgeschwindigkeit.
Wir kennen die Masse m des Tröpfchens nicht!
Leider können wir mit der Gleichung q = m * g * d / U die
Ladung eines Elektrons noch nicht so einfach bestimmen!
Zwar kennen wir die Spannung U und den Plattenabstand d sowie die
Fallbeschleunigung g, aber wir kennen die Masse des Tröpfchen
nicht!
Wir könnten höchstens die spezifische Ladung q /
m = g * d / U angeben.
Die Öltröpfchen sind in der Praxis auch zu klein, dass man ihren
Radius r einfach im Mikroskop messen könnte!
Würden wir den Radius r kennen, dann könnten wir die Masse m des
Tröpfchen bestimmen.
Die Tröpfchen sind nämlich kugelförmig und für das
Volumen V einer Kugel gilt:
V = 4/3 * π * r3
Damit erhält man die Masse m :
|
(1) |
Das Tröpfchen fällt wie ein Fallschirm...
Um die Masse zu bestimmen, gibt es jedoch folgende Möglichkeit:
Wir nehmen die Spannung an den Kondensatorplatten weg und lassen das
Öltröpfchen fallen.
Ähnlich wie beim Fallschirm, wird das Tröpfchen zunächst eine
kleine Strecke beschleunigt.
Dabei baut sich ein Luftwiderstand auf, der dieser Beschleunigung entgegen
wirkt. Nach kurzer Zeit stellt sich ein Kräftegleichgewicht zwischen der
Schwerkraft (nach unten) und der Luftwiderstandskraft (nach oben) ein - der
Tropfen fällt dann mit konstanter Geschwindigkeit.
(Von der Beschleunigungsphase sehen wir hier in der Simulation ab.)
![]() vgl. hierzu auch folgende Seite auf dem
Landesbildungsserver (Freier Fall mit Luft).
vgl. hierzu auch folgende Seite auf dem
Landesbildungsserver (Freier Fall mit Luft).
Es gilt dabei:
| nach oben | nach unten | |
| Luftwiderstand (Stokes) | Schwerkraft | |
| FL | = | Fg |
| 6 π * r * η* v | = | m * g |
Dabei ist η die Zähigkeit der Luft, sie ist etwa 1,8*10-5 N*s / m2
Setzen wir die Dichte von Öl und das Kugelvolumen V von oben (Gleichung
1) in diese Gleichung ein, so erhalten wir:
6 π * r * η* v = ρ * 4/3 * π * r3 *
g
Durch π und r dividiert, etwas gekürzt und nach r2
aufgelöst folgt dann weiter:
|
(2) |
Wenn wir also die Fallgeschwindigkeit v bestimmen, können wir den Tröpfchenradius r berechnen und dann mit Hilfe der Dichte von Öl die Masse m des Tröpfchens m bestimmen. Damit bekommen wir dann schließlich heraus, welche Ladung q das Tröpfchen trägt.
Fragen und Aufgaben.
Bestimme für alle negativ geladenen Tröpfchen, die Du im Applet oben untersucht hast, hier die Sinkzeit t und ergänze die Tabelle entsprechend.
- Bestimme damit für alle Tröpfchen die Fallgeschwindigkeit v = s / t. Die Fallstrecke s ist 3 mm.
- Bestimme mit Hilfe der Gleichung (2) die Radien der Tröpfchen.
- Bestimme mit Hilfe der Gleichung (1) die Massen der Tröpfchen.
- Ermittle schließlich mit Gleichung (0) ihre Ladung.
| Tropfen Nr. | Spannung U | Sinkzeit t | Geschwindigkeit v | Radius r | Masse m | Ladung q |
| 2 | ||||||
| ... | ||||||
| .... | ||||||
| ... | ||||||
| ... |
Weitere Materialien zur Seite:
Hier gibt es ein Arbeitsblatt zum Auswerten:
millikan.pdf ![]() ( 137 kB )
( 137 kB )
Wenn Du möchtest, kannst Du hier ein interaktives Auswertungsblatt in
EXCEL herunterladen, das Dir beim Rechnen (und Umrechnen der Einheiten hilft):
millikan.xls ![]() ( 17 kB )
( 17 kB )
| Anmerkung: | Im Allgemeinen haben die Tröpfchen natürlich völlig unterschiedliche Massen. In dieser Simulation kommen aber nur drei verschiedene Tröpfchenmassen vor. |
Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang
Christian und Mario Belloni |


