Die Energie einer stromdurchflossenen Spule.

Herleitung mit Hilfe der Exponentialfunktionen.

1.) Überraschung beim Ausschaltvorgang.

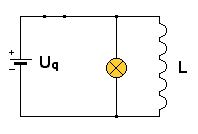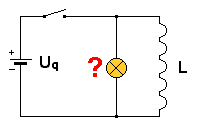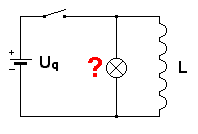Eine Glühlampe 3,8 V, 70 mA ist einer Induktionsspule parallelgeschaltet. (vgl. Skizze). Zunächst ist der Schalter geschlossen. Die Spule hat 1000 Windungen und einen geschlossenen Eisenkern. -> Was wird passieren, wenn der Schalter geöffnet wird? Wahrscheinlich erwartest du, dass nach dem Öffnen des Schalters die Glühlampe noch eine Zeit lang weiterleuchtet und dann ausgeht. (Lenz'sche Regel)

Tatsächlich passiert aber das, was du hier im Film sehen kannst

Die Lampe blitzt nur kurz auf und ist dann durchgebrannt. Bei zweiten Öffnen erkennst du einen kleinen Lichtbogen am Schalter.

2.) Wo kommt die Energie für die Zerstörung der Lampe her?

Die Energie kann nicht direkt aus der Quelle stammen, denn diese wird ja beim Öffnen des Schalters abgetrennt.
Außer der Lampe ist die Spule das einzige Bauteil im Stromkreis, nur sie kommt also als Energiequelle in Frage.
Eine stromdurchflossene Spule hat Energie gespeichert.

Vor dem Ausschalten war die Spule von einem Magnetfeld durchsetzt. Nach dem Öffnen des Schalters fehlt die Quelle, die den Stromfluss in der Spule langfristig aufrecht erhalten kann. Das Magnetfeld wird abgebaut.
Die in diesem Feld gespeicherte Energie muss nach dem Energieerhaltungssatz irgendwo bleiben: hier sorgt sie für die Zerstörung der Lampe, oder entlädt sich beim zweiten Öffnen des Schalters in einem kleinen Lichtbogen am Schalter.
Das sich ändernde Magnetfeld sorgt für eine Selbstinduktionsspannung und einen Induktionsstrom.

3.) Selbstinduktionsspannung und Induktionsstrom.

Auf diesen Seiten wurde hergeleitet, wie man den Verlauf der Selbstinduktion beim Ausschaltvorgang mit Hilfe von Exponentialfunktionen beschreiben kann:

• Exakte Gleichungen für die Selbstinduktion beim Ausschalten.
• Entladen eines Kondensators und Selbstinduktion beim Ausschalten - ein Vergleich.

Die Funktionen und ihr Verlauf sind hier noch einmal kurz zusammengestellt
(R ist der Gesamtwiderstand - also die Summe aus Spulenwiderstand R_sp und dem Widerstand der Lampe R_La):

	Funktionsgleichung	Diagramm
Selbstinduktionsspannung Uind(t)
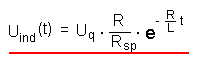
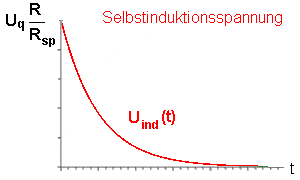Stromstärke I(t)

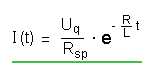4.) Elektrische Leistung und elektrische Energie.

Wir übertragen unsere Kenntnisse über die elektrische Leistung P und die elektrische Energie W auf unser Problem:

	Mittelstufe	Selbstinduktion
elektrische Leistung P(t)
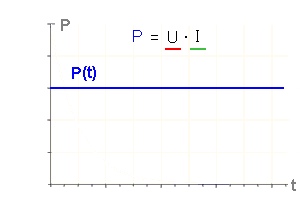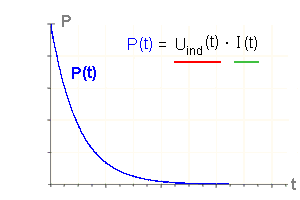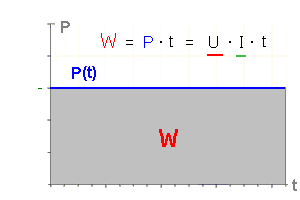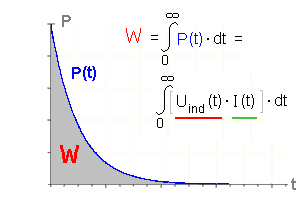elektrische Energie W(t)	Die elektrische Energie ist die Fläche unter der Kurve im P-t-Diagramm.	Die elektrische Energie ist die Fläche unter der Kurve im P-t-Diagramm. Wir müssen also das Integral bilden.

Für die in der Spule gespeicherte elektrische Energie gilt also:

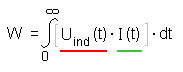
wir setzen die Ausdrücke für die Selbstinduktionsspannung (rot) und die Stromstärke (grün) von oben ein:

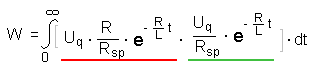
und fassen noch etwas zusammen, es ergeben sich zwei gleiche Exponentialausdrücke (lila):

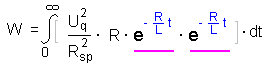
Wir wenden nun die Potenzgesetze an.
Wir multiplizieren hier zwei gleiche Ausdrücke, also ist n = 2:

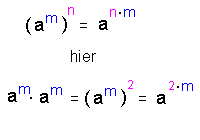
Es folgt damit für die Energie der Spule:

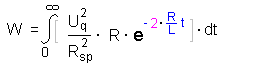
Für den nächsten Schritt färben wir die Faktoren etwas anders ein:

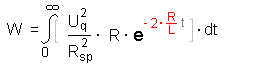
Um das Integral zu lösen müssen wir die Stammfunktion der Exponentialfunktion suchen.
Dabei gelten folgende Beziehungen:

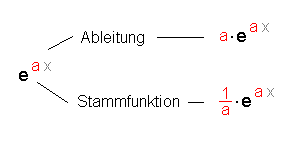
Die rot zusammengefassten Größen entsprechen dem Faktor a, die Zeit t dem Faktor x.
Wir kommen daher zu folgender Beziehung (der Gesamtwiderstand R kann noch gekürzt werden):

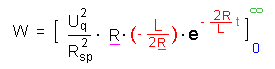
Die obere Grenze minus die untere Grenze eingesetzt ergibt dann
(e hoch minus unendlich ist 0 ; e hoch 0 ist 1):

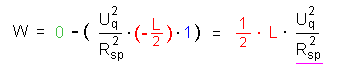
Wir können das noch etwas umschreiben, wenn wir die Stromstärke in der Spule direkt vor dem Ausschalten (I₀) verwenden.
Diese ist nämlich:

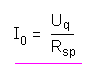
Also folgt nun:

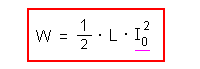
5.) Eine bekannte Bauform von Energiegleichungen.

Die Gleichung ist auch leicht zu merken, denn er gibt zahlreiche Energiegleichungen, die dieselbe Bauform haben.

Energieform	Formel
kinetische Energie
Energie in einer Spule
Energie in einem Kondensator
Energie einer gespannten Feder

6.) Ein Rechenbeispiel zum Schluss.

Welche Energie ist im Magnetfeld einer Spule gespeichert, die eine Eigeninduktivität von 0,5 H hat und von einem Strom von 2,0 A durchflossen wird?

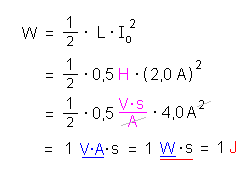
Grüninger, Landesbildungsserver, 2016