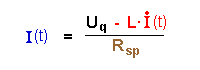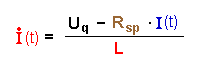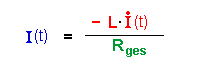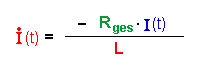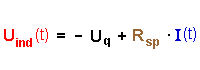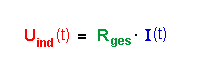Übericht: Selbstinduktion beim Ein- und Auschalten.
Unterschiedliche Ersatzschaltbilder - unterschiedliche Theorien:
| Einschalten: | Ausschalten: |
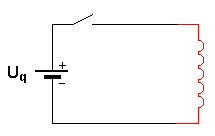
| Grundschaltung: | |
 |
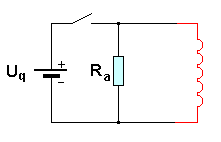 |
| Für den Stromfluss in der Spule ist es unerheblich, ob parallel zur Spule noch Strom durch einen zweiten Widerstand fließt. | Wenn der Schalter geöffnet ist, ist die Quelle nicht mehr mit der Spule verbunden. Ein Strom kann nur noch durch den Widerstand Ra fließen. |
| Ersatzschaltbild: | |
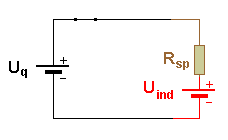 |
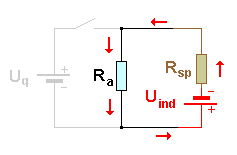 |
| Uind ist umgekehrt gepolt wie
Uq. Die Induktion arbeitet der Quelle und dem Ansteigen der Stromstärke entgegen. |
Uind und Uq sind gleich gepolt. Nach dem Öffnen des Schalters übernimmt die Induktionsspannung die Rolle der Quelle und sorgt dafür, dass der Stromfluss noch eine Zeit lang erhalten bleibt. |
| Ersatzschaltbild weiter entwickelt: | |
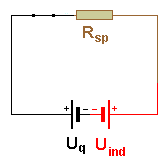 |
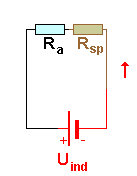 |
| Hier entscheidet die Gesamtspannung aus zwei
Quellen, wie groß die Stromstärke an einem Widerstand
Rsp werden kann. Uind(t) arbeitet der Quelle Uq entgegen. |
Hier gibt es nur eine Quelle :die Induktionsspannung.
Beide Widerstände zusammen entscheiden, wie groß die Stromstärke und die Stromstärkeänderung werden. Uind(t) übernimmt die Rolle der Quelle ist also gleich gepolt wie Uq. |
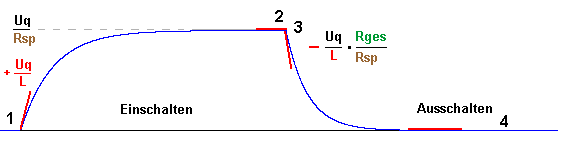
Verlauf der Stromstärke und der Stromstärkeänderung: |
|||
 |
|||
Einschalten: |
Ausschalten: |
||
| t = 0 s (1) | t = ∞ (2) | t = 0 s (3) | t = ∞ (4) |
Stromstärke: |
|||
| Ganz zu Beginn ist die Stromstärke 0: I(t=0s) = 0. |
Nach sehr langer Zeit gibt es keine Selbstinduktion mehr. Der zweite Ausdruck fällt weg. Die Stromstärke geht gegen den Endwert I(t=∞) = Uq / Rsp |
Ganz zu Beginn ist die Stromstärke so wie sie vor dem
Ausschalten war, also I(t=0s) = Uq / Rsp. |
Nach sehr langer Zeit gibt es keine Selbstinduktion mehr. Die
Induktionsspannung (Zähler) wird dann 0. Also ist I(t=∞) = 0. |
Änderung der Stromstärke (Steigung): |
|||
| Da I(t=0s) = 0 fällt der zweite Ausdruck im
Zähler weg. Also steigt die Stromstärke zunächst mit + Uq / L |
Da
I(t=∞) = Uq / Rsp, wird der
zweite Ausdruck im Zähler gleich Uq, d.h. der Zähler
insgesamt 0. Die Stromstärke steigt nicht weiter an. |
Da
I(t=0s) = Uq / Rsp ergibt sich
für die Änderung der Stromstärke ganz zu Beginn: - Uq / L * Rges / Rsp |
Wenn I(t=∞) = 0, dann ist der Zähler
0. Die Stromstärke fällt also nicht mehr weiter ab. |
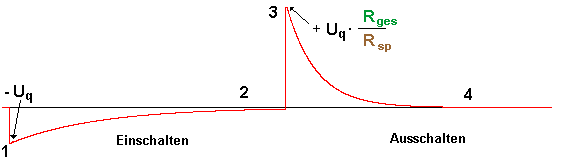
Verlauf der Induktionsspannung: |
|||
 |
|||
Einschalten: |
Ausschalten: |
||
| t = 0 s (1) | t = ∞ (2) | t = 0 s (3) | t = ∞ (4) |
| Da I(t=0s) = 0 fällt der zweite
Ausdruck weg. Im ersten Augenblick ist also Uind = -Uq, d.h. die Induktionsspannung kompensiert die Quelle ganz. (Uges = 0) |
Nach langer Zeit ist I(t=∞) = Uq / Rsp. Der zweite Faktor wird also + Uq. Daher wird Uind(∞) = 0. |
Da die Stromstärke zu Beginn
I(t=0s) = Uq / Rsp ist also die
Induktionsspannung Uind(0) = + Uq * Rges / Rsp |
Nach langer Zeit ist
I(t=∞) = 0 also wird auch die Induktionsspannung Uind(∞) = 0 |
Grüninger, Landesbildungsserver, 2004