Selbstinduktion beim Ausschalten.
1.) Ein überraschender Anfang.
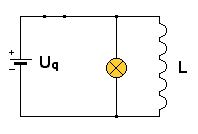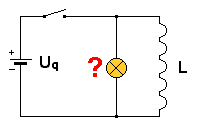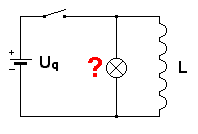 |
Eine Glühlampe 3,8 V, 70 mA ist einer Induktionsspule parallelgeschaltet. (vgl. Skizze). Zunächst ist der Schalter geschlossen. Die Spule hat 1000 Windungen und einen geschlossenen Eisenkern. -> Was wird passieren, wenn der Schalter geöffnet wird? Wahrscheinlich erwartest du, dass nach dem Öffnen des Schalters die Glühlampe noch eine Zeit lang weiterleuchtet und dann ausgeht. (Lenz'sche Regel) |
Schau dir an, was tatsächlich passiert!
-> Beim Ausschalten leuchtet die Glühlampe
überraschenderweise nur kurz hell auf und ist dann
"durchgebrannt".
Beim nächsten Schließen des Schalters leuchtet die Lampe nicht
mehr.
Beachte auch den "Abrißfunken" am Schalter kurz vor Ende des
Videos!
1) Wo kommt die Energie für die Zerstörung der Lampe her?
Es kann nur die Energie sein, die vor dem Öffnen des Schalters im Magnetfeld der Spule gespeichert war, denn nach dem Öffnen des Schalters ist die Lampe ja nicht mehr mit der Quelle verbunden, die Energie muss also aus der Spule stammen.
2) Warum brennt die Lampe durch?
- Wie kann es sein, dass eine Induktionsspannung entstehen kann, die offenbar größer als die Spannung der Quelle ist?
- Wie groß kann diese Spannung eigentlich werden?
- Wie ist diese Spannung gepolt?
2.) Die Glimmlampe bringt Gewissheit und wirft neue Fragen auf.
Zur Beantwortung dieser Fragen machen wir einen weiteren Versuch, in dem wir die Glühlampe durch eine Glimmlampe ersetzen. Zuvor stellen wir folgende Eigenschaften der Glimmlampe fest:
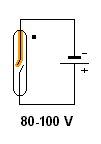 |
|
Sieh dir den folgenden Versuch (falls nötig in "Zeitlupe")
an.
Beachte: die Glimmlampe leuchtet immer dann auf, wenn der Schalter
geöffnet wird.
Wir müssen zwei Phasen des Versuchs unterscheiden:
Der Schalter ist geschlossen:
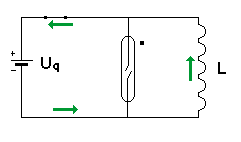 |
Die Spannung der Quelle von etwa 4 V ist viel zu klein um die Glimmlampe
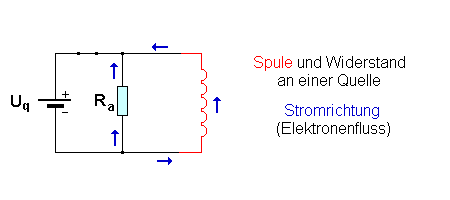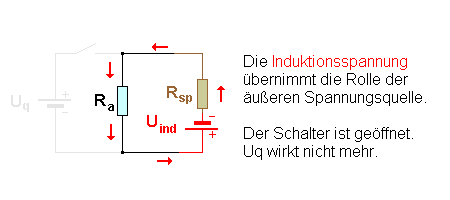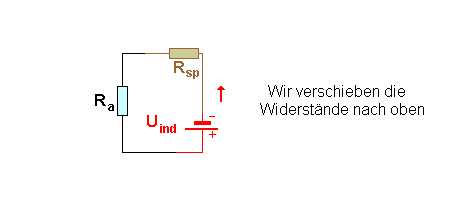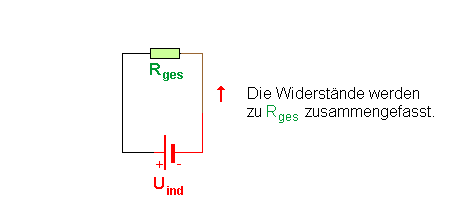
zu zünden, sie leuchtet daher nicht. Vor dem Öffnen des Schalters ergibt sich lediglich ein Strom durch die Spule in der eingezeichneten Richtung. (die Pfeile geben die Richtung an, in der sich die Elektronen bewegen.) |
Der Schalter wird geöffnet, jetzt ist nur noch der rot umrandete Teil wirksam.
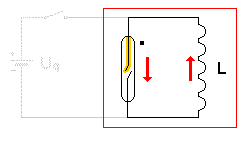 |
Nach dem Öffnen des Schalters soll der Stromfluß in der Spule
unterbrochen werden. Die Stromstärke I, die Flussdichte B und der
magnetische Fluss F sollten abnehmen. (DI / Dt bzw DF / Dt sind also negativ.) Nach Lenz muss also eine Spannung so induziert werden, dass der Induktionsstrom diese Abnahme bremst und den bisherigen Stromfluss möglichst aufrecht erhält. (Dahinter steckt letztlich der Energieerhaltungssatz : die Energie in der Spule kann nicht plötzlich verschwinden!) Die Stromrichtung bleibt also gleich. Der Betrag der Stromstärke ist im ersten Augenblick so groß wie vor dem Ausschalten. Vom oberen Ende der Spule gehen also Elektronen aus, dort ist der -Pol der Induktionsspannung. Daher leuchtet der obere Teil der Glimmlampe auf. |
-> Wie kann die Induktionsspannung tatsächlich 100 V oder mehr betragen, wie groß kann sie werden und wovon hängt dies ab?
3.) Theorie der Induktion beim Ausschalten.
....ersetzt und um die Ecke gedacht......
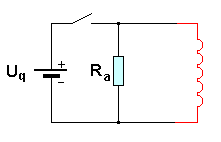
Wenn der Schalter geöffnet ist, kann die Spule wieder durch den Spulenwiderstand Rsp und die Induktionsspannung Uind(t) ersetzt werden.
 |
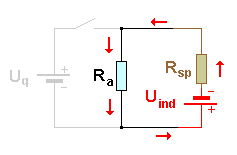 |
Beachte die Parallele zur Darstellung mit der Glimmlampe oben.
Die Induktionsspannung ist in derselben Richtung gepolt wie die Quelle Uq. Dies muss auch so sein, damit der Stromfluss in der Spule zunächst noch in derselben Richtung aufrecht erhalten werden kann.
Schau dir an, welche Vereinfachungen man weiter machen kann, die in die Theorie eingehen:
Es ergeben sich damit folgende Beziehungen (Uq ist dabei die Spannung der Quelle):
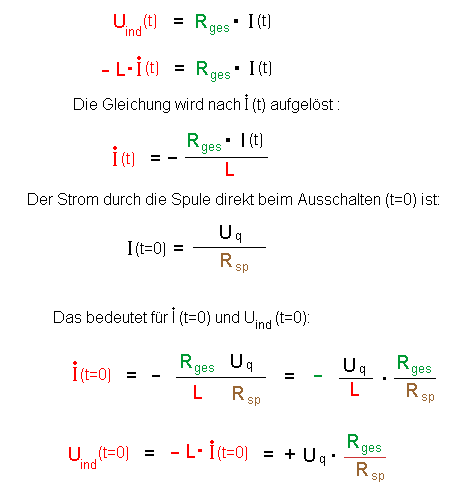
4.) Diskussion der einzelnen Anteile.
a) Zunächst steht da ein "+" : d.h. die Induktionsspannung ist gleich gepolt wie die äußere Spannungsquelle. Das muss sie ja auch sein, denn der Stromfluss soll ja beim Auschalten in derselben Richtung erhalten bleiben (Lenz).
b) es folgt die Spannung der Quelle Uq multipliziert mit einem Faktor Rges / Rsp
Grenzfälle:
- ist Ra >> Rsp (wie es z.B. bei der
Glimmlampe der Fall ist), dann ist auch Rges >>
Rsp.
In diesem Fall wird die Induktionsspannung beim Ausschalten "riesig groß".
Sie reicht für das Zünden den Glimmlampe aus.
- ist Ra = 0, (d.h. die Glühlampe, die
parallel zur Spule liegt, hätte gar keinen Widerstand), dann wäre
Rges = Rsp.
Der Widerstandsfaktor wäre 1 und die Induktionsspannung gleich der Spannung der Quelle.
- nun ist der Widerstand der Glühlampe sicher größer als 0
aber kleiner als unenendlich.
Der Widerstandsfaktor wird also größer als 1 sein, d.h. die Induktionsspannung wird größer als die Spannung der Quelle.
5.) Ein Beispiel zum Schluß ...... und worauf man achten muss.
Aber nun zurück zu unserer Frage vom Anfang:
-> Wie groß war die Induktionsspannung wirklich, welche die Lampe beim Ausschalten zerstört hat?
a)
Unterstellen wir einmal, dass der Widerstand der Glühlampe konstant sei:
also Ra = 3,8 V / 0,07 A = 54,28 Ohm.
Der Spulenwiderstand Rsp möge 10 Ohm betragen. Dann ist der Gesamtwiderstand Rges = Ra + Rsp = 64,28 Ohm.
Der Widerstandsfaktor wird dann: Rges / Rsp = 64,28 Ohm / 10 Ohm = 6,4.
Bei einer Spannung der Quelle von Uq = 4V wäre die Induktionsspannung ganz zu Beginn also 4V * 6,4 = 25,6 V.
b)
Ganz richtig ist diese Betrachtung nicht, denn wenn der Glühlampenfaden
kalt ist, ist sein Widerstand geringer. Auch beim "Durchbrennen" der
Lampe muss sich der Glühfaden zunächst erwärmen!
Selbst wenn der Widerstand der Glühlampe im kalten Zustand nur
Ra = 20 Ohm wäre, dann wäre
Rges = 30 Ohm und der Faktor 3.
Die Induktionsspannung ganz zu Beginn des Ausschaltvorgangs wäre dann 3*4
V = 12 V, was die Glühlampe wahrscheinlich nicht
"überlebt".
Soll der Versuch also "gelingen" (sprich: die Glühlampe
zerstört werden !) dann darf der Widerstand der Glühlampe im kalten
Zustand nicht zu klein sein.
Eine Überlastung um einen Faktor 2 halten Glühlampen meist noch aus!
Der "Kaltwiderstand" der Lampe also sollte mindestens doppelt so
groß (besser 3 mal so groß) wie der Spulenwiderstand sein, damit
der Versuch "gelingt".
Simulationen zur Selbstinduktion beim Ausschalten:
| mit Crocodile Physics : | /unterricht/faecher/physik/modell/crocodile/*.cyp |
| mit Easysim : | ind_mit_easysim.htm |
| mit Excel : | Selbstinduktion beim Ausschalten mit EXCEL |
| Direkt zur Datei | Direkt zur Datei |
Weiterführende Seiten zur Selbstinduktion:
| Exakte Gleichungen : Selbstinduktion beim Ausschalten |
| Zusammenfassung : Selbstinduktion |
| Selbstinduktion beim Einschalten |
| Exakte Gleichungen : Selbstinduktion beim Einschalten |
© Text, alle Filme und Grafiken, Grüninger, Landesbildungsserver


