Exakte Gleichungen für die Selbstinduktion beim Ausschalten.

Möchte man den Verlauf der Stromstärke und der Induktionsspannung genauer untersuchen, wird man meist auf Simulationsverfahren (Crocodile Physics, Modellbildungssysteme, Excel, usw.) zurückgreifen, die das Problem über ein Iterationsverfahren lösen.

Als mathematische Grundlagen für eine geschlossene Behandlung der Vorgänge bei der Kondensatorladung und Induktion bräuchte man die Lösung der Differentialgleichung erster Ordnung und die Exponentialfunktion.
Diese sind bis zu dem Zeitpunkt, zu dem die Physik sie bräuchte, leider meist noch nicht im Mathematikunterricht behandelt worden.

1.) Die Intuition hilft weiter.

Hat man das Vorgehen bei den exakten Gleichungen für die Selbstinduktion beim Einschalten verstanden, lassen sich recht intuitiv auch die entsprechenden Gleichungen für die Selbstinduktion beim Ausschalten finden.

• Ganz zu Beginn des Ausschaltvorgangs (t = 0 s) hat die Stromstärke genau den Wert, den sie nach sehr langer Zeit am Ende des Einschaltvorgangs erreicht hat, also U_q / R_sp.
• Die Stromstärke fällt anschließend exponentiell ab, d.h. auch hier wird es wieder eine e^-at Funktion geben.
  
  
• Zum Zeitpunkt t = 0 s ist deren Wert wieder 1.
  
  
• Für das Abfallen der Stromstärke ist aber nun nicht nur der Spulenwiderstand R_sp verantwortlich, sondern es hängt auch noch von dem äußeren Widerstand R_a ab. Ihre Summe bestimmt als R_ges zusammen, wie schnell die Stromstärke abnimmt.
  (vgl. hierzu die Seite "Selbstinduktion beim Ausschalten".)

Folgender Ansatz ist also naheliegend:

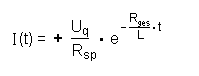
2.) Die Änderung der Stromstärke.

Die Änderung der Stromstärke ist die Ableitung der I(t) - Funktion nach der Zeit t. Man muss also wissen, wie man eine Exponentialfunktion e^x ableitet.
Im Mathematikunterricht lernt man folgenden Zusammenhang, den man auch in einer Formelsammlung finden kann:

Damit folgt dann für die Änderung der Stromstärke:

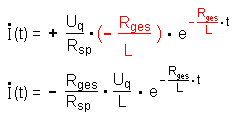
Hier stammt der Faktor, der zunächst in der Klammer steht, wieder von der Kettenregel.
Danach werden die beiden Vorfaktoren umgruppiert und die Widerstände zu einem Faktor R_ges / R_sp zusammengefasst.

Probe mit den Extremwerten, ob dies sinnvoll ist:

t = 0 s : dann wird der Exponentialfaktor e-Rsp*0 / L = 1. Insgesamt ergibt sich dann der nebenstehende Ausdruck. Die Stromstärke nimmt ab ("-" Zeichen). Sie tut dies mit dem Faktor Uq / L. Bis auf das Vorzeichen ist dies genau wie bei der Induktion beim Einschalten. Jedoch kommt nun noch zusätzlich der Faktor Rges / Rsp ins Spiel : je größer der äußere Widerstand ist (d.h. je größer auch Rges wird), desto schneller fällt die Stromstärke ab.

t ® ¥ : dann geht der Exponentialausdruck gegen 0 und die Stromstärkeänderung strebt gegen 0.

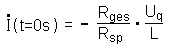3.) Die Induktionsspannung beim Ausschalten:

Für die Induktionsspannung ergibt sich dann:

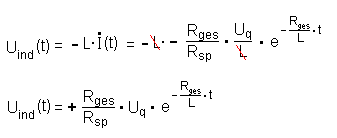
Betrachtung mit den Extremwerten :

t = 0 s : dann wird der Exponentialfaktor e-Rsp*0 / L = 1. Insgesamt ergibt sich dann der nebenstehende Ausdruck. Die Induktionsspannung ist positiv ("+" Zeichen), sie ist also gleich gepolt, wie die Spannung der Quelle Uq. Jedoch kommt nun noch zusätzlich der Faktor Rges / Rsp ins Spiel : je größer der äußere Widerstand ist (d.h. je größer auch Rges wird), desto größer wird die Induktionsspannung ganz zu Beginn.

t ® ¥ : dann geht der Exponentialausdruck gegen 0 und die Selbstinduktionsspannung strebt gegen 0.

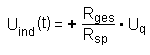4.) Die Ansatzprobe des oben behaupteten Ansatzes:

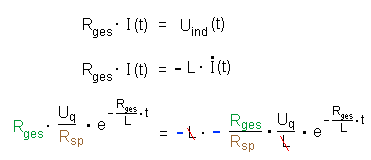
5.) Zusammenfassung:

Für die Selbstinduktion beim Ausschalten gelten also folgende exakte Gleichungen:

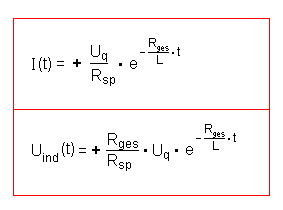
Verwandte Seiten:

Grüninger, Landesbildungsserver