Selbstinduktion beim Einschalten.
1.) Ein Strom, der zu spät kommt.
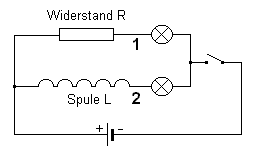 |
In einem Stromkreis sind zwei Glühlämpchen 3,8V; 70 mA
parallelgeschaltet. |
Beide Teilstromkreise werden durch einen Schalter gleichzeitig mit der Quelle verbunden.
Schau dir im Film an was passiert.
Während die Lampe im Teilstromkreis mit dem ohmschen Widerstand sofort
aufleuchtet, leuchtet die Lampe mit der vorgeschalteten Spule verzögert
auf.
->Warum passiert dies?
2.) Die Spule induziert sich selbst.
Steigt beim Einschalten die Stromstärke in der Spule an, so baut sich ein Magnetfeld B auf. Die magnetische Flussdichte B und der magnetische FlussF nehmen zu.
Dieser sich ändernde Fluss kann nun nicht nur in einer anderen Spule eine Induktionsspannung erzeugen, sondern auch in der felderzeugenden Spule selbst. Man nennt dies Selbstinduktion, die erzeugte Spannung Selbstinduktionsspannung Uind.
Es gilt:
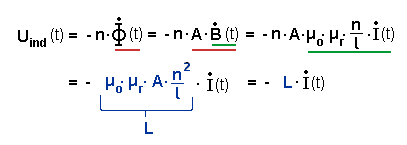
Die Größe L heißt Eigeninduktivität.. Sie ist die Kenngröße einer Spule, so wie die Kapazität die Kenngröße eines Kondensators ist.
Es gilt offenbar auch:
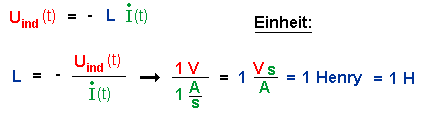
3.) Theorie zur Induktionsspannung und zum Induktionsstrom beim Einschalten.
....ersetzt und um die Ecke gedacht......
Die Glühlampe wurde für die folgende Betrachtung weggelassen, sie diente im Versuch oben nur als Nachweisinstrument für den Stromfluss, ist für die Induktion aber nicht wichtig.
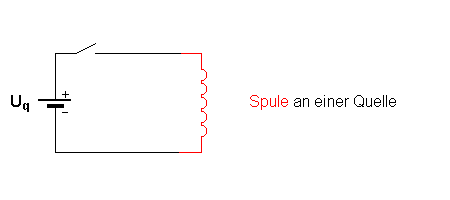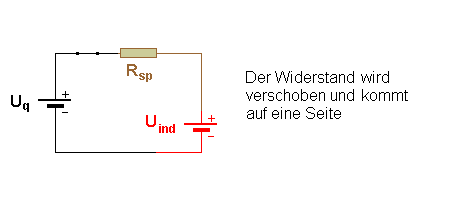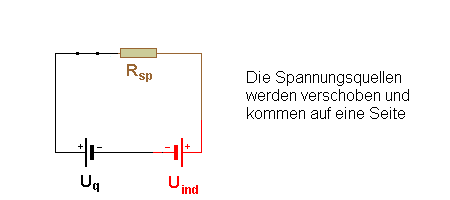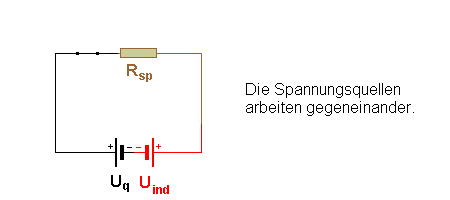
Die beiden Spannungsquellen, die konstante Spannung Uq der
Quelle, und die veränderliche Induktionsspannung Uind(t)
arbeiten gegeneinander.
Uind(t) kann dabei maximal so groß wie Uq werden,
es ist also Uq ³ Uind(t) bzw. Uges
³ 0.
Für die Spannungen und die Stromstärke I(t) im Stromkreis ergeben sich also:
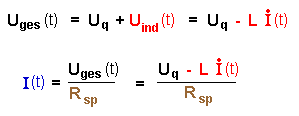
Etwas umgeformt folgt daraus für die Anstiegsgeschwindigkeit der Stromstärke:
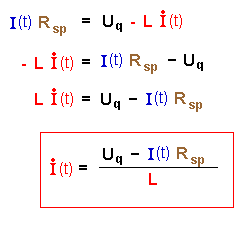
bzw. für den Verlauf der Induktionsspannung Uind(t) :
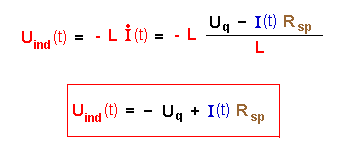
Simulationen zur Selbstinduktion beim Einschalten:
| mit Crocodile Physics : /unterricht/faecher/physik/modell/crocodile/*.cyp |
| mit Easysim : ind_mit_easysim.htm |
| mit Excel : Selbstinduktion beim Einschalten mit EXCEL |
Weiterführende Seiten zur Selbstinduktion:
| Exakte Gleichungen : Selbstinduktion beim Einschalten |
| Zusammenfassung : Selbstinduktion |
| Selbstinduktion beim Ausschalten |
| Exakte Gleichungen : Selbstinduktion beim Ausschalten |
© Text, alle Filme und Grafiken, Grüninger, Landesbildungsserver


