Exakte Gleichungen für die Selbstinduktion beim Einschalten.
Möchte man den Verlauf der Stromstärke und der Induktionsspannung genauer untersuchen, wird man meist auf Simulationsverfahren (Crocodile Physics, Modellbildungssysteme, Excel, usw.) zurückgreifen, die das Problem über ein Iterationsverfahren lösen.
Als mathematische Grundlagen für eine geschlossene Behandlung der
Vorgänge bei der Kondensatorladung und Induktion bräuchte man die
Lösung der Differentialgleichung erster Ordnung und die
Exponentialfunktion.
Diese sind bis zu dem Zeitpunkt, zu dem die Physik sie bräuchte, leider
meist noch nicht im Mathematikunterricht behandelt worden.
1.) Ein Lösungsversuch für I(t).
Behauptung : Für die Stromstärke I(t) gilt folgende exakte Funktion:
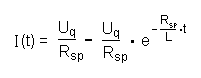
Probe mit den Extremwerten:
|
dann wird nach Definition e-Rsp*t / L = 1, damit wird I(t=0) = 0. |
|
dann geht der Exponentialausdruck gegen 0 und I(t) strebt gegen den Grenzwert I (t = ∞) = Uq / Rsp. |
2.) Die Änderung der Stromstärke.
Die Änderung der Stromstärke ist die Ableitung der I(t) - Funktion
nach der Zeit t. Man muss also wissen, wie man eine Exponentialfunktion
ex ableitet.
Im Mathematikunterricht lernt man folgenden Zusammenhang, den man auch in einer
Formelsammlung finden kann:
|
Damit folgt dann für die Änderung der Stromstärke:
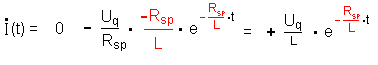
Der erste Faktor ist konstant und unabhängig von der Zeit t und
fällt daher beim Ableiten weg.
Der Vorfaktor kommt von der Kettenregel.
(der rot gefärbte Ausdruck entspricht also
"a").
Der Spulenwiderstand Rsp kürzt sich im Vorfaktor weg. Das
Vorzeichen wird positiv ( "-" mal "-" ).
Probe mit den Extremwerten, ob dies sinnvoll ist:
|
|
3.) Die Induktionsspannung beim Einschalten:
Für die Induktionsspannung ergibt sich dann:
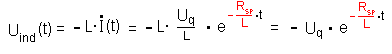
- t = 0 s: der Exponentialfaktor e-Rsp*0 / L
ist 1 : die Induktionsspannung ganz zu Beginn
ist -Uq. - t ⇒ ∞ der Exponentialausdruck geht gegen 0 und die
Induktionsspannung strebt ebenfalls gegen 0.
.
4.) Die Ansatzprobe des oben behaupteten Ansatzes:
Die Stromstärke im Widerstand der Spule ergibt sich aus der Spannung
der Quelle und der Induktionsspannung
( Differentialgleichung 1. Ordnung ).
Wir setzen in diesen Ansatz die oben gefundenen Gleichungen ein und kürzen entsprechend.
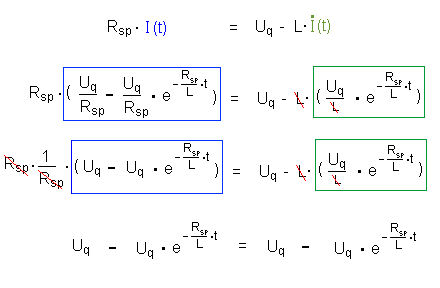
Links und rechts des Gleichheitszeichens steht dasselbe. Die oben angegebene Funktion für I(t) ist also Lösungsfunktion der Differentialgleichung.
5.) Zusammenfassung:
Für die Selbstinduktion beim Einschalten gelten also folgende exakte Gleichungen:
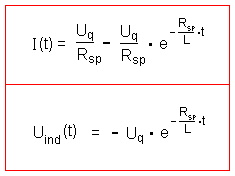
Verwandte Seiten:
| Selbstinduktion beim Einschalten (Film Experiment und Theorie) |
| Exakte Gleichungen Selbstinduktion beim Ausschalten |
| Zusammenfassung Selbstinduktion |
Grüninger, Landesbildungsserver


