Selbstinduktion beim Ein- und Ausschalten - ein virtuelles Experiment.
- Hier wird zunächst das Realexperiment vorgestellt, mit dem man den Verlauf der Induktionsspannung und der Stromstärke auf einem Oszilloskop sichtbar machen kann.
- Es folgt ein virtuelles Experiment, in dem du erforschen kannst, wie sich die Oszillogramme ändern, wenn man die Größen der Bauteile verändert.
- Den Abschluss bilden Oszilloskop-Photos aus Realexperimenten, die man mit den Darstellungen der Simulation vergleichen kann.
0.) Das Realexperiment zum Verlauf von Stromstärke und Spannung bei der Selbstinduktion.
 |
Mit dem im Photo abgebildeten Aufbau eines Realexperiments kann man den
Verlauf von Stromstärke und Spannung der Selbsinduktion beim Ein- und
Ausschalten sichtbar machen. Der gelbe Funktionsgenerator steuert mit ca. 20 Hz ein Relais (Mitte hinten) an, das Spule und Parallelwiderstand mit einer Spannungsquelle (grau, über dem Funktionsgenerator) verbindet oder von ihr trennt. |
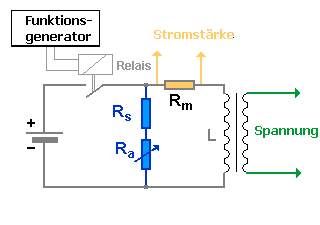 |
Hier ist das Schaltbild des im Photo gezeigten Experiments.
Die Farben im Schaltbild entsprechen den Kabelfarben im Photo. Am Messwiderstand Rm (1 Ohm) wird eine Spannung abgegriffen, die
proportional zur Stromstärke in der Spule L
ist. Diese Spannung wird einem Kanal des Zweikanaloszilloskops
zugeführt. |
1.) Das virtuelle Experiment zum Versuchsaufbau.
Der "Versuchsaufbau" entspricht dem Schaltbild oben. Rechts
erkennt man die reale Spule, bestehend aus einer idealen Spule (unten) und dem
Widerstand des Spulendrahtes Rsp (oben).
Die Widerstand des Spulendrahtes ist fest vorgegeben (9 Ohm), die
Eigeninduktivität L kann aber verändert werden. Oben erkennt man den
Messwiderstand Rm.
Parallel zur Spule liegt der Außenwiderstand
Ra. Er entspricht der Hintereinanderschaltung von
Ra und Rs.
Ra kann verändert werden, die Funktion von Rs lernst
du noch kennen!
Die Spannung der Quelle beträgt fest 10 V.
Bitte warten, bis die Animation vollständig geladen
ist.
Der Schaltplan muss vollkommen sichtbar sein.
Fragen und Aufgaben:
| 1) | Belasse zunächst alle voreingestellten Werte und klicke
"Start". |
- Welchen Endwert erreicht die Stromstärke in der Spule? (Diagramm oben)
- Erkläre, warum sich dieser Endwert nicht sofort ergibt.
- Wie hätte man diesen Endwert berechnen können?
- Welchen Anfangswert und welchen Endwert hat die Selbstinduktionsspannung? (Diagramm unten)
| 2) | Ändere nun die Eigeninduktivität L im Bereich zwischen 1 und 20 mH ab und starte neu. |
- Wie ändert sich die Anstiegsgeschwindigkeiten der Stromstärke- und Spannungskurve dabei?
- Ändert sich der Endwert der Stromstärke?
- Ändert sich der Startwert der Induktionsspannung?
| 3) | Untersuche nun auch den Ausschaltvorgang. |
- Was kann man über den Verlauf der Induktionsspannung aussagen? Erkläre!
| 4) | Erhöhe nun die Größe des Außenwiderstandes
Ra auf 20 Ohm, 50 Ohm, 100 Ohm und wiederhole das Experiment. |
- Welcher Startwert der Induktionsspannung ergibt sich jeweils?
- Was ändert sich an der "Steilheit" des Abfallens der Stromstärke- und Spannungskurve?
| 5) | Verringere nun den Wert des Außenwiderstandes Ra auf 1 Ohm oder weniger. |
- Was passiert?
- Kannst du nun die Funktion des Widerstandes Rs im Schaltbild oben erklären?
| 6) | In der Simulation kann man eine Zerstörung der Bauteile
verhindern, wenn man die Darstellungsweise "ideal" aktiviert. |
- Welchen Startwert hat die Induktionsspannung beim Ausschalten, wenn Ra = 0 Ohm ist?
- Warum funktioniert diese Schaltung in der Realität nicht?
2.) Bildschirmphotos des Realexperiments.
Vergleiche deine Beobachtungen aus der Simulation mit diesen Photos eines Realexperiments mit dem Aufbau, der ganz oben auf dieser Seite im Photo gezeigt ist.
| kleine Eigeninduktivität L | große Eigeninduktivität L |
 |
 |
| Die Stromstärkekurve (oben) und die Spannungskurve (unten) steigen
schnell an und fallen schnell ab. Wird L immer kleiner, so erhält man im Grenzfall, was man ohne Induktion erwarten würde: Beim Einschalten steigen Stromstärke und Spannung sofort auf den Endwert an und fallen beim Ausschalten auch sofort wieder auf 0 ab. |
Die Stromstärke- und die Spannungskurve steigen langsam an und fallen langsam ab. |
| Außenwiderstand Ra klein | Außenwiderstand Ra groß |
 |
 |
| Hier ist der Außenwiderstand klein. Stromstärke- und Spannungskurven fallen beim Ausschalten langsam ab. Die Induktionsspannung zu Beginn des Einschaltvorgangs und zu Beginn des Ausschaltvorgang sind betragsmäßig praktisch gleich groß (untere Kurve). |
Hier ist der Außenwiderstand groß Die Stromstärkekurve fällt beim Ausschalten scheller ab, daher ist die Induktionsspannung dann auch größer. |
 |
 |
| Hier ist nur die Spannung dargestellt. Könnte man Ra + Rs wirklich auf 0 Ohm regeln, dann wären die Spannungbeträge beim Einschalt- und beim Ausschaltvorgang genau gleich groß. |
Die Spannung beim Ausschaltvorgang ist deutlich größer als beim Einschaltvorgang. |
Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang
Christian und Mario Belloni vom Davidson College, USA (Copyright Hinweise) |


