Entladen eines Kondensators und Selbstinduktion beim Ausschalten - ein Vergleich.

Diese Seite richtet sich nur an solche Schülerinnen und Schüler der Kursstufe, die im Mathematikunterricht bereits die Exponentialfunktionen kennen gelernt haben, vor allem aber an Studentinnen und Studenten der Anfangssemester.

Es wird gezeigt, dass das Entladen eines Kondensators über einen Widerstand und die Selbstinduktion in einer Spule beim Ausschalten einige Gemeinsamkeiten haben:

• in beiden Fällen gibt nur eine veränderliche Spannung,
• sie bestimmt die Stromstärke im Stromkreis
• in beiden Fällen kommt man zu einer Differentialgleichung 1. Ordnung, deren Lösungsfunktion eine Exponentialfunktion ist.

	Entladen eines Kondensators	Selbstinduktion beim Ausschalten
Was beim Einschalten passiert ist	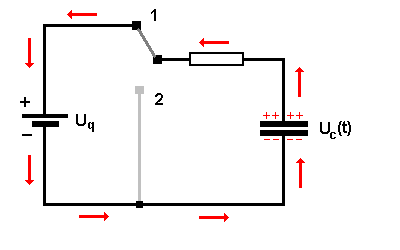Beim Ladevorgang lädt sich der Kondensator C über den Widerstand R auf. Je mehr Ladung Q(t) auf den Platten ist, desto größer wird auch die Spannung am Kondensator Uc(t). Der Ladevorgang ist beendet, wenn diese Spannung gerade so groß ist wie die Spannung der Quelle Uq.	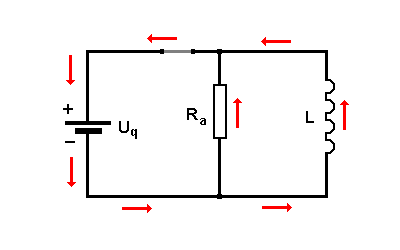Wird der Schalter geschlossen, steigt die Stromstärke in der Spule an und ein Magnetfeld wird aufgebaut. Dazu ist Energie notwendig. Nach einiger Zeit erreicht der Strom in der Spule den Endwert Iend = Uq / Rsp. Von diesem Wert aus muss beim Ausschalten die Selbstinduktion dann auch starten. Für den Einschaltvorgang spielt es keine Rolle, ob ein Parallelwiderstand Ra vorhanden ist oder nicht.
Die Quelle wird "abgehängt" - es wirkt nur noch eine Spannungsquelle	Wird der Schalter in Stellung 2 gebracht, dann wird die Quelle "abgehängt" (grau = inaktiv). Der Kondensator entlädt sich über den Widerstand R. Die Ladung Q(t) auf den Kondensatorplatten nimmt dabei ab und die Spannung Uc(t) sinkt deshalb. 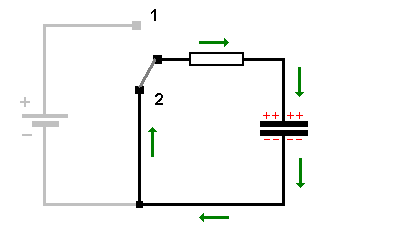Beachte, dass die Flussrichtung der Elektronen genau umgekehrt wie beim Ladevorgang ist (grüne bzw. rote Pfeile) Wir denken uns den Schalter weg und verschieben den Widerstand auf die linke Seite. Damit erhalten wir folgende vereinfachte Schaltung:	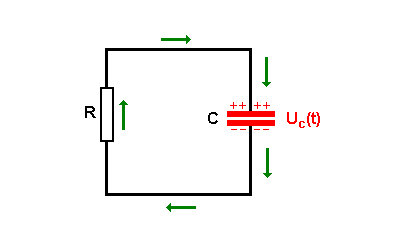Wird der Schalter geöffnet dann wird die Quelle "abgehängt" (grau = inaktiv) Eigentlich müsste dadurch der Stromfluss in der Spule sofort stoppen. Dann müsste aber die Energie des Magnetfelds der Spule sofort verschwinden. Das verletzt den Energieerhaltungssatz! Daher "wehrt" sich die Spule mit einer Selbstinduktionsspannung gegen diese Änderung der Stromstärke: Betrag und Richtung des Stromflusses bleibt im ersten Moment erhalten (Lenzsche Regel). 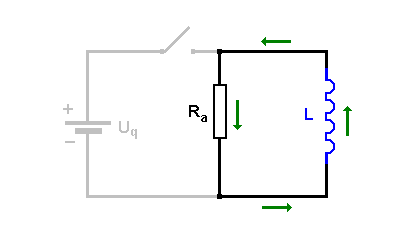Die Spule wird durch eine Reihenschaltung aus der Selbstinduktionsspannung Uind(t) und dem Spulenwiderstand Rsp ersetzt 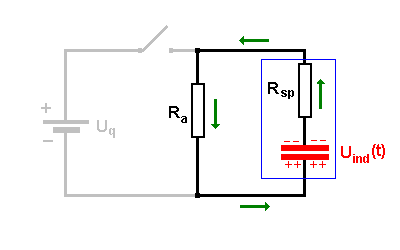Nun wird der Spulenwiderstand Rsp noch nach links verschoben. Er addiert sich mit dem äußeren Widerstand Ra zum Gesamtwiderstand Rges. Um es einfacher zu machen, schreiben wir für Rges in der folgenden Betrachtung einfach nur R.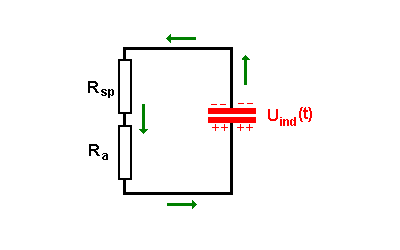
Spannungs- und Stromstärkegleichung	Es gilt für die Spannung am Kondensator Uc(t):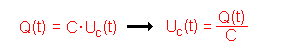 Für die Stromstärke I(t) gilt: 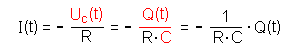das Minuszeichen berücksichtigt, dass die Richtung des Stroms beim Entladen umgekehrt ist wie beim Ladevorgang (s.o.).	Es gilt für die Induktionsspannung Uind(t):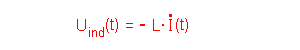 Für die Stromstärke I(t) gilt: 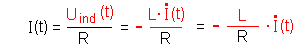das Minuszeichen berücksichtigt, dass die Induktionsspannung der Quelle entgegenwirkt.
Der Weg zur Differentialgleichung	Nun gilt aber für die Momentanstromstärke I(t):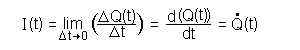 Damit ergibt sich eine Differentialgleichung 1. Ordnung (DGL):	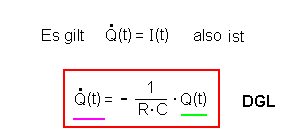Damit ergibt sich eine Differentialgleichung 1. Ordnung (DGL):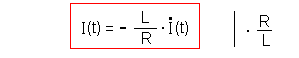 wenn man möchte, kann man das noch umformen: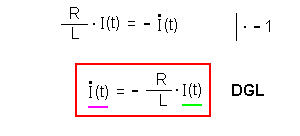
Lösungsansatz		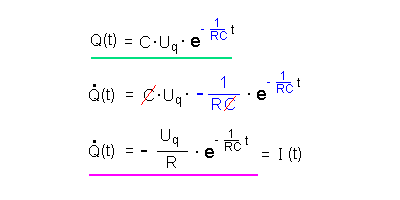Wie ganz oben schon ausgeführt, muss die Stromstärke beim Ausschaltvorgang mit dem Wert starten, den sie am Ende des Einschaltvorgangs erreicht hat, also mit I(t = 0s) = Uq / Rsp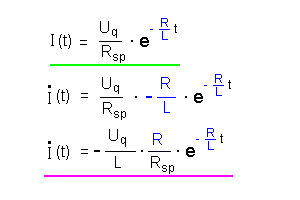 ( Erinnerung R steht für Rges deshalb kann man die Widerstände R und Rsp nicht einfach kürzen)
Lösungsprobe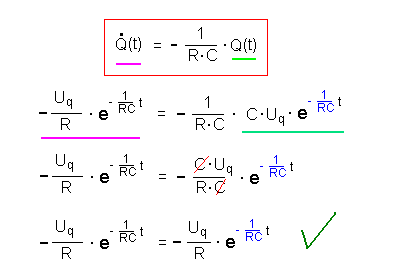
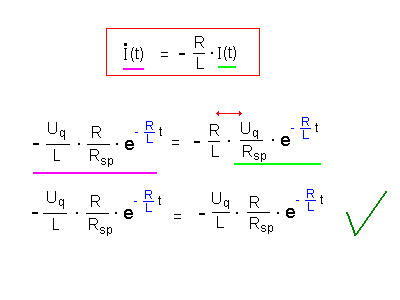Lösungsgleichungen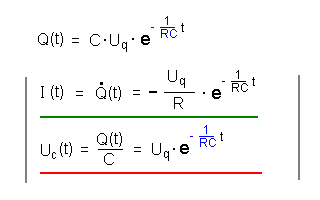
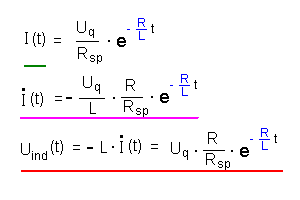Beginn des Vorgangs (A)	Für t = 0 s wird der Exponentialausdruck 1 (blaue Einsetzung). Für den Beginn des Vorgangs ergibt sich also:	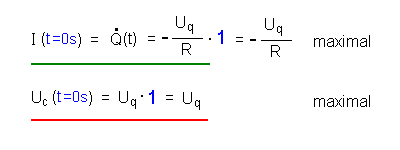Für t = 0 s wird der Exponentialausdruck 1 (blaue Einsetzung). Für den Beginn des Vorgangs ergibt sich also: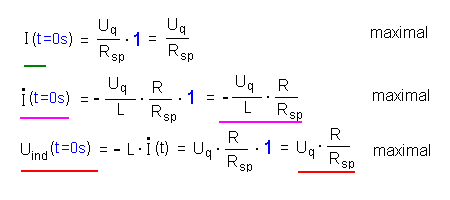
Ende des Vorgangs (B)	Für t → ∞ wird der Exponentialausdruck 0 (blaue Einsetzung). Für das Ende des Vorgangs ergibt sich also:	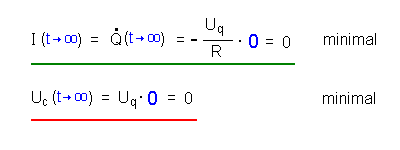Für t → ∞ wird der Exponentialausdruck 0 (blaue Einsetzung). Für das Ende des Vorgangs ergibt sich also: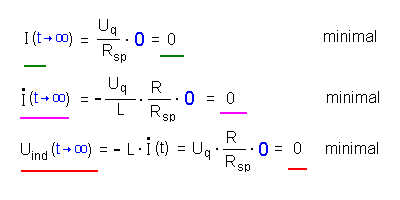
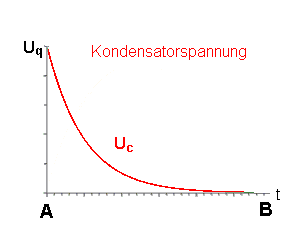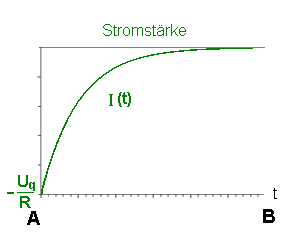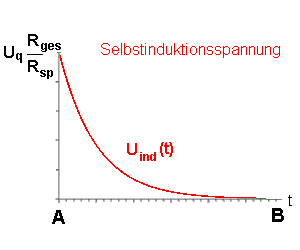Schaubilder Spannungen und Stromstärke		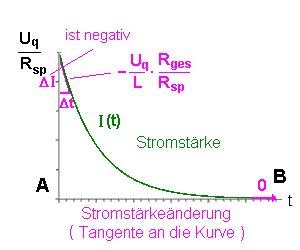Der Faktor Rges / Rsp bestimmt, wie die Kurve genau verläuft: Ist der Außenwiderstand Ra groß, dann ist es Rges auch, da Rges=Rsp + Ra ist. In diesem Fall startet der Vorgang mit einer Selbstinduktionsspannung, die auch deutlich größer als Uq sein kann. Die Stromstärke nimmt dann allerdings auch sehr schnell ab.
Links zur ausführlichen Behandlung des Problems	Entaden eines Kondensators über einen Widerstand (mit Exponentialfunktion)	Selbstinduktion beim Ausschalten (mit Exponentialfunktion) Selbstinduktion beim Ausschalten