Laden eines Kondensators und Selbstinduktion beim Einschalten - ein Vergleich.

Diese Seite richtet sich nur an solche Schülerinnen und Schüler der Kursstufe, die im Mathematikunterricht bereits die Exponentialfunktionen kennen gelernt haben, vor allem aber an Studentinnen und Studenten der Anfangssemester.

Es wird gezeigt, dass das Laden eines Kondensators über einen Widerstand und die Selbstinduktion in einer Spule einige Gemeinsamkeiten haben:

• in beiden Fällen gibt es die konstante Spannung der Quelle und eine veränderliche Spannung,
• diese veränderliche Spannung wirkt dabei der Spannung der Quelle entgegen,
• beide Spannungen ergeben zusammen die Gesamtspannung. Sie bestimmt die Stromstärke im Stromkreis
• in beiden Fällen kommt man zu einer Differentialgleichung 1. Ordnung, deren Lösungsfunktion eine Exponentialfunktion ist.

	Laden eines Kondensators	Selbstinduktion beim Einschalten
Das Schaltbild	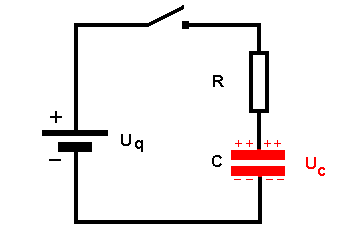Wird der Schalter geschlossen, so lädt sich der Kondensator C über den Widerstand R auf. Je mehr Ladung Q auf den Kondensatorplatten ist, um so größer wird auch die Spannung UC.	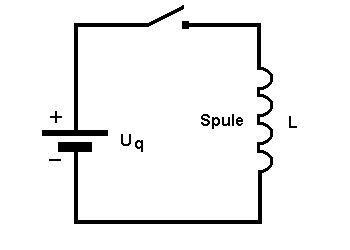Wird der Schalter geschlossen, so wird die Spule von einem Strom durchflossen und es entsteht eine Selbstinduktionsspannung. Die Größe der Selbstinduktionsspannung hängt von der Änderung des Stroms in der Spule ab.
Die Spannungen werden zur Gesamtspannung zusammengefasst.	Das Schaltbild von oben wird einfach übernommen. Die Quelle und der Kondensator werden in die untere Leitung verschoben. 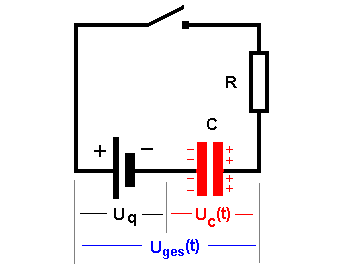Die veränderliche Spannung am Kondensator Uc(t) (rot) wirkt der konstanten Spannung der Quelle Uq(schwarz) entgegen. Beide Spannungen zusammen bestimmen die veränderliche Gesamtspannung Uges(t) (blau)	Die reale Spule wird in den Spulenwiderstand R und die veränderliche Selbstinduktionsspannung Uind(t) zerlegt.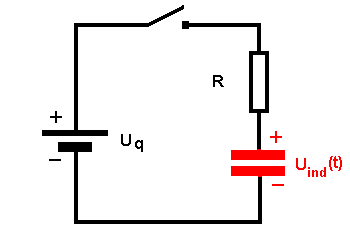 Quelle und Selbstinduktionsspannung werden in die untere Leitung verschoben. 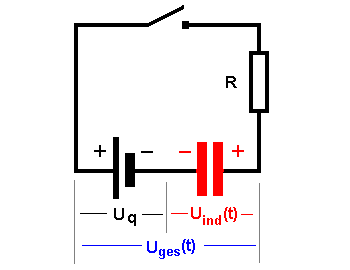Die veränderliche Induktionsspannung Uind(t) (rot) wirkt der konstanten Spannung der Quelle Uq (schwarz) entgegen. Beide Spannungen zusammen bestimmen die veränderliche Gesamtspannung Uges(t) (blau)
Spannungs- und Stromstärkegleichung	Es gilt für die Spannung am Kondensator UC(t):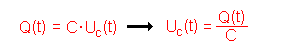 Die Gesamtspannung Uges (t) ist die Summe der Einzelspannungen. Wir müssen aber noch mit einem Minuszeichen berücksichtigen, dass die Spannung am Kondensator Uc (t) der Spannung der Quelle entgegenwirkt: 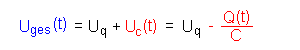Für die Stromstärke I(t) gilt:	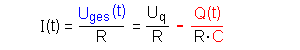Es gilt für die Induktionsspannung Uind(t):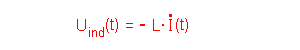 Die Gesamtspannung Uges (t) ist die Summe der Einzelspannungen. Im Ausdruck für die Selbstinduktionsspannung Uind (t) berücksichtigt das Minuszeichen bereits, dass Uind (t) der Spannung der Quelle entgegenwirkt (Lenzsche Regel): Für die Stromstärke I(t) gilt: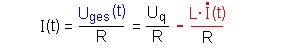
Der Weg zur Differentialgleichung	Nun gilt aber für die Momentanstromstärke I(t):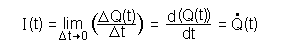 Damit ergibt sich eine Differentialgleichung 1. Ordnung (DGL):	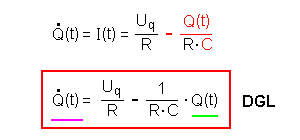Damit ergibt sich eine Differentialgleichung 1. Ordnung (DGL):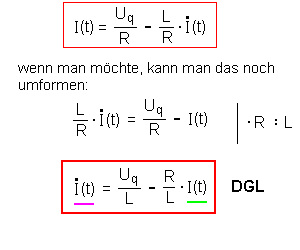
Lösungsansatz	Für die Lösung der Differentialgleichung machen wir folgenden Ansatz: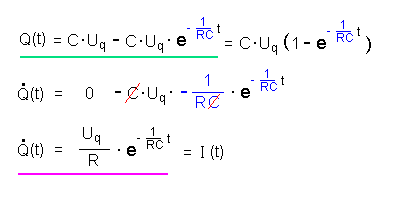 Warum gerade dieser Ansatz sinnvoll ist, wird später klar, wenn wir überlegen, was für sich für t = 0 s und für t → ∞ ergibt (s.u.). Zunächst wollen wir prüfen, ob der Ansatz die DGL überhaupt löst.	Für die Lösung der Differentialgleichung machen wir folgenden Ansatz: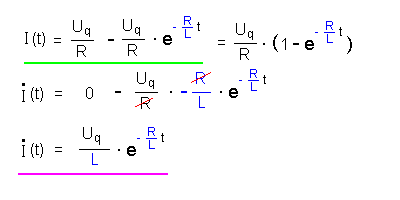 Warum gerade dieser Ansatz sinnvoll ist, wird später klar, wenn wir überlegen, was für sich für t = 0 s und für t → ∞ ergibt (s.u.). Zunächst wollen wir prüfen, ob der Ansatz die DGL überhaupt löst.
Lösungsprobe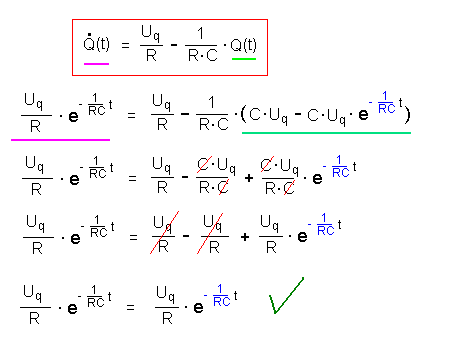
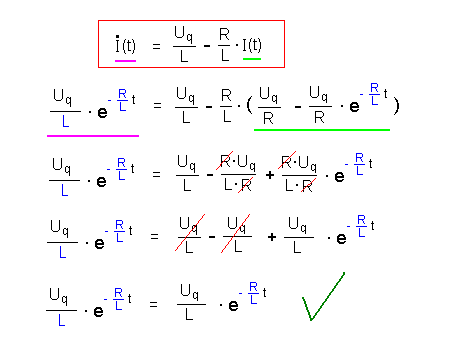Lösungsgleichungen	Damit finden wir folgende Lösungsgleichungen: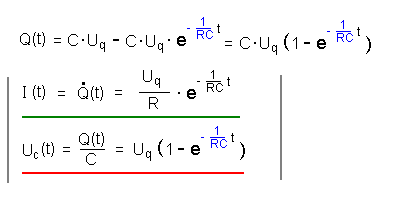	Damit finden wir folgende Lösungsgleichungen: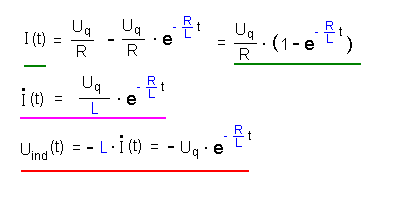
Beginn des Vorgangs (A)	Für t = 0 s wird der Exponentialausdruck 1 (blaue Einsetzung). Für den Beginn des Vorgangs ergibt sich also:	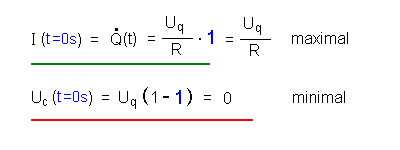Für t = 0 s wird der Exponentialausdruck 1 (blaue Einsetzung). Für den Beginn des Vorgangs ergibt sich also: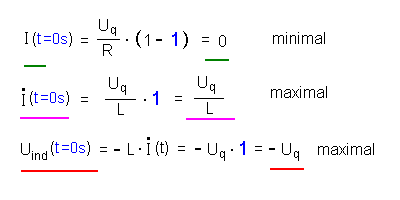
Ende des Vorgangs (B)	Für t → ∞ wird der Exponentialausdruck 0 (blaue Einsetzung). Für das Ende des Vorgangs ergibt sich also:	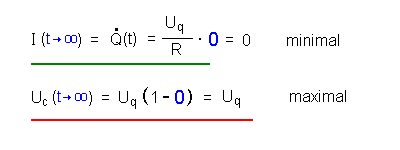Für t → ∞ wird der Exponentialausdruck 0 (blaue Einsetzung). Für das Ende des Vorgangs ergibt sich also: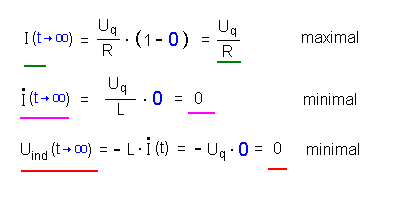
Schaubilder Spannungen und Stromstärke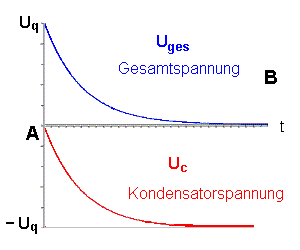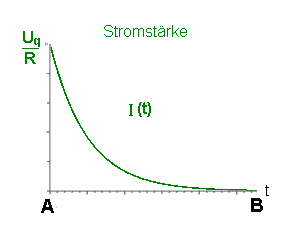
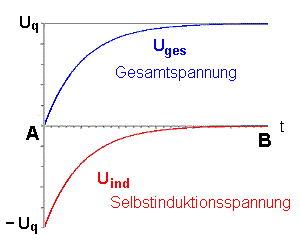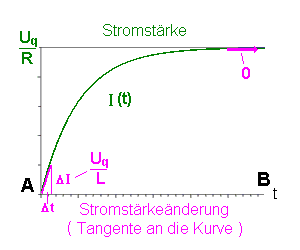Ausführliche Behandlung des Problems	Laden eines Kondensators über einen Widerstand (mit Exponentialfunktion)	Selbstinduktion beim Einschalten (mit Exponentialfunktion)

Gemeinsamkeiten und Unterschiede:

1.) Gemeinsamkeiten:

In beiden Fällen

• wirken im Stromkreis zwei Spannungsquellen - die konstante Spannung der Quelle und eine veränderliche Spannung.
  
  
• wirkt die veränderliche Spannung der Spannung der Quelle entgegen.
  
  
• bestimmt die Gesamtspannung zusammen mit einem Widerstand R die Stromstärke im Stromkreis.
  
  
• ergibt sich eine Differentialgleichung 1. Ordnung, deren Lösung eine Exponentialfunktion ist.

2.) Unterschiede:

Zu Beginn des Vorgangs (direkt beim Schließen des Schalters)

• ist der Kondensator ungeladen, damit ist die Spannung U_c (t = 0 s) = 0.
  Die Gesamtspannung ist dann also maximal und der Ladestrom auch.
  
  
• beginnt die Spule erst ein Magnetfeld aufzubauen, der Strom in ihr steigt von 0 A aus an.
  Der Strom ist also zu Beginn minimal, die Gesamtspannung auch.
  Die Selbstinduktionsspannung schafft es ganz zu Beginn, die Spannung der Quelle komplett zu kompensieren (U_ind(t = 0 s) = - U_q).

Nach unendlich langer Zeit

• ist der Kondensator voll geladen, damit ist die Spannung U_c (t → ∞) = - U_q. Die Gesamtspannung wird 0 V(minimal) ebenso der Ladestrom.
  
  
• hat die Spule ihr Magnetfeld komplett aufgebaut. Die Stromstärke wächst nicht mehr weiter an, sie wird maximal - sie erreicht ihren Endwert. Dies ist der Wert, den man ohne Selbstinduktion sofort erwartet hätte (U_q / R ).
  Die Selbstinduktionsspannung wird nun 0. Die Gesamtspannung ist nun die Spannung der Quelle.

Beide Vorgänge erfolgen gewissermaßen gegenläufig. Dies zeigen auch die entsprechenden Diagramme.

Grüninger, Landesbildungsserver, 2016