Elektronen im homogenen Magnetfeld

Für die Wiedergabe benötigt man die Java-Runtime-Environment.
Wenn Sie diese nicht haben, können Sie sie  hier kostenlos herunterladen.
In den Einstellungen des Browsers muss Javascript aktiviert sein.

Im Java-Applet sieht man einen Bereich (hellblau) in dem ein Magnetfeld wirkt. Die Richtung des Magnetfeldes ist durch die Richtung der dunkelblauen Pfeile angegeben. (vgl. auch rechts) In der Mitte der Anordnung befindet sich ein (dunkelgrauer) Strahlerzeuger, der rot gezeichnete Elektronen ausschickt. Die Geschwindigkeit der Elektronen und die Stärke und Orientierung des Magnetfeldes kann durch Auswahlfelder beeinflusst werden. Mit Kontrollkästchen kann man auswählen, welche Größen eingezeichnet werden sollen.

Arbeite die Fragen und Aufgaben Punkt für Punkt durch.
Sie führen Dich Schritt für Schritt durch das Thema. Halte Dich dabei an die Anweisungen.

Fragen und Aufgaben:

1.) Bahnkurve

Belasse zunächst die Grundeinstellungen und klicke auf "Start".

• Welche Bahn durchläuft das (rote) Elektron?

Ändere im Auswahlfeld "Magnetfeldrichtung" die Richtung des Feldes auf "aus der Zeichenebene heraus". Klicke wieder "Start".

• Wie verläuft die Bahn des Elektrons nun? Woran liegt das?

;Nach oben zum Applet

2.) Die Lorentzkraft bestimmt die Bahnkurve

Erinnerung: Bewegte Ladungen (also auch Elektronen) erfahren in einem Magnetfeld eine Kraft - die Lorentzkraft. Die Richtung der Lorentzkraft kann man mit der Drei-Finger-Regel der linken Hand (negative Ladungen) finden: zeigt der Daumen in Bewegungsrichtung des Teilchens (grün), und der Zeigefinger in die Richtung des Magnetfeldes (blau), so gibt der Mittelfinger die Richtung der Lorentzkraft (violett) an.

Starte diesmal die Animation nicht, sondern arbeite nur mit den Kontrollkästchen.
Klicke das Kontrollkästchen bei "Geschwindigkeit" an und setzte dort ein Häkchen.
(Der Vektor der Bahngeschwindigkeit wird nun angezeigt.)

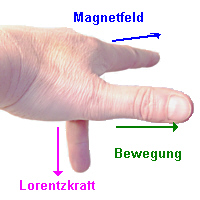
• Bestimme mit Hilfe der Drei-Finger-Regel der linken Hand die Richtung der Lorentzkraft.
• Klicke danach das Kontrollkästchen bei "Lorentzkraft" an und überprüfe Dein Ergebnis!

Ändere die Magnetfeldrichtung auf "aus Zeichenebene heraus".

• In welche Richtung deutet die Lorentzkraft nun?

Ändere die Magnetfeldrichtung auf "parallel zur Geschwindigkeit" und "antiparallel zur Geschwindigkeit".

• Warum tritt beide Male keine Lorentzkraft auf?
• In welche Richtung würde die Lorentzkraft deuten, wenn der Vektor des Magnetfeldes zum unteren Bildschirmrand hin weist?

;Nach oben zum Applet

3.) Die Lorentzkraft weist den Weg zum Mittelpunkt der Kreisbahn.

Nun sind die Kontrollkästchen bei "Geschwindigkeit" und bei "Lorentzkraft" gesetzt, so dass beide Vektoren angezeigt werden.
Stelle bei "Magnetfeldrichtung" wieder "in die Zeichenebene hinein" ein.

• Lasse nun auch noch die "Mittelpunktslinie" anzeigen. Sie verläuft vom Eintrittspunkt des Elektrons in das Feld aus in die Richtung, in welche die Lorentzkraft deutet.

Irgendwo auf dieser Linie muss der Mittelpunkt M der Kreisbahn liegen, aber wo?

;Nach oben zum Applet

4.) Der Radius der Kreisbahn hängt von der Geschwindigkeit v und der Stärke des Magnetfelds B ab.

Klicke nun auch noch das Kontrollkästchen bei "Radius" an. Der Mittelpunkt der Kreisbahn wird angezeigt.
Starte nun wieder die Animation durch Klicken von "Start".

• Wie verändert sich also der Bahnradius r, wenn man die Geschwindigkeit des Elektrons verkleinert?
  (Wähle bei "Geschwindigkeit" nun 1 * 10⁷ m/s aus und probiere es aus).
  
  
• Wie verändert sich der Bahnradius r, wenn das Magnetfeld B stärker ist?
  (Wähle bei "Stärke des Feldes B" nun 2 mT statt 1 mT aus)
  
  
• Mit welcher Kombination von Geschwindigkeit v und Stärke des Feldes B wird der Bahnradius besonders klein / besonders groß?

;Nach oben zum Applet

5.) Die Umlaufzeit T verhält sich seltsam....

In der Animation wird oben die aktuelle Zeit eingeblendet.
Stelle als Stärke des Feldes nun 1 mT ein. Wähle verschiedene Geschwindigkeiten v aus und beobachte jedes Mal, wie lange das Elektron für einen Umlauf benötigt.

• Was fällt dabei auf?
• Kannst Du das anschaulich erklären?
• Kannst Du es auch mathematisch beweisen? ( Tipp: T = 2*π*r / v)

Durch die Bahngeschwindigkeit v lässt sich also die Umlaufzeit T nicht beeinflussen. Elektronen verschiedener Geschwindigkeit benötigen alle gleich lang für einen Kreisumlauf!

• Wie kann man dann die Umlaufdauer T eines Elektrons beeinflussen?

;Nach oben zum Applet

Arbeitsblatt zu dieser Seite: AB_Elektronen_im_B-Feld.doc (36,5 kB)

Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:

Sie müssen dazu die gepackte Datei (e_bfeld.zip) herunterladen und in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder. Die nötigen Java-Achive sind ebenfalls enthalten.

Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.

Nutzungsbedingungen:

Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und Kollegen weitergeben.

Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der ausdrücklichen Zustimmung.

Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang Christian und Mario Belloni vom Davidson College, USA ( Copyright Hinweise) © Javascript dieses Problems: Klaus-Dieter Grüninger, Landesbildungsserver Baden-Württemberg, 2008