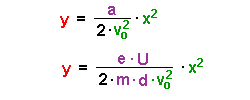Elektronen im elektrischen Querfeld.

Das nebenstehende Foto zeigt ein Realexperiment zur Simulation auf dieser Seite. Man erkennt ganz rechts ein Strahlerzeugungssystem, das einen Elektronenstrahl erzeugt. Anschließend treten die Elektronen auf der Mittelachse senkrecht in das elektrische Feld eines Plattenkondensators ein. Man erkennt oben und unten die Kondensatorplatten, die untere Platte ist positiv geladen. Ein Teil der Elektronen trifft auch den (blau) fluoreszierenden Schirm, so dass man die Bahn der Elektronen verfolgen kann. An was erinnert die Bahnkurve der Elektronen?

In der Simulation ist die Orientierung umgekehrt: das "Strahlerzeugungssystem" befindet sich links.

Fragen / Aufgaben:

1.) Erste Orientierung in der Simulation.

Wenn man in der Simulation die linke Maustaste drückt, dann bekommt man die Koordinaten der Maus (in m) angezeigt. Man kann so Entfernungen messen.

• Wie groß ist der Plattenabstand d?
• Wie lange sind die Kondensatorplatten?

nach oben zum Applet

2.) Die Spannung an den Platten wird abgeschaltet.

Wähle zunächst die Spannung an den Platten mit 0 V (keine Spannung angelegt).

• Wie lange benötigt das Elektron durch den Kondensator?
• Wie lange benötigt es bis zur Kondensatormitte?
• Wie lange benötigt es für 1 cm?
• Was für eine Art Bewegung führt es also in horizontaler Richtung aus?

nach oben zum Applet

3.) Spannung an den Kondensatorplatten.

Lege nun eine Spannung an die Platten an, indem du den Schieberegler für die Spannung nach rechts verschiebst.

• Was passiert bei einer sehr kleinen angelegten Spannung (z.B. 10 V)?
• Was passiert bei einer großen angelegten Spannung (z.B. 100 V)?
• Versuche zu erklären, warum sich die Kurven so unterscheiden.
• Ab welcher Spannung schafft es das Elektron gerade noch / gerade nicht mehr durch den Kondensator?

nach oben zum Applet

4.) Die Spannung wird umgepolt.

Pole die Quelle um (Auswahlfeld Polung oben rechts).

• Was ist nun anders als vorher?
• Was hat sich nicht verändert?

nach oben zum Applet

5.) Der Betrag der Vertikalgeschwindigkeit.

Stelle als Spannung an den Kondensatorplatten 114 V ein.

• Welche Vertikalgeschwindigkeit v_y hat das Elektron nach 2,0 s?
• Wie weit ist es dann in x-Richtung vorangekommen?
• Welche Geschwindigkeit v_y hat es nach der doppelten Zeit (4,0s)?
• Bei welcher x-Koordinate ist es zu diesem Zeitpunkt?
• Welchen Zusammenhang zwischen v_y und x bzw. zwischen v_y und t lässt dies vermuten?

nach oben zum Applet

Die Theorie hinter der Simulation.

Sicher bist du zum Ergebnis gekommen, dass sich ohne angelegte Spannung das Elektron in horizontaler Richtung gleichförmig bewegt.
Legt man eine Spannung an, so wirkt in y-Richtung eine konstante Kraft entweder nach oben oder nach unten.
Diese Kraft ergibt eine konstante Beschleunigung, die auf das Elektron in y-Richtung wirkt.

Die beide Bewegungen überlagern sich und führen zu der bekannten Parabelbahn.

Du hast sicher erkannt, dass die Bewegung also im Prinzip genauso verläuft wie  beim waagrechten Wurf in der Mechanik.

Diese Parallele wollen wir hier noch etwas genauer gegenüberstellen:

Mechanik : waagrechter Wurf	Elektrizitätslehre: geladenes Teilchen im Kondensator
horizontale Richtung: gleichförmige Bewegung	horizontale Richtung: gleichförmige Bewegung
vertikale Richtung: es wirkt eine konstante Kraft, die Gewichtskraft Fg. Diese führt zu einer konstanten Beschleunigung g	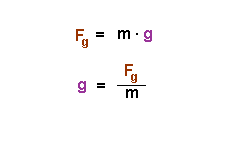vertikale Richtung: es wirkt eine konstante Kraft, die elektrische Kraft Fel. Diese führt zu einer konstanten Beschleunigung a: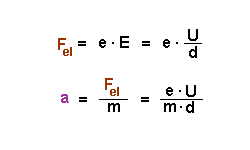
Für die in y-Richtung zurückgelegte Wegstrecke s gilt: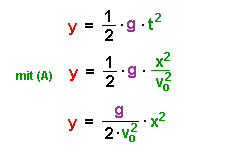 Dies ist die Gleichung einer Parabel.	Für die in y-Richtung zurückgelegte Wegstrecke s gilt: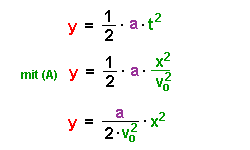 Dies ist die Gleichung einer Parabel. Wenn man a einsetzt, ergibt sich:
Für die Geschwindigkeitskomponente in y-Richtung gilt: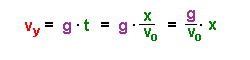 Die y-Komponente der Geschwindigkeit vywächst also linear mit der Zeit t, bzw. linear zur Ortskomponente x.	Für die Geschwindigkeitskomponente in y-Richtung gilt: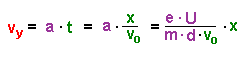 Die y-Komponente der Geschwindigkeit vy wächst also linear mit der Zeit t, bzw. linear zur Ortskomponente x.

Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:

Sie müssen dazu die gepackte Datei (e_efeld_q.zip) herunterladen und in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder. Die nötigen Java-Achive sind ebenfalls enthalten.

Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.

Nutzungsbedingungen:

Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und Kollegen weitergeben.

Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der ausdrücklichen Zustimmung.

Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang Christian und Mario Belloni vom Davidson College, USA   (Copyright Hinweise) © Javascript dieses Problems: Klaus-Dieter Grüninger, Landesbildungsserver Baden-Württemberg