Elektronen im elektrischen Längsfeld - verzögerte Bewegung.

Ein Elektron (blauer Punkt) kommt mit gegebener Anfangsgeschwindigkeit (Auswahlfeld) durch eine Lücke in der linken Platte.
An die Kondensatorplatten (Plattenabstand d = 0,04 m) ist eine Spannung U_C angelegt.
Dadurch wird eine Feldkraft F_el entgegen der Bewegungsrichtung erzeugt, die das Elektron bremst.

Kann es die rechte Platte erreichen, und wovon hängt dies ab?

Aufgaben / Fragen :

a) Belasse zunächst die Grundeinstellungen und klicke "Start".

• Warum kehrt das Elektron um?
• Wann kehrt das Elektron um?
• Wie weit von der linken Platte liegt der Umkehrpunkt entfernt?
• Mit welcher Geschwindigkeit erreicht es wieder die linke Platte (v-t-Diagramm)?

nach oben zum Applet

b) Halbiere nun die Spannung (140 V).

• Wie weit kommt das Elektron nun?
• Welchen Zusammenhang zwischen dem Umkehrpunkt und der Spannung lässt dies vermuten?

nach oben zum Applet

c) Verändere nun die Spannung am Kondensator weiter.

• Bei welcher Spannung schafft es das Elektron gerade durch den Kondensator?
• Vergleiche mit der ursprünglichen Spannung aus a)!

nach oben zum Applet

d) Verdopple die Geschwindigkeit (Auswahlfeld oberhalb des Applet)

• Bei welcher Spannung liegt nun die Grenze zwischen "Durchkommen" und "nicht Durchkommen"?
• Vergleiche mit den Ergebnissen aus c)!
• Arbeite die Theorie hinter der Simulation unten auf dieser Seite durch.

nach oben zum Applet

Die Theorie hinter der Simulation.

Verschiedene Experimente folgen demselben physikalischen Prinzip:

Vielleicht hast du bemerkt, dass folgende unterschiedliche Bewegungen nach demselben physikalischen Prinzip ablaufen:

•  die verzögerte Bewegung eines Elektrons im Kondensator
•  das (gleichmäßige) Bremsbewegung eines Fahrzeugs (ohne Reaktionszeit)
• der senkrechte Wurf eines Körpers (ohne Luftreibung).

Diese Parallele soll hier noch etwas genauer verglichen werden:
In der Darstellung wird der Kondensator um 90 Grad gedreht um den Vergleich deutlicher zu machen.

Außerdem wird eine positive Ladung betrachtet um die Parallele im Feldverlauf deutlicher werden zu lassen.

senkrechter Wurf	Verzögerte Elektronenbewegung
Die Bewegung erfolgt von unten nach oben: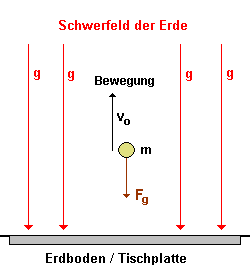	Die Bewegung erfolgt von unten nach oben: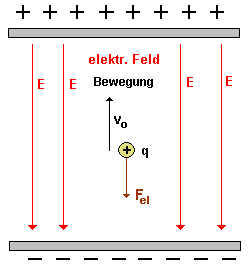
- konstantes Schwerefeld - konstante, verzögernde Kraft Fg entgegen der Bewegungsrichtung des Körpers bremst den Körper ab.	- konstantes E-Feld - konstante, verzögernde Kraft Fel entgegen der Bewegungsrichtung der Ladung bremst die Ladung ab.
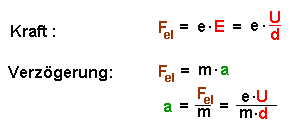Könnte man die Gravitation "abschalten", dann würde sich die Kugel mit konstanter Geschwindigkeit v0 gleichförmig nach oben bewegen.	Wenn man das Feld abschaltet (keine Spannung am Kondensator angelegt), dann bewegt sich die Ladung mit konstanter Geschwindigkeit v0 gleichförmig nach oben.
Dann würde gelten: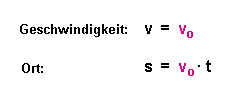	Dann gilt: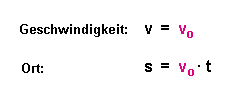
Mit Gravitation wird die Geschwindigkeit und der zurückgelegte Weg aber kleiner (Superpositionsprinzip):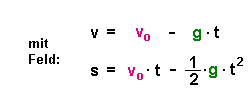	Mit elektrischem Feld wird die Geschwindigkeit und der zurückgelegte Weg aber kleiner (Superpositionsprinzip):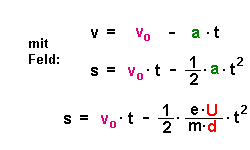
Im Augenblick des Umkehrens kommt der Körper kurz zur Ruhe, also gilt: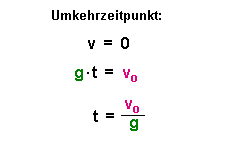	Im Augenblick des Umkehrens kommt die Ladung kurz zur Ruhe, also gilt: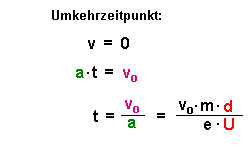
Für den Umkehrpunkt s gilt: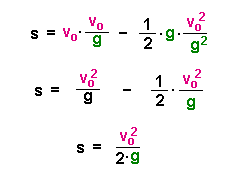	Für den Umkehrpunkt s gilt: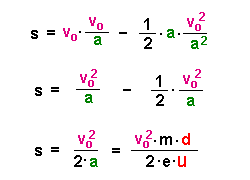
	Ist s > Plattenabstand d, dann kommt die Ladung durch den Kondensator. Ist s <  d, dann kehrt die Ladung um!

Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:

Sie müssen dazu die gepackte Datei (e_efeld_v.zip) herunterladen und in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder. Die nötigen Java-Achive sind ebenfalls enthalten.

Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.

Die Datei herunterladen : e_efeld_v.zip

Nutzungsbedingungen:

Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und Kollegen weitergeben.

Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der ausdrücklichen Zustimmung.

Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang Christian und Mario Belloni vom Davidson College, USA   (Copyright Hinweise) © Javascript dieses Problems: Klaus-Dieter Grüninger, Landesbildungsserver Baden-Württemberg