Das Potential beim Plattenkondensator und die Flammensonde.

Zwischen den Platten eines Plattenkondensators herrscht ein homogenes Feld, d.h. die el. Feldstärke E hat überall dieselbe Richtung und denselben Betrag.
Auf eine elektrische Ladung q (hier ein Elektron mit der Elementarladung e) wirkt daher eine konstante elektrische Kraft F_el = q * E (bzw. F_el = e * E).
Die Ladung führt also - je nach Ladungsvorzeichen und Feldrichtung - eine gleichmäßig beschleunigte Bewegung oder eine Bewegung mit konstanter Verzögerung aus.

Mehr dazu findet man auf der Seite Ladung, E-Feld, el. Kraft und Bewegung einer Ladung im Längsfeld eines Kondensators.

Wir betrachten hier ein Elektron, das von der linken Platte eines Plattenkondensators zur rechten Platte beschleunigt wird.

• Welche kinetische Energie hat es, wenn es auf der rechten Platte aufprallt?
• Welche Energie hat es genau in der Kondensatormitte, also nach halber Strecke?
• Welche Energie hat es an einem beliebigen Punkt im Kondensator?

Zur Hinführung auf die Thematik dient auch diese Aufgabe zur Bewegung einer Ladung im Längsfeld

1) Bewegung von der linken bis zur rechten Platte.

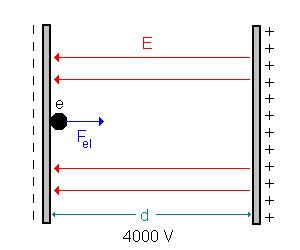Die el. Feldkraft beschleunigt das Elektron zur rechten Platte hin. Es gilt dabei: 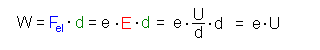Die Energie ist also das Produkt der (Elementar)ladung und der am Kondensator angelegten Spannung.

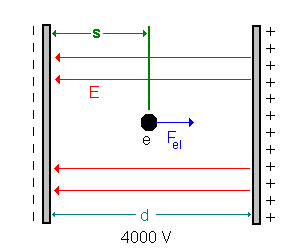
2) Energie des Elektrons genau in der Kondensatormitte.

An der elektrischen Feldstärke hat sich nichts verändert, daher ist auch die beschleunigende el. Kraft gleich geblieben. Es wurde bisher aber nur auf der halben Strecke s beschleunigt, also gilt: 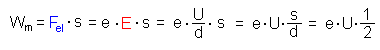Die kinetische Energie der Ladung in der Kondensatormitte ist nur halb so groß wie in 1).

3) Eine äquivalente Betrachtung.

Die rechte Platte soll nun in die Mitte verschoben werden.
Muss man dabei noch etwas ändern, damit das Elektron dann, wenn es dort auf die Platte trifft, die gleiche Energie hat wie in 2)?

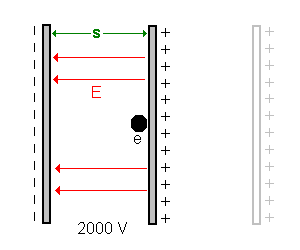Wird der Plattenabstand von d auf s halbiert, so bedeutet dies wegen E = U / Plattenabstand, dass sich dabei die elektrische Feldstärke E verdoppelt. Auf das Elektron wirkt dann eine doppelt so große Kraft Fel aber nur auf halber Strecke s, es hätte die kin. Energie wie in 1) wenn es auf die Platte auftrifft. Wir wollen aber, dass es die gleiche kinetische Energie haben soll wie in 2). Wir dürfen daher die el. Feldstärke nicht ändern! Wird der Plattenabstand halbiert, so müssen wir auch die Spannung halbieren, damit E konstant bleibt!

4) Eine abstrakte Idee bewährt sich auch im Experiment.

Im Abschnitt 3) hatten wir gedanklich die Platte zur Mitte hin verschoben und mussten dabei auch die Spannung halbieren um Feldstärke E und el. Kraft F_el unverändert zu lassen. Nun soll die rechte Kondensatorplatte wieder an ihrem alten Platz sein und die Spannung wieder 4000V betragen.

Kann man vielleicht zwischen der linken Kondensatorplatte und der Kondensatormitte eine Spannungsdifferenz von 2000V nachweisen, wenn man eine geeignete Sonde dorthin bringt?

Man muss dafür sorgen, dass zwischen den Kondensatorplatten Ladungsträger vorhanden sind. Diese erzeugt man mit Hilfe einer Flamme, sie ionisiert die Moleküle der Luft. Man bekommt so eine Flammensonde.

Zum Experiment-Video:

Zwei quadratische Platten sind in 20 cm Entfernung parallel zueinander angeordnet. An Ihnen liegt eine Spannung von 4 kV an. Die Flammensonde steht zunächst in 5 cm Entfernung von der linken Platte. Sie wird dann im Experiment zunächst in die Kondensatormitte (10 cm Entfernung von der linken Platte) und dann in 15 cm Entfernung von der linken Platte gebracht.
Beachte die Anzeige des (statischen) Voltmeters links.

Sieh' dir das Experiment-Video an.

Offenbar kann man zwischen der linken Kondensatorplatte (hier als Bezugspunkt gewählt) und jedem Punkt im Plattenkondensator eine Spannungsdifferenz nachweisen und dem Punkt ein Potential φ, zuordnen.
(Statt "Potential" ist auch die Schreibweise "Potenzial" üblich).

In der Kondensatormitte beträgt dieses Potential also 2000V, wie wir uns das schon überlegt hatten, es wächst von links nach rechts linear mit der Entfernung s an.
Der Bezugspunkt des Potentials kann im Prinzip frei gewählt werden, meist ist es aber den Minuspol der Quelle.

5) Zusammenfassung

In den Abschnitten 2) und 3) mussten wir die elektrische Feldstärke E, das Verhältnis von Potential und Plattenabstand unverändert lassen.
Es gilt also:

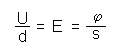
oder

Grüninger, Landesbildungsserver, 2011