Wie schnell sind Elektronen in Drähten?

1) Wagst Du einen Tipp?

Was denkst Du, wie schnell bewegen sich Elektronen in normalen (Kupfer-) Leitungsdrähten? In einem Elektronenstrahl kann ihre Geschwindigkeit schon die Größenordnung der Lichtgeschwindigkeit erreichen. Dort sind sie aber im Vakuum unterwegs. In Drähten werden sie ja ständig durch den Zusammenprall mit den Atomrümpfen gebremst. Gib - für Dich selbst - einfach einmal einen "Tipp" ab, bevor Du die Seite durcharbeitest!

2) Irgendwo muss man anfangen...

Ein Draht wird von einem Strom der Stärke I durchflossen. Dieser Strom stammt von N Elektronen, die alle die Elementarladung e tragen. Sie bewegen sich mit v = s / t durch den Draht. Löst man nach t = s / v auf, dann kommt man zu folgender Beziehung:
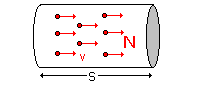Wir lösen nach v auf:

Für eine Zahlenrechnung ergeben sich einige Probleme:

• Welche Leiterlänge s sollen wir annehmen?
• Welche Stromstärke I sollen wir einsetzen?
• Wie groß ist die Zahl der Elektronen N im Leiterstück?
  (Hängt sicher auch von der Länge s ab)

Wir ersetzen N - die Zahl der Elektronen im Drahtstück - durch die Elektronendichte n.
Es sieht zunächst so aus, als ob das die Sache nur komplizierter macht, wir haben so aber ein Problem weniger, wie wir gleich sehen werden:

also folgt für N:

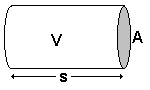Wir setzen (2) in (1) ein:

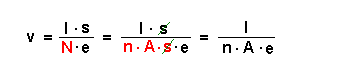
In dieser Form kommt es nicht mehr auf die Länge des Leiterstücks an.

Zur besseren Anschauung können wir uns folgendes Modell denken, das wir aus dem Alltag kennen.
Der Leiter entspricht einer Straße und die Elektronen den Autos.

Der "Durchsatz" einer Straße ist die Zahl der Fahrzeuge, die z.B. je Minute die Straße passieren können, dies entspricht der Verkehrsstromstärke und damit der elektrischen Stromstärke I.
(Dabei erfolgt Straßenverkehr - leider! - immer zweidimensional, wir können einen Stau nicht überfliegen).

• Wenn mehr Fahrzeuge pro Minute eine bestimmte Stelle passieren sollen (I), dann müssen die Fahrzeuge schneller fahren (v).
  
• Hat man zwei Fahrspuren (entspricht A), dann kommen bei gleicher Geschwindigkeit auch doppelt so viele Fahrzeuge pro Zeiteinheit an der Stelle vorbei.
  
• Die Fahrzeugdichte (Fahrzeuge je km²) entspricht n.
  Ist die Fahrzeugdichte n groß (in der Stadt), so folgt, dass die Geschwindigkeit v klein wird.
  Ist die Fahrzeugdichte n klein (außerhalb), so kann schneller gefahren werden.
  Auf einer leeren Autobahn (kleine Verkehrsdichte) kann schneller gefahren werden als auf einer vollen Autobahn.

3) Wie groß ist die Dichte n der freien Elektronen?

Wir nehmen der Einfachheit halber an, dass jedes Kupferatom ein freies Elektron zur Leitung bereitstellt.

3.1) Wie viele Atome / freie Elektronen sind in einem Kupferdraht?

Die Chemie hilft uns ein wenig weiter:

Kupfer hat die Atommasse 64 (vgl. Periodensystem der Elemente).
Dies bedeutet, dass 1 Mol Kupfer die Masse 64 g hat.
In einem Mol befinden sich aber immer 6,02 * 10²³ Atome (Avogadro-Zahl).

Damit befinden sich in 64 g Kupfer also 6,02 * 10²³ Atome / freie Elektronen.

3.2) Welches Volumen nehmen 64 g Kupfer ein?

Hier erinnern wir uns an den Anfangsunterricht in Physik: Masse m und Volumen V sind über die Dichte ρ verknüpft. Es gilt:

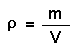
Löst man nach V auf, so ergibt sich mit der Dichte von Kupfer (ρ = 8,9 g / cm³):

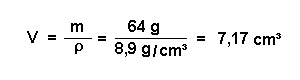
Dies bedeutet nun, dass in 7,17 cm³Kupfer also 6,02 * 10²³ freie Elektronen sind.

3.3) Damit können wir die Elektronendichte n berechnen...

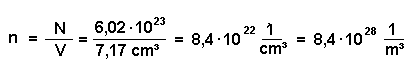
3.4) ... und die Bewegungsgeschwindigkeit der Elektronen abschätzen:

Nehmen wir einen typischen Draht an (Querschnittsfläche 1 mm²) und eine typische Stromstärke (1 A) so ergibt sich als Abschätzung der Bewegungsgeschwindigkeit von Elektronen in Drähten:

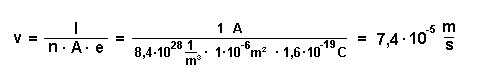
Na, war Dein Tipp in etwa richtig?! Elektronen bewegen sich in Drähten wirklich im "Schneckentempo"! Die Größenordnung beträgt etwa nur 1/10 mm je Sekunde!

4) Warum wir die Geschwindigkeit vielleicht falsch einschätzen:

4.1) Starten die Elektronen erst, wenn ich den Schalter schließe?

Manche denken, dass die Elektronen erst vom Minuspol der Quelle "loslaufen", wenn man einen Schalter schließt. Dann müsste es doch - bei 1/10 mm je Sekunde - einige Zeit dauern, bis eine Lampe aufleuchtet, die Lampe leuchtet aber doch sofort!

Der Denkfehler liegt darin, dass sich ja schon viele freie Elektronen im Draht befinden. Zwar sind sie bei normalen Temperaturen nicht in Ruhe, sondern bewegen sich regellos in alle Raumrichtungen, ein gerichteter Strom entsteht dadurch aber nicht. Erst wenn der Schalter geschlossen wird, baut sich im Leiter ein elektrisches Feld auf und die Elektronen bewegen sich dadurch mit der oben hergeleiteten Geschwindigkeit in Richtung Pluspol der Quelle.

Stelle Dir als (vereinfachtes) Modell einem langen Stau vieler Autos vor einer Baustellenampel vor:
Zeigt die Ampel "rot" (Schalter offen) stehen die Autos. Schaltet die Ampel auf "grün" (Schalter geschlossen) dann fährt die ganze Schlange langsam an. An einem Punkt 50 m vor der Ampel (entspricht der Lampe) sind dann auch sofort Autos, die langsam vorbeifahren. Welche Autos dies sind, ist dabei gleichgültig.

4.2) Wann hört mich mein Partner in Hamburg, den ich von Stuttgart aus anrufe?

Überlegt man so wie oben, dass die Elektronen erst dann "loslaufen", wenn gesprochen wird, dann würden sie für die 535 km lange Strecke Stuttgart-Hamburg folgende Zeit benötigen:

t = s / v = 535 km / 1*10^-4 m/s = 535000 m / 1*10^-4 m/s = 5,35*10⁹ s = 1,48*10⁶ h = 6,13*10⁴ d (Tage) = 169,6 a (Jahre)

Dies würde mein Telefonpartner nie erleben, er wäre inzwischen garantiert gestorben!

Aber auch hier sind die Elektronen ja schon überall in der Leitung!

Wir müssen unterscheiden zwischen der Geschwindigkeit der Elektronen und der Geschwindigkeit des Signals. Die Elektronen bewegen sich dabei praktisch nicht, denn das Sprachsignal ist ja eine Wechselspannung - sie würden sich so höchstens ganz leicht hin- und herbewegen. Die Sprachinformation hingegen bewegt sich praktisch mit Lichtgeschwindigkeit durch den Leiter - und mein Partner in Hamburg hört mich "sofort". Dass die beiden Dinge nicht unbedingt etwas miteinander zu tun haben, könnte man sich an folgendem Modell überlegen: Viele Leute stehen in einer langen Menschenkette, um für Frieden in der Welt zu demonstrieren. Da erfährt der erste in der Schlange vom Ausbruch eines Krieges irgendwo in der Welt. Er gibt die Information - ähnlich wie bei der "stillen Post" - an die Person neben ihm weiter, diese wieder an den nächsten, usw. So gelangt die Information "wie ein Laufffeuer" schließlich ans andere Ende der Menschenkette, ohne dass sich dabei ein Demonstrant auch nur einen Zentimeter bewegen muss! (Das Foto von Udo Leuschner zeigt die Menschenkette beim Protest gegen die Stationierung amerikanischer Mittelstreckenraketen 1983 nahe Göppingen.)

4.3) Bei der Schallleitung ist es auch so.

Ein weiteres ähnliches Beispiel ist die Schallleitung in Luft. Dabei bewegt sich auch kein Luftmolekül vom Sprecher zum Ohr des Zuhörers, sondern die Luftmoleküle geraten in Schwingungen und geben die Schwingung an die nächsten Luftmoleküle weiter. So kann sich die Schallinformation ausbreiten, ohne dass sich die Luftmoleküle dabei sehr bewegen.

Vergleiche dazu auch die Simulation auf der Seite Ausbreitung einer mechanischen Längswelle

5) Aufgaben zur Vertiefung:

(1)
Edwin Hall verwendete zum Nachweis des von ihm entdeckten Effekts ein dünnes Goldband.

• War das Material eine gute Wahl?
• Ermittle die Driftgeschwindigkeit von Elektronen in Gold für die gleichen Parameter (Stromstärke I = 1 A , Fläche A = 1 mm²).

(2)
In einem Halbleiterplättchen (d = 5 mm, Dicke b = 1 mm) misst man eine Hallspannung von 100 mV. Die Stärke des Stroms durch das Plättchen beträgt 50 mA und es wirkt ein Magnetfeld der Stärke 0,2 T senkrecht zum Plättchen.

• Wie groß ist die Driftgeschwindigkeit v der Elektronen im Halbleitermaterial?
• Wie groß ist die Dichte n der freien Elektronen?
• Vergleiche Deine Ergebnisse mit den Werten für Kupfer.

Klaus-Dieter Grüninger, Landesbildungsserver
Grafiken: Grüninger, Fotos: Leuschner(1), Grüninger(1)