Lissajous-Figuren
Für die Wiedergabe der Simulationen auf dieser Seite benötigt
man die Java-Runtime-Environment. Das Laden und Aktivieren der Java-Applets benötigt einen
Augenblick. Bitte nicht "Start" klicken, bevor das Applet
vollständig geladen ist. |
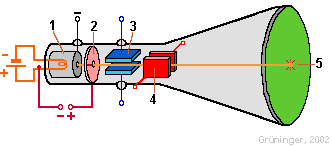 |
Legt man an die beiden Ablenkplattenpaare (3) und (4) einer
braunschen Röhre (eines Oszilloskops) sinusförmige
Wechselspannungen an, dann ergeben sich je nach dem Verhältnis der
beiden Frequenzen, der Amplituden und der Phasenlage einfache - oder auch
komplizierte - geometrische Figuren. Wie diese Figuren entstehen, kannst Du hier virtuell ausprobieren. |
Arbeite dazu einfach zunächst einmal die Fragen
und Aufgaben (unterhalb des Applet) der Reihe nach durch.
Natürlich kannst (und sollst) Du anschließend mit dem
Applet auch noch ein wenig herumspielen, das macht Spaß!
| Mit "schneller" und "langsamer" kann man die
Geschwindigkeit beeinflussen, mit der die Simulation abläuft.
Natürlich kann man sie mit "Pause" jederzeit stoppen. Mit den
Pfeiltasten kann man die Simulation in Einzelschritten vor oder zurück
laufen lassen. Die Wahl der Frequenzen und Amplituden geschieht durch Eintrag in die entsprechenden Felder. |
Fragen und Aufgaben:
1. Erste Erfahrungen mit dem Applet.
a) Klicke zunächst "Start".
- Wie bewegt sich der Elektronenstrahl?
b) Verändere für die y-Richtung nacheinander die Amplitude (zwischen 1 und 30) und die Frequenz (zwischen 0 und 500) durch Eintragen von anderen Werten.
- Wie wirkt sich das auf die Bewegung des Elektronenstrahls aus?
c) Aktiviere nun das Kontrollkästchen bei "Zeige y-Spannung". Der zeitliche Verlauf der Spannung an den Kondensatorplatten für die y-Ablenkung (3) wird nun angezeigt. Klicke wieder "Start".
- Wie ist der zeitliche Verlauf der Spannung an den y-Ablenkplatten?
d) Wähle nun für die Frequenz der y-Ablenkung den Wert "0" und für die Frequenz der x-Ablenkung den Wert "100".
- Wie bewegt sich der Elektronenstahl nun?
e) Klicke nun auch noch das Kontrollkästchen bei "Zeige x-Spannung" an. Und starte die Animation.
- Versuche die Anzeige des Spannung x -Diagramms zu erklären.
- Was passiert, wenn man zusätzlich noch das Kontrollkästchen bei "x-Diagramm drehen" aktiviert?
2) Nun wirken zwei Wechselspannungen gleicher Frequenz.
a) Wähle nun für die beiden Spannungen in x-Richtung und in y-Richtung gleiche Amplituden und trage für beide Wechselspannungen gleiche Frequenzen(z.B. 50 Hz) ein.
- Wie verläuft der Elektronenstrahl nun?
- Erkläre seinen Verlauf! (Klicke dazu evtl. auch die Kontrollkästchen oben rechts an).
- Was musst Du tun, um eine Gerade mit anderer Steigung zu erhalten?
b) Trage nun bei Phasenlage 90 Grad ein. Amplituden und Frequenzen beider Spannungen sind immer noch gleich.
- Wie verläuft der Elektronenstrahl jetzt?
- Was verändert sich an den Spannungen, wenn die Phasenlage verändert wird?
- Wenn die y-Spannung nun sinusförmig ist, welchen Verlauf hat die x-Spannung?
- Wie sieht der Verlauf bei einer Phasenlage von 45 Grad aus?
3) Die beiden Wechselspannungen haben unterschiedliche Frequenzen
a) Wähle für die beiden Wechselspannungen nun gleiche Amplituden aber ein Frequenzverhältnis von 2:1 also z.B. 100 Hz für x-Spannung und 50 Hz für y-Spannung. Der Phasenwinkel ist zunächst 0 Grad.
- Wie sieht die Figur, den die Elektronenstahlen nun schreiben, aus?
- Was geschieht, wenn die Frequenz der y-Spannung doppelt so groß wie die der x-Spannung ist?
- Was ändert sich, wenn man als Phasenlage 90 Grad eingibt?
- Wie sieht die Figur bei einer Phasenlage von 45 Grad aus?
b) Wähle nun ein Frequenzverhältnis von 3:1 also z.B. 300 Hz und 100 Hz.
- Wie sehen die Kurven nun aus?
- Probiere auch andere geradzahlige Frequenzverhältnisse aus.
Experimentiere nun zusätzlich auch noch mit der Phasenlage.
- Wie muss man diese wählen, damit der Strahl den Buchstaben "N" schreibt?
c) Wähle nun die Frequenzen so, dass die beiden Frequenzen kein ganzzahliges Vielfaches mehr voneinander sind.
- Welchen Einfluss hat dies auf die Lissajous-Figuren?
Diese Fragen gibt es auch als Arbeitsblatt:
| Im Format Microsoft-Word: lissajous.doc |
| Im Format Acrobat-Reader (PDF):lissajous.pdf |
Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:
Sie müssen dazu die gepackte Datei (lissajous.zip) herunterladen und in
ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder.
Die nötigen Java-Achive sind ebenfalls enthalten.
Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.
| Die Datei herunterladen : lissajous.zip |
Nutzungsbedingungen:
Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern
gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und
Kollegen weitergeben.
Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der
ausdrücklichen Zustimmung.
Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang
Christian und Mario Belloni vom Davidson College, USA
|


