Virtuelles Oszilloskop.
Für die Wiedergabe der Simulationen auf dieser Seite benötigt
man die Java-Runtime-Environment. Das Laden und Aktivieren der Java-Applets benötigt einen
Augenblick. Bitte nicht "Start" klicken, bevor das Applet
vollständig geladen ist. |
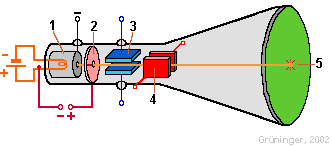 |
Eine braunsche Röhre oder - auch Oszilloskop - ist ein sehr schönes und vielseitiges Messinstrument. Mit ihm kann man Spannungen und Frequenzen messen und auch beurteilen, ob z.B. Gleichspannungen wirklich "sauber" sind, d.h. ob die Spannung wirklich exakt gleich bleibt. Mit dem Applet auf dieser Seite kannst Du die Grundfunktionen eines Oszilloskops kennen lernen und erforschen. |
Bei "Einstellungen Signal", kann man beeinflussen,
wie die Spannung aussieht, die man an das Oszilloskop "anlegt". Die
Spannung und die Frequenz einer Wechselspannung kann hier eingestellt werden.
Bei "Einstellungen Oszilloskop" kann man den
Verstärkungsfaktor und die Zeitablenkung verändern. |
Fragen und Aufgaben:
1. Das Oszilloskop als Spannungsmessgerät
Klicke mit den Grundeinstellungen einfach "Start". Der Strahl
läuft von links nach rechts.
Trage nun bei den Signaleinstellungen als Spannung "2" ein- Du hast
nun eine Gleichspannung von 2 V gewählt.
- Wo verläuft der Strahl nun?
Wähle bei den "Einstellungen Oszilloskop" als y-Amplitude die Optionen 0,5 und 2 aus.
- Was verändert sich an der Ablenkung des Strahls?
- Welche Funktion hat also die Auswahl von y-Amplitude?
- Wie weit wird der Strahl wohl abgelenkt, wenn Du bei y-Amplitude "10" einstellst und die Gleichspannung 30 V beträgt (Einstellen im Feld "Spannung" bei "Einstellungen Signal")?
Klicke das Kontrollkästchen bei "Umpolen" an.
- Wie wird der Strahl nun abgelenkt?
Klicke bei den "Einstellungen Oszilloskop" das Kontrollfeld "Taste Ground gedrückt".
- Was passiert?
- Welche Funktion hat also die "Ground-Taste" bzw. der "Ground-Schalter"?
2. Das Oszilloskop als Frequenzmessgerät
Drücke die "Ground-Taste" und klicke auf Start. Verändere diesmal die Einstellungen bei "Zeitkonstante".
- Wie lange benötigt der Strahl in Einstellung 100 ms / cm von links nach rechts?
- Wie lange braucht er dann für 1 cm?
- Wie viel ist diese Zeit in Millisekunden?
- Wie lange benötigt der Strahl in Stellung "50" für den ganzen Bildschirm / für 1 cm?
- Wie sind die entsprechenden Werte für Stellung "20"?
- Was bestimmt man also mit dem Schalter "Zeitkonstante"?
Stelle nun ein Signal mit Spannung 2 V und Frequenz 50 Hz ein. Es entspricht
einer Wechselspannung von 2 V Scheitelspannung aus unserem
Wechselspannungsnetz.
Klicke nun unbedingt "Zeitlupe" an.
Stelle als Zeitkonstante 20 ms / cm ein.
- Welche Wegstrecke in x-Richtung nimmt eine Periode ein?
- Wie lange dauert also eine Periode?
- Prüfe mit T=1 / f nach!
Verändere nun die Zeitkonstante auf 10 ms/ cm.
- Wie viele cm auf dem Schirm in x-Richtung nimmt eine Periode nun ein?
- Was ist anders als vorher?
Setze die Frequenz bei Signal nun auf 10 Hz.
- Welche Wegstrecke in x-Richtung nimmt eine Periode nun ein?
- Wie lange dauert eine Periode?
- Prüfe wieder mit T=1 / f nach!
| Die folgende Betrachtung hat nicht unbedingt etwas mit dem Oszilloskop zu tun, sondern ist nur ein Effekt der digitalen Simulation eines Oszilloskops auf dem Bildschirm. Was hier passiert, ist aber für die digitale Messwerterfassung wichtig. |
3. In der Simulation passieren seltsame Effekte / Probleme digitalen Abtastens - Shannon -Theorem.
Die Simulation ist nicht so perfekt wie ein echtes
Oszilloskop!
Sie kann nur maximal 100 Bilder pro Sekunde darstellen.
Wenn Du also als Zeitkonstante 10 ms / cm auswählst, dann benötigt
der Stahl 100 ms (=0,1 s) für die 10 cm Bildschirmbreite.
In diesen 0,1 s können bei 100 Bildern pro Sekunde dann 10 Bildpunkte /
Spannungswerte errechnet und dargestellt werden.
Gib nun als Ablenkung 10 ms / cm und lasse die Darstellung in Echtzeit ausgeben (also Zeitlupe nicht gedrückt). Wähle als Frequenz des Signals zunächst 10 Hz.
- Findest Du die 10 berechneten Punkte in der Darstellung, die einfach verbunden wurden?
Verdopple die Frequenz nun auf 20 Hz. Hier siehst Du die Punkte noch deutlicher. Die Kurve wird deutlich "kantig".
- Wie viele Messpunkte werden nun während einer Periode erfasst?
Verdopple die Frequenz nochmals auf 40 Hz. Lasse die Kurve einmal mit und einmal ohne Zeitlupe darstellen.
- Kannst Du den seltsamen Effekt erklären?
- Wie viele Messpunkte werden nun ohne Zeitlupe während einer Periode erfasst?
- Mit Zeitlupe werden 10 mal so viele Messpunkte erfasst. Wie viele sind das dann?
Du hast gesehen, dass man mit 10 Messpunkten pro Periode ein Signal noch ganz brauchbar darstellen kann. Auch mit 5 Messpunkten pro Periode geht es gerade noch so. Bei 40 Hz (das sind 2,5 Messpunkte pro Periode) gibt es nur noch "Gezappel" - eine Sinusschwingung ist nicht mehr klar zu erkennen, hier wird es schon kritisch. Wählt man die Frequenz noch höher (50 Hz und mehr - entspricht weniger als zwei Messpunkte pro Periode) bekommt man nichts Brauchbares mehr.
| Um ein Signal sinnvoll erfassen und darstellen zu können, muss man pro
Periode mindestens etwa 3 Messpunkte erfassen. Man nennt diese Tatsache das Shannon-Theorem. |
Dies ist dann z.B. für alle digitalen Messwerterfassungen
wichtig.
In einer Soundkarte wird im Normalfall das Stereosignal 44100 mal pro
Sekunde abgetastet. Pro Kanal sind das dann 22050 Messwerte, die in jeder
Sekunde erfasst werden, die Zeit zwischen zwei Messungen ist dann also 1/22050
s oder etwa 4,5*10-5 s.
Hat man ein Tonsignal von 1000 Hz (das ist eine Periodendauer von 1*10-3 s)
dann werden während einer Periode also 1*10-3 s / 4,5*10-5 s = 22 Messwerte
erfasst. Das reicht für eine gute Erfassung aus. Bei 10000 Hz sind das dann nur noch 1/10 davon, also etwa 2,2. Hier wird es schon kritisch.
Würde man Mono aufzeichnen, dann wäre es der doppelte Wert - also etwa 4,5 Messungen je Periode. Dann funktioniert das noch bis etwa 10.000 Hz sauber.
Man sieht also: handelsübliche Soundkarten mit einer Abtastrate von 44100 Samples pro Sekunde (Messpunkte je Sekunde) tasten in Stereo ein Signal nur bis etwa 10000 Hz wirklich sauber ab. In der Praxis genügt das.
Um einen Signalverlauf brauchbar exakt erfassen zu können, muss die Abtastrate etwa 2,5 mal so groß sein, wie die höchste zu erwartenden Frequenz. Möchte man also ein Tonsignal im gesamten für den Menschen hörbaren Bereich (bis 20.000 Hz) wirklich sauber abtasten, müsste die Soundkarte eine Samplerate von 100.000 pro Sekunde (bei Stereo) haben.
Mehr zum Nyquist-Shannon-Theorem ( auch WKS-Sampling-Theorem (für Whittaker-Kotelnikow-Shannon)): ![]() http://de.wikipedia.org/wiki/Nyquist-Shannon-Abtasttheorem
http://de.wikipedia.org/wiki/Nyquist-Shannon-Abtasttheorem
Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:
Sie müssen dazu die gepackte Datei (oszilloskop.zip) herunterladen und in
ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder.
Die nötigen Java-Achive sind ebenfalls enthalten.
Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.
| Die Datei herunterladen : oszilloskop.zip ALT="gepackte Datei" BORDER="0" TITLE="gepackte Datei"> |
Nutzungsbedingungen:
Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern
gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und
Kollegen weitergeben.
Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der
ausdrücklichen Zustimmung.
Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang
Christian und Mario Belloni vom Davidson College, USA
(Copyright Hinweise) |


