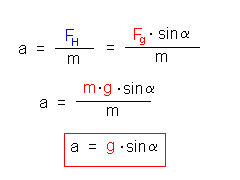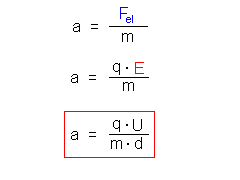Bewegung einer Ladung im Längsfeld und Bewegung an der schiefen Ebene.

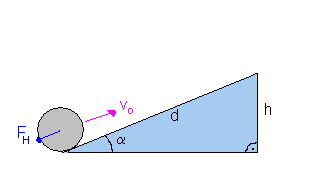
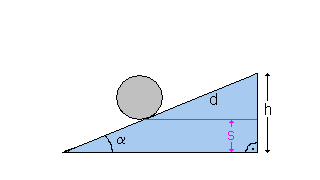
1) Die Schwerkraft und die Hangabtriebskraft.

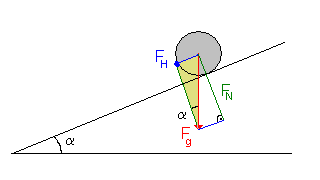Betrachte die im Bild gezeichnete Kugel. Auf sie wirkt die Schwerkraft F_g. Diese bewirkt einerseits, dass die Kugel mit einer gewissen Kraft, der Normalkraft F_N, auf die Unterlage drückt, andererseits wirkt die Hangabtriebskraft F_H, welche die Kugel "den Hang hinunter treibt".

Zwischen der Schwerkraft F_g und der Hangabtriebskraft F_H gilt im linken rechtwinkligen Kräftedreieck (gelb eingefärbt) folgende Beziehung:
Schwerkraft und Hangabtriebskraft

Wobei α auch der Neigungswinkel der schiefen Ebene ist.
.

Da bei der schiefen Ebene der Neigungswinkel α und die Schwerkraft F_g konstant sind, ist auch die Hangabtriebskraft F_H konstant.

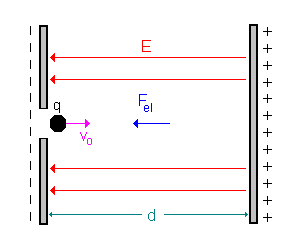
2.1.) Bewegung die schiefe Ebene hinunter / Bewegung der Ladung +q in Richtung des elektrischen Feldes.

Bewegung der Kugel eine schiefe Ebene hinunter	Bewegung einer Ladung +q in Feldrichtung (nach links)

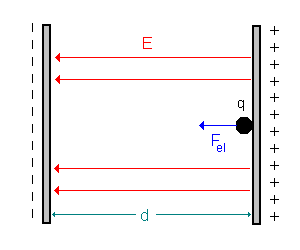Kraft, Bewegung	Kraft, Bewegung
Die Hangabtriebskraft F_H ist konstant. Die Beschleunigung a ist daher auch konstant. Für sie gilt: Die Kugel führt eine gleichmäßig beschleunigte Bewegung aus. Die Größe der Beschleunigung lässt sich durch den Hangwinkel α verändern, eine große Neigung führt zu einer großen Beschleunigung.	Die elektrische Feldkraft F_el ist konstant. Die Beschleunigung a ist daher auch konstant. Für sie gilt: Die Ladung führt eine gleichmäßig beschleunigte Bewegung aus. Die Größe der Beschleunigung lässt sich durch die angelegte Spannung U verändern, eine große Spannung führt zu einer großen Beschleunigung.

Das kennst du aus dem Alltag, wenn du mit dem Fahrrad oder mit den Ski einen Berg hinunter fährst:

Die Lageenergie nimmt ab und die Bewegungsenergie nimmt zu - du wirst also schneller.
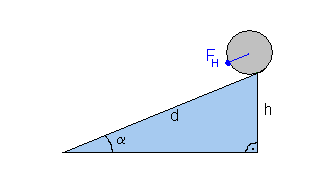
Welche Geschwindigkeit du am Fuß des Hangs erreichst, hängt davon ab, wie steil der Hang ist (wie groß also die Hangabtriebskraft ist) und wie lange der Hang ist (Strecke d).
An einem langen und steilen Hang erreichst du unten eine große kinetische Energie und damit eine große Geschwindigkeit.

Energieumwandlung	Energieumwandlung
Zunächst hat die Kugel nur Lageenergie (potentielle Energie) Für sie gilt: 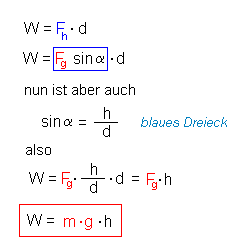Es gilt der Energieerhaltungssatz: Diese Energie wird am bis zum Boden (Nullniveau) komplett in kinetische Energie umgewandelt. Es gilt: *W_kin = 1/2 m * v² = m * g * h**.	Zunächst hat die Ladung nur potentielle Energie Für sie gilt: 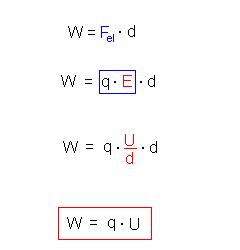Es gilt der Energieerhaltungssatz: Diese Energie wird bis zur linken Platte (Potentialnullpunkt) komplett in kinetische Energie umgewandelt. Es gilt: *W_kin = 1/2 m * v² = q * U**.

2.2.) Bewegung den Hang hinauf / Ladung +q im elektrischen Gegenfeld.

Bewegung der Kugel eine schiefe Ebene hinauf	Bewegung einer Ladung +q entgegen der Feldrichtung (nach rechts)

Kraft, Bewegung	Kraft, Bewegung
Die konstante Hangabtriebskraft ist die gleiche wie in 2.1.) Sie wirkt der Bewegung der Kugel entgegen. Die Kugel führt eine Bremsbewegung mit konstanter Verzögerung a aus. Diese ist so groß wie die Beschleunigung in 2.1.).	Die konstante elektrische Feldkraft ist die gleiche wie in 2.1.) Sie wirkt der Bewegung der Ladung entgegen. Die Ladung führt eine Bremsbewegung mit konstanter Verzögerung a aus. Diese ist so groß wie die Beschleunigung in 2.1.).

Das kennst du aus dem Alltag, wenn du mit dem Fahrrad (ohne weiter zu treten) einen Berg hinauf fährst:

Die Bewegungsenergie nimmt ab und die Lageenergieenergie nimmt zu - du wirst also langsamer, kommst dafür aber den Hang hinauf..
Ob du einen Hang gut, gerade eben noch so, oder auch gar nicht schaffst, hängt von deiner Anfangsgeschwindigkeit und damit von deiner kinetischen Energie am Fuß des Hangs ab.
Natürlich spielt dabei auch Steigungs des Hangs (letztlich die Größe der Hangabtriebskraft, die dich nun bremst) und die Länge des Hangs eine Rolle.

Energieumwandlung

Auf dem Weg nach oben nimmt die kinetische Energie der Masse ab und die potentielle Energie (Lageenergie, Höhenenergie) nimmt zu.

Auf dem Weg zur positiv geladenen Platte nimmt die kinetische Energie der Ladung ab und die potentielle Energie nimmt zu.

a) Welche kinetische Energie muss die Kugel haben, damit sie den höchsten Punkt des Hangs gerade so erreicht?

a) Welche kinetische Energie muss die Ladung haben, damit sie die rechte Kondensatorplatte gerade knapp erreicht?

Energie	tiefster Punkt (unten)	höchster Punkt (oben)
kin. Energie	1/2 * m * v²	0
Lageenergie	0	m * g * h

Die Kugel erreicht - wenn man die Reibung vernachlässigt - den höchsten Punkt gerade eben so, wenn sie mit der Geschwindigkeit v unten startet, die sie in 2.1.) unten erreicht hat.
Es gilt der Energieerhaltungssatz.
Im höchsten Punkt am Ende der Bahn kehrt sie um und führt die Bewegung aus 2.1.) aus, d.h. sie kommt wieder mit der gleichen Geschwindigkeit unten an, mit der sie gestartet ist.

Energie	linke Platte	rechte Platte
kin. Energie	1/2 * m * v²	0
potentielle Energie	0	q * U

Die Ladung erreicht die rechte Platte gerade eben so, wenn sie mit der Geschwindigkeit v an der linken Platte startet, die sie in 2.1.) dort erreicht hat.
Es gilt der Energieerhaltungssatz.
An der rechten Kondensatorplatte kehrt sie um und führt die Bewegung aus 2.1.) aus, d.h. sie kommt wiedermit der gleichen Geschwindigkeit an der linken Platte an, mit der sie gestartet ist.

b) Die kinetische Energie bei Start ist größer als in a)

b) Die kinetische Energie beim Start ist größer als in a)

Startet die Kugel mit einer größeren Geschwindigkeit, hat sie zu Beginn auch eine größere kin. Energie.
Wenn sie den höchsten Punkt der schiefen Ebene erreicht, hat sie also noch kin. Energie übrig:
(kin. Energie (oben) = Anfangsenergie(unten) - m* g * h)

Startet die Ladung mit einer größeren Geschwindigkeit, hat sie zu Beginn auch eine größere kin. Energie.
Wenn sie die rechte Kondensatorplatte erreicht, hat sie also noch kin. Energie übrig:
(Energie an der rechten Platte = Anfangsenergie (linke Platte) - q* U) und prallt auf diese auf.

c) Die kinetische Energie beim Start ist kleiner als in a)

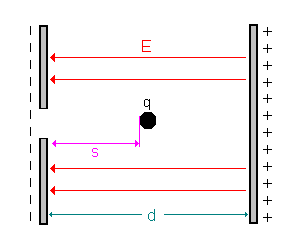
Die Kugel erreicht nun den oberen Punkt der schiefen Ebene nicht mehr, sondern kehrt schon vorher um.

Die Ladung erreicht nun die rechte Kondensatorplatte nicht mehr, sondern kehrt schon vorher um.

Ist die kinetische Energie beim Start nur halb so groß wie in a), so kommt die Kugel auch nur die halbe Ebene hinauf bis zur Höhe s = h / 2 und kehrt dort um.

Ist die kinetische Energie beim Start nur 1/4 so groß wie in a), so kommt die Kugel auch nur bis zur Höhe s = h / 4.
Die Steighöhe s ist also zur Anfangsenergie W_kin = 1/2 * m * v² proportional.

Ist die kinetische Energie beim Start nur halb so groß wie in a), so kommt die Ladung nur bis genau zur Mitte des Kondensators also bis s = d / 2 und kehrt dort um.

Ist die kinetische Energie beim Start nur 1/4 so groß wie in a), so kommt die Ladung nach s = d / 4 zur Ruhe und kehrt dann um.
Die im Kondensator zurückgelegte Wegstrecke s ist also zur Anfangsenergie W_kin = 1/2 * m * v² proportional.

Grüninger, Landesbildungsserver, 2011