Bewegung einer Ladung im Längsfeld und senkrechter Wurf.

1) Drehen erhöht manchmal den Durchblick!

Auf dieser Seite wurde gezeigt, dass man bei der Bewegung von Ladungen im Plattenkondensator den Einfluss der Schwerkraft in der Regel vernachlässigen kann.
(Bei den weiter unten besprochenen Rechenbeispielen sind die elektrischen Kräfte um einen Faktor 100 größer als die Schwerkraft).

Man kann daher die Bewegung einer Ladung im Längsfeld um 90° drehen und erhält folgende analoge Darstellungen:

	Ladung im E-Feld waagrecht betrachtet		Ladung im E-Feld senkrecht betrachtet
a) gleichmäßig beschleunigte Bewegung		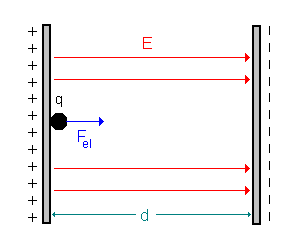Drehen um 90° im Uhrzeigersinn
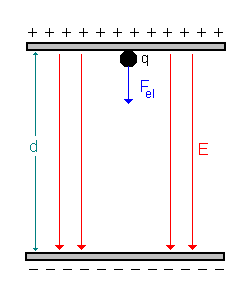b) konstant verzögerte Bewegung		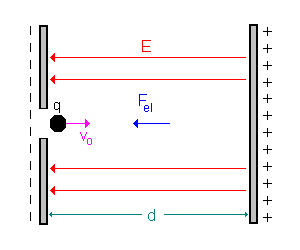Drehen um 90° gegen den Uhrzeigersinn

Die rechten Darstellungen erinnern an den senkrechten Wurf :

untere Darstellung (b): die gebremste Steigbewegung
obere Darstellung (a) : der freie Fall (bzw. den zweiten Teil des senkrechten Wurfs)

So lassen sich die Bewegungen von Teilchen im Längsfeld völlig analog zum senkrechten Wurf der Mechanik betrachten. Dabei wird vom Luftwiderstand abgesehen.

Diese Parallele wird auf dieser Seite näher untersucht.

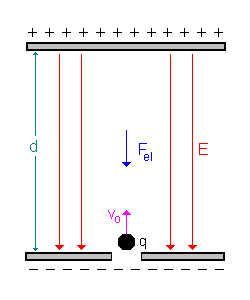
2.1.) Freier Fall / Bewegung einer Ladung +q in Richtung des elektrischen Feldes.

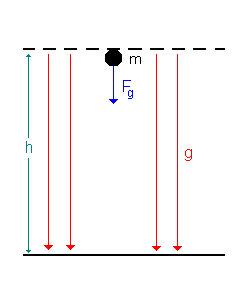
Wir betrachten bei der Parallele zunächst den zweiten Teil des senkrechten Wurfes, also den Teil bei dem der Körper vom höchsten Punkt seiner Bahn wieder zum Ausgangspunkt zurückfällt.

Freier Fall einer Masse m	Bewegung einer Ladung +q


Feld, Kraft, Bewegung	Feld, Kraft, Bewegung
Das Gravitationsfeld in der Nähe des Erdbodens ist homogen. Die Fallbeschleunigung g hat überall den gleichen, konstanten Wert. Auf die Masse m wirkt eine konstante Schwerkraft F_g = m * g. Die Masse führt eine gleichmäßig beschleunigte Fallbewegung aus.	Das el. Feld im Plattenkondensator ist homogen. Die el. Feldstärke E hat überall den gleichen, konstanten Wert. Auf die Ladung q wirkt eine konstante el. Kraft F_el = q * E. Die Ladung führt eine gleichmäßig beschleunigte Bewegung aus.

Energieumwandlung	Energieumwandlung
Die Masse m hat zunächst nur potentielle Energie. *W = F_g h = m * g * h Auf dem Weg zum Erdboden nimmt die potentielle Energie ab und die kinetische Energie nimmt zu. Es gilt der Energieerhaltungssatz. Am Erdboden ist die potentielle Energie 0, dort ist das Nullniveau. Es gilt W_kin = 1/2 * m * v² = m * g * h**.	Die Ladung q hat zunächst nur potentielle Energie. *W = F_el d = q * E * d Auf dem Weg zur negativen Kondensatorplatte nimmt die potentielle Energie ab und die kinetische Energie nimmt zu. Es gilt der Energieerhaltungssatz . An der negativen Kondensatorplatte ist die potentielle Energie 0, dort ist das Nullniveau, der Potentialnullpunkt. Es gilt W_kin = 1/2 * m * v² = q * E * d**.

Eine typische Aufgabe: Eine Masse m = 0,1 kg fällt aus einer Höhe h = 1,0 m ohne Reibung nach unten. Welche Energie und welche Geschwindigkeit hat sie am Boden? Welche Bewegungsenergie und welche Geschwindigkeit hat sie nach halber Fallstrecke? Ergebnisse für g = 10 m/s²: Startenergie und Energie am Boden 1,0 J, Geschwindigkeit am Boden etwa 4,47 m/s. In halber Höhe halbe kinetische Energie (0,5 J), Geschwindigkeit dort 3,16 m/s.	*Eine typische Aufgabe:* Eine kleine Kugel der Ladung q = + 10 nC hat die Masse 1 mg und bewegt sich von der positiven zur negativen Platte eines Plattenkondensators. Die angelegte Spannung ist 1000 V der Plattenabstand ist 10 cm. Mit welcher Energie und welcher Geschwindigkeit trifft sie auf die negative Platte auf? Welche Energie und welche Geschwindigkeit hat sie genau in der Mitte des Plattenkondensators? Ergebnisse: E = U / d = 10 000 V/m. el. Kraft F_el = q * E = 110^-4 N , Energie bis zur negativen Platte: W = q E * d = 110^-5 J. Geschwindigkeit dort 4,47 m/s In halber Höhe halbe kinetische Energie (0,5 10^-5J), Geschwindigkeit dort 3,16 m/s.

Hier finden Sie die ausführliche Lösung der Aufgaben.

Die beiden Aufgaben sind völlig analog. In beiden Fällen bekommt man als Ergebnis, dass die kinetische Energie des Körpers auf halber Strecke genau die Hälfte der Energie ist, die er nach der ganzen Bewegung hat.

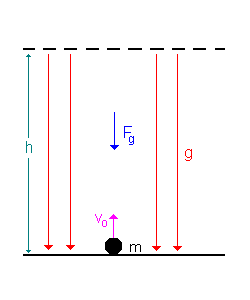
2.2.) Bewegung einer Masse nach oben / Ladung +q im elektrischen Gegenfeld.

Nun betrachten wir den ersten Teil der Bewegung des senkrechten Wurfes und seine Entsprechung im elektrischen Feld.

Bewegung einer Masse m nach oben	Bewegung einer Ladung +q im Gegenfeld
Die Masse m wird mit einer Anfangsgeschwindigkeit v_o nach oben geworfen	Die Ladung q tritt mit einer Anfangsgeschwindigkeit v_o durch eine Öffnung in der Kondensatorplatte in das el. Feld ein.

Es wirkt eine *konstante Schwerkraft F_g = m g der Bewegung der Masse entgegen. Die Masse m führt eine Bremsbewegung mit konstanter Verzögerung** aus. Die Geschwindigkeit der Masse nimmt ab.	Es wirkt eine *konstante el. Kraft F_el = q E der Bewegung der Ladung entgegen. Die Ladung q führt eine Bremsbewegung mit konstanter Verzögerung** aus. Die Geschwindigkeit der Ladung nimmt ab.
Energieumwandlung	Energieumwandlung
Auf dem Weg nach oben nimmt die kinetische Energie der Masse ab und die potentielle Energie (Lageenergie, Höhenenergie) nimmt zu.	Auf dem Weg zur positiv geladenen Platte nimmt die kinetische Energie der Ladung ab und die potentielle Energie nimmt zu.
3 Fälle sind dabei möglich:	3 Fälle sind dabei möglich:
Kann die Masse m die Höhe h erreichen? a) Ist die Anfangsenergie und die Anfangsgeschwindigkeit v_o "genau richtig", wird die Höhe h gerade erreicht (Geschwindigkeit ist dort 0) und die Masse kehrt dort um. b) Sind Anfangsgeschwindigkeit und Anfangsenergie kleiner, dann erreicht die Masse die Höhe h nicht und kehrt vorher um. c) Ist die Anfangsenergie größer, steigt die Masse höher als h und kehrt erst bei größerer Höhe um.	Kann die Ladung q zur positiv geladenen Platte gelangen? a) Ist die Anfangsenergie und die Anfangsgeschwindigkeit v_o "genau richtig", wird die Platte gerade erreicht (Geschwindigkeit ist dort 0) und die Ladung kehrt dort um. b) Sind Anfangsgeschwindigkeit und Anfangsenergie kleiner, dann erreicht die Ladung die positive Platte nicht und kehrt vorher um. c) Ist die Anfangsenergie größer, trifft die Ladung mit einer Restenergie / Restgeschwindigkeit auf die Platte auf.
a) Die "richtige" Höhe	a) Die "richtige" Höhe
Startet die Kugel gerade mit der Geschwindigkeit v_o, die sie beim freien Fall aus der gleichen Höhe h erreicht hat (in der Beispielaufgabe 4,47 m/s), dann erreicht sie bei der verzögerten Bewegung nach oben ebenfalls gerade die Höhe h. Dahinter steckt der Energieerhaltungssatz.	Startet die Ladung gerade mit der Geschwindigkeit v_o, die sie bei der beschleunigten Bewegung beim Plattenabstand d erreicht hat (in der Beispielaufgabe 4,47 m/s), dann erreicht sie bei der Bremsbewegung gerade ebenfalls die andere Platte wieder. Dahinter steckt der Energieerhaltungssatz.
b) Wie hoch kommt die Kugel?	b) Wie weit kommt die Ladung?
Ist die Anfangsgeschwindigkeit kleiner, so wird die Höhe h nicht erreicht. Startet die Kugel z.B. mit v = 3 m/s, so ist ihre kinetische Anfangsenergie W_kin = 1/2 * m * v²=1/2 * 0,1 kg * (3 m/s)² = 0,45 J. Mit dieser Energie kommt sie bis in die Höhe s. Es gilt W_kin(unten) = W_L(oben) = m * g * s. Daraus folgt s = 0,45 m.	Ist die Anfangsgeschwindigkeit kleiner, so wird die Ladung die andere Platte nicht erreichen. Startet sie z.B. mit v = 3 m/s, so ist ihre kinetische Anfangsenergie W_kin = 1/2 * m * v²=1/2 * 1 10^-6 kg (3 m/s)² = 4,5 10^-6 J. Mit dieser Energie kommt sie bis in die Distanz s. Es gilt W_kin(unten) = W_L(oben) = q E * s. Daraus folgt s = 4,5 cm.
c) Welche Geschwindigkeit hat die Kugel in der Höhe h?	c) Mit welcher Geschwindigkeit prallt die Ladung auf der Platte auf?
Ist die Anfangsgeschwindigkeit größer als v_o, so erreicht die Kugel die Höhe h und hat dort noch kin. Energie übrig um noch höher zu steigen. Ist die Anfangsgeschwindigkeit z.B. 6 m/s , so ist die kin. Energie unten 1,8 J. Auf dem Weg bis zur Höhe h werden davon 1,0 J in Lageenergie umgewandelt. Also hat die Kugel dort noch 0,8 J kin. Energie, was einer Geschwindigkeit von 4 m/s entspricht.	Ist die Anfangsgeschwindigkeit größer also v_o, so erreicht die Ladung die gegenüberliegende Platte und hat dann noch eine kinetische Restenergie übrig, so dass sie mit einer bestimmten Geschwindigkeit auf die Platte aufprallt. Ist die Anfangsgeschwindigkeit z.B. 6 m/s, so ist die kin. Energie an der negativen Platte 1,8 * 10^-5 J. Auf dem Weg zur positiven Platte verliert sie 1 * 10^-5 J durch die Bremsbewegung. Beim Aufprall hat sie also noch 0,8 * 10^-5 J Restenergie. Dies entspricht einer Aufprallgeschwindigkeit von 4 m/s.

Natürlich lassen sich die Bewegungen wieder "um 90° zurückdrehen"!
Die 3 Fälle gelten daher auch für die horizontale Bremsbewegung einer Ladung im elektrischen Längsfeld!

Hier finden Sie die ausführliche Lösung der Aufgaben.

Grüninger, Landesbildungsserver, 2011