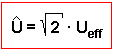Der Effektivwert einer sinusförmigen Wechselspannung.
Das folgende Java-Applet soll die Leistungsabgabe an ein Gerät (eine Glühlampe) im Gleichspannungs- und Wechselspannungskreis miteinander vergleichen und den Begriff des "Effektivwerts einer Wechselspannung" einführen.
| Ein Klick auf "Start" im jeweiligen Bedienfeld stellt im
oberen Diagramm den Verlauf von Spannung und Stromstärke, im unteren
Diagramm den Verlauf der an der Lampe abgegebenen Leistung dar. Mit "Pause" kann man die Darstellung anhalten und mit "Start" fortsetzen. "Reset" löscht die jeweilige Darstellung. Die abgegebene Leistung im Gleichspannungskreis wird auch im Leistungsdiagramm des Wechselstromkreises zu Vergleichszwecken eingetragen. Werden in den Auswahlfeldern unter dem Applet Änderungen vorgenommen, werden beide Animationen automatisch zurückgesetzt. Man kann den Widerstandswert der Lampe ändern (ändert gleichzeitig in beiden Animationen). Der Scheitelwert der Wechselspannung Û kann verändert werden, ebenso die Frequenz der Wechselspannung. Der Wert der Gleichspannung kann frei eingestellt werden. |
Beginne nicht mit der Arbeit, bevor die beiden Schaltkreise (oben) sichtbar sind, und die vier Diagrammfelder vollständig geladen wurden.
Fragen / Aufgaben.
(1) Gleichstromkreis.
(1) a) Klicke "Start" (Bedienfeld links) und beobachte
die Lampe im Schaltbild
- Was kann man über das Leuchten der Lampe aussagen?
b)Belasse zunächst die Voreinstellungen. ( 5 V und 5 Ohm )
Beobachte den Verlauf der Spannung, der Stromstärke und der abgegebenen
Leistung im Gleichstromkreis.
- Welchen Wert hat die Spannung?
- Welchen Wert hat die Stromstärke?
- Wie kann man diesen Wert berechnen?
- Welchen Wert hat die abgegebene Leistung? - Vergleiche mit dem im Diagramm angezeigten Wert.
c) Abhängigkeit der Leistung P von der Spannung U:
Belasse den Widerstand auf 5 Ohm und verdopple die Spannung auf 10 V.
- Wie verändert sich die Stromstärke?
- Wie verändert sich die abgegebene Leistung ?
- Wie ist der Zusammenhang zwischen der Spannung der Quelle und der
abgegebenen Leistung?
(Vergleiche Leistung bei 5V und bei 10V)
d) Abhängigkeit der Leistung P vom Widerstand R:
Belasse die Spannung auf 10 V. Wähle als Widerstand der Lampe nun 10
Ohm ( verdopple ihn also) .
- Wie ändert sich die Stromstärke?
- Wie ändert sich die abgegebene Leistung?
- Welchen Zusammenhang zwischen Widerstand und Leistung kann man angeben?
(Vergleiche Leistung bei 10V und 5Ohm Widerstand bzw. 10 Ohm Widerstand) - Welche Energiemenge wird in 40 ms an die Lampe abgegeben?
- Wie ist diese Energiemenge im Leistungs-Zeit-Diagramm ablesen?
Sicher bist du auch auf folgende Lösung gekommen: |
(2) Wechselstromkreis.
a) Belasse den Widerstand der Lampe auf 10 Ohm.
Klicke im Bedienfeld des Wechselspannungskreises (rechts)
"Start" und beobachte die Lampe.
- Warum "blinkt" die Lampe?
- Welchen Wert haben Spannung und Stromstärke, wenn die Lampe "hell" leuchtet?
- Welchen Wert haben Spannung und Stromstärke, wenn die Lampe nicht leuchtet?
b) Leistungsdiagramm P(t) und Verlauf von Spannung U(t) und Stromstärke I(t).
- Wann ist die abgegebene Leistung maximal / minimal?
- Wie viele Maxima der Leistung gibt es während einer Periode der Wechselspannung?
- Warum verläuft das Leistungsdiagramm nur im positiven Bereich?
- Kannst du eine Gleichung für P(t) angeben, wenn die Spannung U(t) und die Stromstärke I(t) sinusförmig ist?
(3) Vergleich der beiden Stromkreise.
Offenbar wird im Gleichstromkreis stets eine konstante,
unveränderliche Leistung an das Lämpchen abgegeben. Die Linie für die Leistung aus dem Gleichspannungs-Leistungsdiagramm (links) wird als violette Linie ins Leistungsdiagramm der Wechselspannung (rechts) übertragen. |
Der Lampenwiderstand in beiden Schaltungen ist nun immer noch 10
Ohm.
Lasse die Darstellung der Wechselspannung ablaufen. (50 Hz,
Û = 14,14 V)
Wähle als Spannung der Gleichspannungsquelle (Ueff)
nacheinander 8 V, 10V , 12 V.
Leistungsdiagramm der Wechselspannung:
Vergleiche die Flächen der hellblauen "Spitzen",
die oberhalb der violetten Linie liegen mit den weißen
"Spitzen" unterhalb dieser Linie.
- Bei welcher Gleichspannung Ueff geben beide Quellen im zeitlichen Mittel gleiche Leistung ab?
- Was kann man bei der "richtigen" Spannung über die Flächen der o.g. "Spitzen" aussagen.
Wir vergleichen die Leistungsabgaben einer Wechselspannungsquelle im zeitlichen Mittel mit der Leistungsabgabe einer Gleichspannungsquelle. Bei einer sinusförmigen Wechselspannung geben beide Quellen im Mittel gleiche Leistung ab, wenn der Maximalwert der Leistungsabgabe bei der Wechselspannung (im Beispiel 20 W) gerade das doppelte der zeitlich konstanten Leistung der Gleichspannungsquelle (im Beispiel 10 W) beträgt. Zwischen dem Scheitelwert der Wechselspannung Û (Beispiel Û = 14,14 V) und dem Spannungswert der Gleichspannung Ueff (Beispiel Ueff = 10 V) gilt dann folgender Zusammenhang:
(Beachte: dieser Zusammenhang gilt nur für sinusförmige Wechselspannungen). Man nennt Ueff auch den Effektivwert der
Wechselspannung. |
Hängt der Effektivwert vom Widerstand R des Gerätes ab?
Ändere den Widerstand der Lampen beider Stromkreise auf 5 Ohm.
- Welche Maximalleistung gibt nun die Wechselspannungsquelle ab, welche Leistung die Gleichspannungsquelle?
Wähle als Scheitelwert der Wechselspannungsquelle nun Û = 7,07 V. (Widerstand bleibt bei 5 Ohm)
- Auf welchen Wert muss die Spannung der Gleichspannungsquelle eingestellt werden, damit beide Quellen wieder im zeitlichen Mittel gleiche Leistung abgeben?
Ändere die Frequenz der Wechselspannung.
- Was ändert sich?
- Was ändert sich nicht?
Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:
Sie müssen dazu die gepackte Datei (effektivwert1.zip) herunterladen
und in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder.
Die nötigen Java-Achive sind ebenfalls enthalten.
Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.
| Die Datei herunterladen :
effektivwert1.zip |
Nutzungsbedingungen:
Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern
gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und
Kollegen weitergeben.
Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der
ausdrücklichen Zustimmung.
Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang
Christian und Mario Belloni vom Davidson College, USA (Copyright Hinweise) |