Kondensator im Wechselstromkreis.

Überblick über diese Seite:

• 1) Experiment
• 2) Theorie des Kondensators im Wechselstromkreis.
• 3) Folgerungen aus der Herleitung
• 4) Wechselstromwiderstand des Kondensators
• 5) Das Zeigerdiagramm
• 6) Java-Applet zum Zeigerdiagramm mit Aufgaben.

1.) Experiment.

Ein Kondensator C wird an eine Wechselspannungsquelle angeschlossen. In der Zuleitung liegt noch ein (kleiner) Widerstand. Die Spannung an seinen Anschlüssen ist der Stromstärke in der Zuleitung proportional. Wir oszilloskopieren die Spannung der Quelle und die Stromstärke in der Zuleitung.

Hier ist das Schaltbild des Experimentaufbaus. Als Quelle dient ein Funktionsgenerator oder eine Wechselspannungsquelle (50 Hz). Die Kapazität ist z.B. 4 Mikrofarad. Der Messwiderstand (links vorn im Bild) beträgt 10 Ohm oder weniger. Die Frequenz beträgt bei den Aufnahmen ca. 600 Hz.

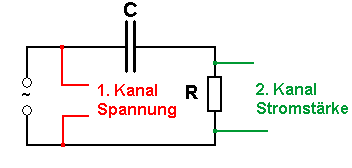
Das zeigt das Oszilloskop:

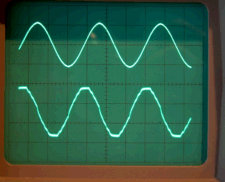In diesem Photo der Oszilloskop-Darstellung ist oben die Spannung und unten die Stromstärke in der Zuleitung (Spannung am Messwiderstand) dargestellt. Oben: Spannung - sinusförmig. Unten: Stromstärke - cosinusförmig.

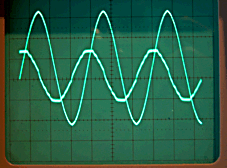Hier sind beide Kurven ineinander verschoben. Man sieht, dass Stromstärke und Spannung nicht gleichzeitig ihren Scheitelwert erreichen. Man sagt, die Kurven haben einen Phasenunterschied. Die Spannung hat einen sinusförmigen Verlauf. (Kurvenverlauf mit der größeren Amplitude) Die Stromstärke (Kurvenverlauf mit kleinerer Amplitude) beginnt ganz links im Oszilloskopbild mit dem Maximalwert. Ihr Verlauf ist also cosinusförmig.

2.) Theorie: Kondensator an einer Wechselspannungsquelle

Die Quelle gibt eine sinusförmige Spannung ab. Für sie gilt:

Dabei ist Û (sprich U-Dach) der Maximalwert oder Scheitelwert der Spannung.
Er entspricht dem, was man in der Akustik die Amplitude einer Tonschwingung nennen würde.

Für die Stärke eines stationären (gleichbleibenden) Stroms gilt:

Ist I(t) zeitabhängig, so gilt für die Momentanstromstärke
(die Definition ist genau parallel z.B. zur Momentangeschwindigkeit bei einer nicht gleichförmigen Bewegung)

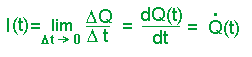
Anschaulich gesprochen bedeutet dies:

Es ergibt sich immer dann eine (Momentan)stromstärke, wenn sich die Ladung auf den Kondensatorplatten verändert. Dann fließt Ladung entweder auf die Kondensatorplatten auf - oder von ihnen herunter.
Die Stromstärke-Zeit-Funktion I(t) ist also die Ableitung der Ladungs-Zeit-Funktion Q(t).

Eine Ableitung nach der Zeit bezeichnen die Physiker mit einem "Punkt" auf der jeweiligen Größe, eine Ableitung nach einer Ortskoordinate wird - wie in der Mathematik - mit einem "Strich" bezeichnet.

Weiter gilt für den Kondensator:

Wenn die Spannung zeitabhängig ist, dann ist es also auch die Ladungsmenge auf den Kondensatorplatten. Die Kapazität C ist eine Konstante.

Wir müssen also Q(t) nach der Zeit ableiten um I(t) zu bekommen (s.o.).
Setzen wir U(t) ein und leiten ab:

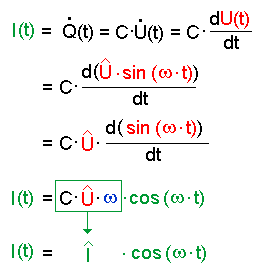
Sinus abgeleitet ergibt cosinus.
Der Faktor Omega im umrahmten Ausdruck stammt aus der inneren Ableitung des Klammerausdrucks.

3.) Folgerungen aus der Herleitung.

Für die Stromstärke gilt also:

• Hat die Spannung einen sinusförmigen Verlauf, so ist der Verlauf der Stromstärke cosinusförmig .
  
  
• Der Scheitelwert der Stromstärke (umrahmter Ausdruck) hängt von verschiedenen Faktoren ab:
  
  
  • Je größer der Scheitelwert der Spannung (Û), desto größer der Scheitelwert der Stromstärke (Î).
    (vgl. Widerstand)
    
    
  • Je größer die Kapazität C, desto größer der Scheitelwert der Stromstärke.
    (Unterschied zum Widerstand, dort wird die Stromstärke kleiner, wenn man den Widerstandswert vergrößert!
    
    
  • Der Scheitelwert der Stromstärke hängt auch von der Frequenz f ab!
    Formal ist dies eine Folge der inneren Ableitung der Sinusfunktion nach der Zeit.
    (je größer die Frequenz, desto größer der Scheitelwert der Stromstärke.
    Beim ohm'schen Widerstand gibt es so eine Abhängigkeit nicht!)

4.) Der Wechselstromwiderstand eines Kondensators.

Lässt man die Phasenlage von Spannung und Stromstärke außer Betracht und konzentriert sich nur auf die Scheitelwerte, so fällt ein ähnlicher Zusammenhang wie beim ohm'schen Gesetz auf:

Je größer die Spannung, desto größer die Stromstärke.
Der Quotient aus Spannung und Stromstärke ist also konstant.

Man definiert daher parallel zur Gleichung R = U/I den sogenannten Wechselstromwiderstand X_C eines Kondensators:

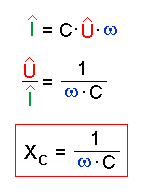Im Gegensatz zum ohm'schen Widerstand ist der Wechselstromwiderstand frequenzabhängig! Erinnerung: w = 2*p*f

5.) Das Zeigerdiagramm.

Ein praktisches Hilfsmittel um sich klar zu machen, wie die Sinus- und Cosinuskurven bei Stromstärke und Spannung zustande kommen, ist das sogenannte Zeigerdiagramm.

Dabei rotiert ein System aus Zeigern gegen den Uhrzeigersinn. Die y-Komponente der jeweiligen Zeigervektoren gibt dann den Momentanwert an.

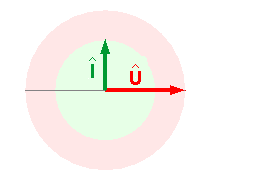Zeitpunkt t = 0 s. Ist die Spannung U(t) sinusförmig, dann ist zur Zeit t = 0 s die Spannung U(t) = 0 V. Der Spannungszeiger deutet horizontal. Die Stromstärke hat dann einen cosinusförmigen Verlauf, d.h. zur Zeit t = 0 s ist die Stromstärke maximal. Der Zeiger für die Stromstärke weist nach oben. Er ist also dem Spannungszeiger um 90 Grad in der Phase voraus. (Dies gilt nicht sofort.)

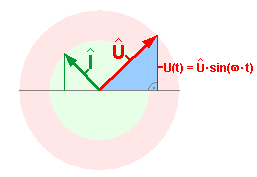Zu einem späteren Zeitpunkt. Man erhält den Momentanwert der beiden Größen zu jedem Zeitpunkt, indem man die vertikale Komponente betrachtet. So entspricht z.B. die Senkrechte rechts im blau eingefärbten Dreieck genau dem Momentanwert der Spannung.

6.) Ein Java-Applet hilft bei der Anschauung - Zeigerdiagramm beim Kondensator.

Arbeite die Punkte in "Aufgaben / Fragen" der Reihenfolge nach durch, sie helfen beim Verständnis der Darstellung.

Aufgaben / Fragen:

1) Phasenlage der Spannungs- und Stromstärkekurve.

Die dünnen vertikalen Linen entsprechen dem Momentanwert der Spannung (rot) und der Stromstärke (grün).
Sie werden rechts im Diagramm in zeitlichen Abfolge aufgetragen.

a) Belasse die voreingestellten Werte und klicke "Schritt >>" mehrmals bis die Zeiger wieder in der Ausgangsstellung stehen.

• Welchen Wert hat die Stromstärke, wenn die Spannung maximal ist?
• Welchen Wert hat die Spannung, wenn die Stromstärke maximal ist?
• Wie müssen also die beiden Vektorzeiger zueinander stehen, um dies richtig darzustellen?

b) Belasse die voreingestellten Werte, klicke aber auf die Option "y-Komponenten zeigen - nein" und klicke "Reset".
Klicke nun "Rotieren".
Beachte, wie sich die die Stromstärke und Spannungskurven aufbauen.

• Welche Kurve erreicht ihren Scheitelwert zeitlich früher (weiter "links") die Spannungskurve oder die Stromstärkekurve?
• Was ist hier anders als bei der idealen Spule im Wechselstromkreis?
  (vgl. hierzu diese Seite)

2.) Scheitelwert der Stromstärke und Wechselstromwiderstand.

c) Verkleinere / vergrößere die Kapazität durch Auswahl im Auswahlfeld "Kapazität". Klicke zunächst wieder "Reset" und dann "Rotieren".

• Wie verändert sich der Scheitelwert der Stromstärke dabei (Länge des grünen Zeigers)?
• Wie ändert sich also der Wechselstromwiderstand des Kondensators?
• Was passiert, wenn man als Kapazität 2000 Mikrofarad nimmt?

d) Belasse nun die Kapazität bei 1000 Mikrofarad. Ändere die Frequenz auf 50 Hz.

• Wie ändert sich dabei die Rotationsgeschwindigkeit der Zeiger?
• Wie ändert sich der Scheitelwert der Stromstärke?
• Wie ändert sich der Wechselstromwiderstand?

Beachte den Unterschied zur Spule im Wechselstromkreis.

Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:

Sie müssen dazu die gepackte Datei (wechs_kond.zip) herunterladen und in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder. Die nötigen Java-Achive sind ebenfalls enthalten.

Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.

Nutzungsbedingungen:

Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und Kollegen weitergeben.

Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der ausdrücklichen Zustimmung.

Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang Christian und Mario Belloni vom Davidson College, USA (Copyright Hinweise)  © Javascript dieses Problems : Klaus-Dieter Grüninger, Landesbildungsserver Baden-Württemberg