Reale Spule im Wechselstromkreis.

Bevor du diese Seite durcharbeitest, solltest du diese beiden Seiten durchgearbeitet und verstanden haben:

• Das Zeigerdiagramm - eine Einführung
• Spule im Wechselstromkreis

Hilfreich ist auch diese Seite:

• Reihenschaltung von Kondensator und Widerstand

1) Das gedankliche Hilfsmittel.

Man betrachtet daher die reale Spule als eine Hintereinanderschaltung einer idealen (widerstandsfreien) Spule und eines ohm'schen Widerstandes. Sein Wert entspricht dem Widerstandswert des Spulendrahtes. Das Schaltbild rechts zeigt dieses "Ersatzverfahren". In der Realität können der Widerstand des Spulendrahtes und die Induktionswirkung eines aufgewickelten Drahtes natürlich nicht voneinandert getrennt werden! Dieses Verfahren ist nur ein gedankliches Hilfsmittel. An den Anschlüssen der Spule misst man also immer die Addition der Teilspannungen von UL und UR. Keine dieser beiden Größen lässt sich bei einer realen Spule getrennt messen.

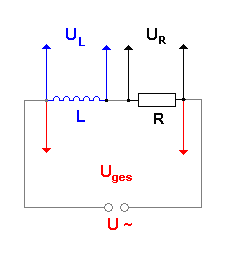2) 3,81 V + 8,54 V = 10,07 V  ??
Im Wechselstromkreis darf man Teilspannungen nicht einfach addieren !

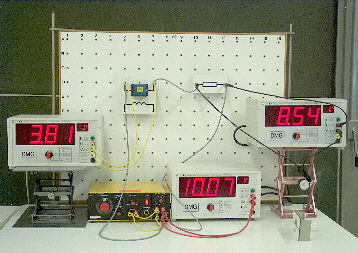Der Versuchsaufbau im Photo entspricht dem Schaltbild von oben. Links sehen wir eine (reale) Spule, deren Widerstand in der weiteren Betrachtung vernachlässigt wird. Die Spannung an der Spule UL beträgt 3,81 V. Der Widerstand des Spulendrahtes wird nun durch den ohm'schen Widerstand rechts repräsentiert. (Der Widerstandswert ist 220 Ohm) Die Spannung am Widerstand UR beträgt 8,54 V. Statt der (vielleicht erwarteten) 12,35 V (3,81V + 8,54V) zeigt das Messinstrument für die Gesamtspannung Uges nur 10,07 V an.

Warum eigentlich nicht??

3) Stromstärke und Teilspannung sind nicht immer phasengleich!

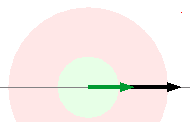	Beim ohm'schen Anteil (Spulenwiderstand) sind Stomstärke (grün) und Spannung ÛR (schwarz)in Phase. Beide Zeiger deuten in der gleichen Richtung.
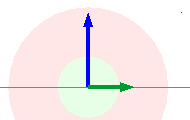	Beim induktiven Anteil (Induktionswirkung der Spule) ist die Stromstärke der Spannung ÛL um 90 Grad in der Phase hinterher (oder die Spannung der Stromstärke um 90 Grad voraus). (vgl. hierzu auch diese Seite)

4) Die Teilspannungen muss man vektoriell addieren.

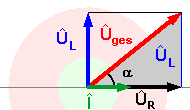Das Zeigersystem soll gegen den Uhrzeigersinn rotieren. Der Vektor für die Stromstärke weist nach rechts. Mit ihm phasengleich ist der Vektor für die Spannung am Widerstand ÛR. Die Spannung an der idealen Spule ÛL ist der Stromstärke in der Phase 90 Grad voraus. Die Gesamtspannung findet man als Vektoraddition von ÛR und ÛL zur Gesamtspannung Ûges (grau unterlegtes, rechtwinkliges Dreieck).

Nach dem Satz des Pythagoras gilt also:

(Û_ges)² = (Û_L)² + (Û_R) ²

5) Auch Wechselstromwiderstände werden vektoriell addiert!

Arbeiten wir mit der Gleichung von oben noch etwas weiter.
Die jeweilige Teilspannung ist das Produkt aus Wechselstromwiderstand und Stromstärke. (vgl. U = R * I)

(Û_ges)² = (Û_L)² + (Û_R) ² = ( X_L * Î )² + ( R * Î )² = (X_L² + R²) * β    (1)

Entsprechend zu U = R * I gilt für den gesamten Wechselstromwiderstand Z der Reihenschaltung von Kondensator und Widerstand:

(Û_ges)² = ( Z * I)²  = Z²* I²   (2)

Ein Vergleich von (1) und (2) ergibt:

Z² * β = (X_L² + R²) * β

oder nach Kürzen von β auf beiden Seiten:

Z² = X_L² + R²

Das bedeutet: auch die Widerstände muss man vektoriell (mit dem Satz des Pythagoras) addieren!
Der gesamte Wechselstrormwiderstand Z ist nicht die Summe der einzelnen Wechselstromwiderstände X_C und R.

6) Der Phasenwinkel zwischen Stromstärke und Gesamtspannung.

Hier ist noch einmal das Zeigerdiagramm. Der Phasenwinkel a zwischen Î und Ûges kann berechnet werden. Im grauen, rechtwinkligen Dreieck gilt: tan a = ÛL / ÛR = (XL * Î) / (R * Î) = XL / R Man kann also den Phasenwinkel sowohl über die Teilspannungen, also auch über die einzelnen Wechselstromwiderstände berechnen. Weil die Spannung der Stromstärke vorauseilt, ist der Phasenwinkel a positiv.

Grenzfälle:

Ist R sehr groß gegenüber X_L, dann ist der Phasenwinkel klein,
ist R sehr klein gegenüber X_L, dann ist der Phasenwinkel groß,
ist R = X_L, dann ist der Phasenwinkel gerade 45 Grad.

7) Das Oszilloskop zeigt, was auch das rotierende Zeigersystem zeigt.

Die Pfeilfarben haben folgende Bedeutung:

• Stromstärke (grün)
• Spannungsanteil ideale Spule (blau)
• Spannungsanteil ohm'scher Widerstand (schwarz)
• Gesamtspannung (rot)

Aufgaben / Fragen:

1) Wähle als Widerstandswert zunächst 0 Ohm. Dann simulieren wir nur die ideale Spule im Wechselstromkreis.
(Zuerst "Reset" und dann "Rotieren" klicken.)

• Wie ist die Phasenlage zwischen Stromstärke I(t) und Spannung U_L(t)?
• Welchen Wert hat die Stromstärke, wenn die Spannung 0 ist?
• Welchen Wert hat die Spannung, wenn die Stromstärke 0 ist?

Nach oben zum Applet

2) Wähle nun den Widerstand wieder mit der Voreinstellung (4 Ohm).
(Beachte auch die Einblendungen der Phase. Die Phase ist der Winkel (in Grad) zwischen dem grünen Vektor der Stromstärke Î und dem roten Vektor der Gesamtspannung Ûges.

a) Wähle zunächst die Darstellungsart "Zeichnen: Spannung Widerstand (UR)".

• Wie ist die Phasenlage zwischen Stromstärke I(t) und U_R(t)?
• Welchen Wert hat U_R(t), wenn I(t) null / maximal ist?

b) Wähle nun die Darstellungsart "Zeichen: Spannung Kondensator (UL)".

• Wie ist die Phasenlage zwischen Stromstärke I(t) und U_L(t)?
• Welchen Wert hat U_L(t), wenn I(t) null / maximal ist?

c) Wähle die Darstellungsart "Zeichen: Gesamtspannung (Uges)".

• Wie ist die Phasenlage zwischen Stromstärke I(t) und U_L(t) jetzt?

Nach oben zum Applet

3) Belasse die Spuleneinstellungen auf der Voreinstellung (1 mH , 50 Hz) und wähle den Widerstand maximal mit 12 Ohm.

• Wie verändern sich die Teilspannungen und der Phasenwinkel dabei?
• Versuche dies zur erklären.

Nach oben zum Applet

4) Wähle nun den Widerstand mit 2 Ohm und verändere die Eigeninduktivität und die Frequenz so, dass die Spannung an der idealen Spule möglichst groß wird.

• Müssen dazu die Frequenz und die Eigeninduktivität groß oder klein gewählt werden?
• Wie verändert sich der Wechselstromwiderstand X_L dabei? (Erinnerung: X_L = w * L)
  
• Was kann man nun über die Phasenlage zwischen Stromstärke und Gesamtspannung aussagen?
  
• Wie groß muss X_L sein, damit der Phasenwinkel genau 45 Grad wird (5 Grad Abweichung)?
  (Versuche dies durch Variation von Eigeninduktivität und Frequenz möglichst genau zu erreichen).
• Berechne mit den ermittelten Werten X_L. Du müsstest eine Wert von etwa 2 Ohm erhalten! (Erinnerung: w = 2*p*f)

Nach oben zum Applet

Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:

Sie müssen dazu die gepackte Datei (wechs_realspule.zip) herunterladen und in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder. Die nötigen Java-Achive sind ebenfalls enthalten.

Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.

Die Datei herunterladen : wechs_realspule.zip

Nutzungsbedingungen:

Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und Kollegen weitergeben.

Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der ausdrücklichen Zustimmung.

Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang Christian und Mario Belloni vom Davidson College, USA (Copyright Hinweise) © Javascript dieses Problems : Klaus-Dieter Grüninger, Landesbildungsserver Baden-Württemberg