Das Zeigerdiagramm - eine Einführung.
Das Zeigerdiagramm ist ein gutes Hilfsmittel um harmonische, periodische Vorgänge - also solche, die sich mit Sinus- und Cosinusfunktionen beschreiben lassen - zu behandeln.
Solche Vorgänge sind in der Physik sehr häuftig, nicht nur in der Wechselstromlehre, sondern auch bei den (mechanischen und elektromagnetischen) Schwingungen und Wellen.
Auch die Wechselspannung in unserem Stromnetz hat einen solchen Verlauf, d.h. sie wechselt nicht nur ständig die Polung, sondern auch den Betrag der Spannung.
Der "Einheitskreis".
Man benutzt zunächst eine Art "Einheitskreis" (rosa
eingefärbter Kreis in der Simulation), auf dem ein Zeiger rotieren kann.
Der Radius dieses "Einheitskreises" entspricht der
Amplitude oder dem Scheitelwert einer
Schwingung.
Bei der sinusförmigen Wechselspannung spricht man von der
Scheitelspannung Û.
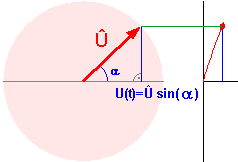 |
Dieses Bild zeigt eine Momentaufnahme aus der Simulation weiter unten auf
dieser Seite: Der Sinus des Winkels a ist die Gegenkathete / Hypothenuse. Damit ist die blaue Strecke also: U = Û * sin(a). |
Eine Parallele wird benutzt.
Dreht sich der Pfeil auf der Scheibe, dann ändert sich auch der Winkel
a ständig.
Rotiert die Scheibe mit konstanter Drehfrequenz, wird in doppelter
Zeit auch der doppelte Winkel überstrichen, in dreifacher
Zeit der dreifache Winkel.
Dies ist parallel zur (linearen) gleichförmigen Bewegung.
Dort wird in doppelter Zeit die doppelte Strecke bzw. in dreifacher Zeit
dreifache Strecke zurückgelegt.
Die folgende Gegenüberstellung verdeutlicht diese Parallele:

Je größer die Geschwindigkeit / Winkelgeschwindigkeit desto größer ist die in einem Zeitintervall zurückgelegte Stecke / der überstrichene Winkel.
Dabei gilt für die Winkelgeschwindigkeit, die Drehfrequenz f und die Umlaufdauer T folgender Zusammenhang:
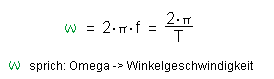
Vom rotierenden Zeiger zur Sinuslinie.
Der y-Achsenabschnitt U(t) = Û *
sin(w*t) wird nach rechts ins Diagramm
übertragen
(beachte die grüne Hilfslinie) und die Werte zeitlich nacheinander
aufgetragen.
Fragen / Aufgaben:
Belasse zunächst die Grundeinstellungen und die Frequenz bei 50 Hz.
Klicke "Rotieren" oder "Schritt >>".
- Welche Zeit vergeht bis der Zeiger senkrecht steht?
- Unter welchem Winkel steht der Zeiger, wenn man gerade die Hälfte dieser Zeit vergangen ist?
- Wie lange dauert eine halbe / eine ganze Umdrehung?
- Wie groß ist also die Periodendauer T der Sinusschwingung?
- Prüfe dieses Ergebnis mit der eingestellten Frequenz f nach. (Erinnerung T = 1/f)
Ändere nun die Frequenz. Wähle z.B. 25 Hz und auch 100 Hz.
- Wie ändern sich dabei die Umdrehungsdauer der Scheibe bzw. die Periodendauer T der Wechselspannung?
Anfangsbedingungen - auf den Startpunkt kommt es an!
Man kann die Simulation auch so abändern, dass zum Zeitpunkt t = 0 s die Spannung mit dem positiven Maximalwert beginnt.
Wähle dazu "Phase 90 Grad" und klicke "Reset", der Zeiger wird dabei um 90 Grad "weitergedreht", bevor gestartet wird
Denke an folgende mathematische Zuordnungen:
| sin(a + 90°) = cos(a) |
| sin(a + 180°) = -sin(a) |
| sin(a + 270°) = -cos(a) |
- Welche Funktion hat man auf diese Art aus der Sinusfunktion gemacht?
- Welchen Wert nimmt cos(w*t) zum Zeitpunkt t = 0 s an?
- Welchen Wert hat damit die Spannung ganz zu Beginn der Simulation?
(Prüfe in der Simulation nach!)
Probiere auch die anderen Einstellungen des Phasenwinkels aus.
- Versuche jeweils die richtige Funktion anzugeben.
Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:
Sie müssen dazu die gepackte Datei (zeigerdiagramm.zip) herunterladen
und in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder.
Die nötigen Java-Achive sind ebenfalls enthalten.
Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.
| Die Datei herunterladen :
zeigerdiagramm.zip |
Nutzungsbedingungen:
Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern
gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und
Kollegen weitergeben.
Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der
ausdrücklichen Zustimmung.
Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang
Christian und Mario Belloni vom Davidson College, USA (Copyright Hinweise) |


