Entropie.

3.) Entropietransport: wozu man beim Kraftwerk den Kühlturm braucht.

• Sieh dir den nächsten Abschnitt aus dem Vortrag von Martin Buchholz an.
• Lies anschließend wieder unten die Zusammenfassung durch.

3.1.) Der Weg der Energie (rot).

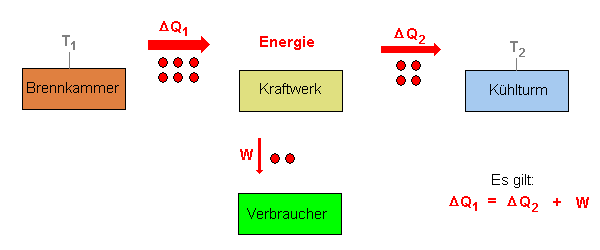
In der Brennkammer wird die Wärmemenge ΔQ₁ erzeugt. Ein Teil dieser Wärmemenge wird im Kraftwerk (eigentlich im Generator) in elektrische Energie W umgewandelt und geht zum Kunden (Verbraucher). Ein anderer Teil der zugeführten Wärmemenge geht als Abwärme ΔQ₂ an den Kühlturm.

Es gilt der 1. Hauptsatz der Wärmelehre: ΔQ₁ = ΔQ₂ + W

Je dicker der Pfeil in der Darstellung, um so mehr Energie nimmt diesen Weg. Die roten Kugeln stehen wie im Vortrag für Energie oder Wärmeportionen.

3.2.) Der Weg der Entropie (blau).

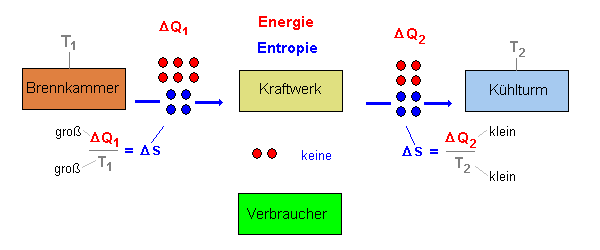
Zusammen mit Wärme wird immer auch Entropie übertragen. Mechanische oder elektrische Energie überträgt keine Entropie.
Im idealen Kraftwerk ist die Entropiemenge, die von der Brennkammer ins Kraftwerk kommt, gleich groß wie die Entropiemenge, die vom Kraftwerk zum Kühlturm geht (4 blaue Kugeln entsprechen vier Portionen Entropie).

Wie kann das sein, wo doch die Wärmemengen ΔQ₁ und ΔQ₂ nicht gleich sind?

Für die Entropieübertragung spielt auch die (absolute) Temperatur T, bei der sie erfolgt, eine Rolle:
die Wärmemenge ΔQ₁ ist zwar groß, aber die Temperatur T₁ bei der die Entropie ins Kraftwerk übertragen wird, ist es auch.
Dafür verlässt nur die kleinere Wärmemenge ΔQ₂ das Kraftwerk, aber auch bei kleiner Temperatur T₂.
Das gleicht sich aus (vgl. Skizze). So wird die ganze Entropie wieder abgegeben.

3.3.) Exkurs: Wie effektiv kann ein ideales Kraftwerk maximal sein?

Da ein Teil der zugeführten Wärmemenge ΔQ₁ immer als "Abwärme" an den Kühlturm geht, kann niemals die gesamte Wärmemenge ΔQ₁ in elektrische Energie gewandelt werden.

Die Abwärme ist uns egal, wir hätten gerne möglichst viel elektrische Energie aus der zugeführten Wärmemenge gewonnen. In diesem Zusammenhang ist der Begriff des Wirkungsgrads η wichtig. Er sollte möglichst hoch sein.

Im gezeichneten Beispiel von oben ist die zugeführte Wärmemenge 6 Energieportionen, in elektrische Energie werden gewandelt 2 Energieportionen. Der Wirkungsgrad ist also 2 / 6 = 1 / 3 = 0,333 = 33%.

Wie groß kann der Wirkungsgrad eines idealen Kraftwerks werden und wovon hängt das ab?

Beim idealen Kraftwerk ist, wie oben erklärt, die zugeführte Entropie gleich der abgeführten Entropie.
Es ergibt sich also:

Mit anderen Worten der Wirkungsgrad ist 1 (100%) minus dem Quotienten aus der Abwärme ΔQ₂ und der zugeführten Wärmemenge ΔQ₁. Je kleiner die Abwärmemenge ΔQ₂ desto besser ist der Wirkungsgrad - das hatten wir uns ja schon gedacht.....

Wie hängt der Wirkungsgrad aber von den Temperaturen der Brennkammer T₁ und des Kühlturms T₂ ab?

Dazu setzen wir die Gleichung (1) von oben für ΔQ₂ ein:

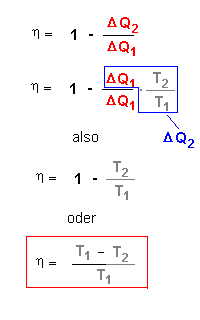
Damit können wir jetzt eine Abschätzung machen.
Die Temperatur der Brennkammer hängt natürlich davon ab, was wir dort verbrennen, ob z.B. Steinkohle oder Braunkohle und auch davon welchen Wassergehalt die Kohle hat. Auch die Menge, die Feuchtigkeit und die Temperatur der zugeführten Verbrennungsluft spielt eine Rolle.
Nimm für die Temperatur der Brennkammer 800°C an und für die Temperatur des Kühlturms 20°C.

Welchen maximalen Wirkungsgrad kann das Kraftwerk haben?

Daran denken, es geht um absolute Temperaturen - 0°C = 273 K! Also ist T₁ 1073 K und T₂ 293 K. Als Wirkungsgrad ergibt sich dann 72,6%. Besser geht es prinzipiell nicht!

Diese Überlegung (Carnot-Prozess) gilt im Prinzip für jede Art Wärmekraftmaschine (ein Kraftwerk ist nichts anderes), also auch z.B. für einen Automotor.

Schätze seinen maximalen Wirkungsgrad ab, wenn er zwischen 250°C (Motorblock) und 20°C (Auspuff hinten) arbeitet.

Es geht nicht besser, aber es geht schlechter! - Nächste Seite / Filmausschnitt: reales Kraftwerk - zweiter Hauptsatz der Wärmelehre