Entropie.
5.) Reversible und irreversible Vorgänge, Dissipation.
- Sieh dir den nächsten Abschnitt aus dem Vortrag von Martin Buchholz an.
- Lies anschließend wieder unten die Zusammenfassung durch.
5.1.) Reversible Vorgänge.
Geht in ein System gleich viel Entropie hinein wie hinausgeht, dann laufen in
dem System nur Vorgänge ab, bei denen keine Entropie
entsteht, es handelt es sich dann um einen reversiblen Vorgang.
"Reversibel" bedeutet "umkehrbar", d.h.
die Vorgänge können in beiden Richtungen ablaufen.
In diesem Fall wird der Umgebung mit niedrigerer Temperatur
("Kühlturm") Wärmeenergie entzogen. Der Generator
läuft dann als Motor und der Umgebung mit höherer Temperatur
("Brennkammer") wird Energie zugeführt. Von der kühleren
Umgebung strömt so viel Entropie in die Wärmekraftmaschine, wie auch
in die Umgebung mit höherer Temperatur wieder abfließt.
Es bleibt keine Entropie in dem System.
Bei einem Kraftwerk macht so etwas natürlich wenig Sinn, man benutzt das Prinzip aber bei einer (idealen) Wärmepumpe oder bei einem Kühl- oder Gefrierschrank (vgl. dazu die Grafiken).
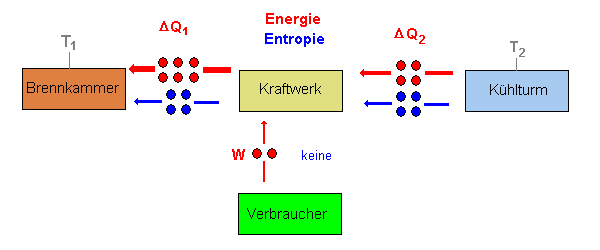
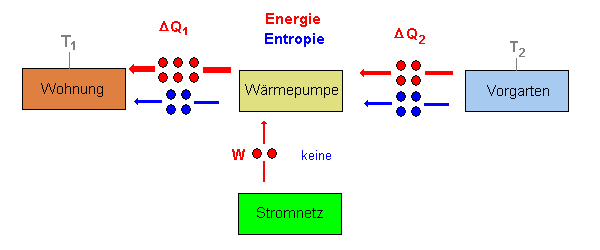
- Welche Teile beim Kraftwerk und bei der Wärmepumpe entsprechen
sich?
- Was entspricht der "Wohnung" und dem "Vorgarten" beim Kühl- und Gefrierschrank?
5.2.) Irreversible Vorgänge.
Die meisten Vorgänge sind aber "irreversibel", d.h.
"nicht umkehrbar", sie können also nur in einer
Richtung ablaufen.
Warum?
Auf dieser Seite zum realen Kraftwerk haben wir gelernt, dass dort
- weniger Energie umgewandelt wird als beim idealen Kraftwerk, es also einen kleineren Wirkungsgrad hat,
- also mehr Abwärme entsteht
- daher mehr Entropie abgeführt wird als zugeführt wird, also im System Entropie entsteht.
Betrachtet man das reale Kraftwerk umgekehrt, so würden vom
Kühlturm rechts 5 Entropieportionen ("blaue Kugeln") in das
Kraftwerk einströmen, aber nur 4 Entropieportionen würden das
Kraftwerk nach links wieder verlassen. Dann müsste im Kraftwerk
Entropie vernichtet werden und das gibt es
nicht!
Nach dem zweiten Hauptsatz kann die Entropie nur größer werden
(ΔS > 0) oder gleich bleiben (ΔS = 0).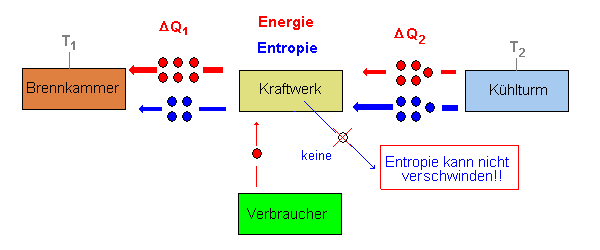
Der Vorgang kann in dieser Richtung also nicht funktionieren, er ist
irreversibel!
Was von der Energiebilanz (1.Hauptsatz) her möglich wäre, verbietet
die Entropiebilanz (2.Hauptsatz).
5.3.) Dissipation.
Wenn wir beim Auto bremsen, dann werden die Bremsscheiben erwärmt.
Durch Abkühlen der Bremsscheibe kann man das Autos leider nicht wieder
beschleunigen - der Vorgang ist irreversibel!
Die wertvolle kinetische Energie des Autos ist für immer verloren - sie
ist entwertet, quasi "verschwendet".
Daher spricht man bei solchen Vorgängen von
Dissipation (lat.
dissipare = verschwenden, zerstreuen).
Sie verschwindet in die Umgebung, denn das Auto ist kein
abgeschlossenes System.
Martin Buchholz stellt in seinem Film Beispiele irreversibler
Vorgänge aus dem Alltag vor.
Sicher fallen dir zahlreiche weitere Beispiele ein.
Die Suche nach reversiblen Vorgängen wird dir schon deutlich
schwerer fallen!
Ist das Fadenpendel wirklich ein reversibler Vorgang, wie (vereinfachend) im Film behauptet?
Lage- und Bewegungsenergie werden auch bei diesem System nicht
vollständig ineinander umgewandelt, ein Teil wird auch in Form von
Wärme an die Umgebung "verschwendet". Das System Fadenpendel
produziert also laufend Entropie. Die Amplitude nimmt ab, irgendwann kommt das
Pendel zur Ruhe. Die anfängliche Lageenergie ist dann komplett
verloren.
Betrachtet man nur eine oder zwei Schwingungen, so ist dieser Effekt bei einem
gut aufgehängten Pendel natürlich sehr klein und kann (wie im
Vortrag) vernachlässigt werden.
5.4.) Dissipation beim elektrischen Schwingkreis.
Jedes schwingende System zeigt also Dissipation und Entropieerzeugung,
dies gilt vor allem auch für das Feder-Masse-Pendel und den
elektrischen Schwingkreis. |
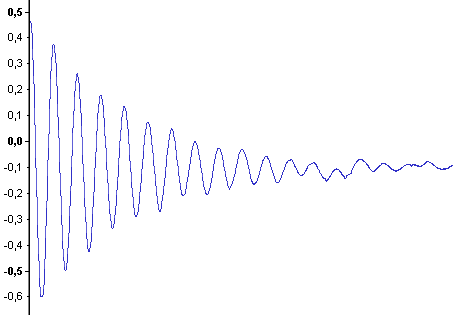 |
Wie kommt dieser (exponentielle) Abfall der Spannung zustande?
Betrachten wir dazu das folgende Diagramm.
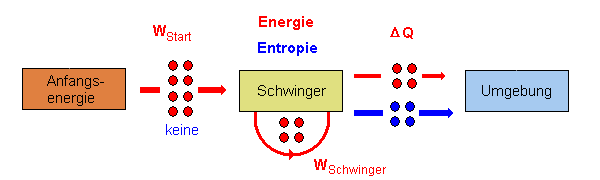
Zu
Beginn wird der Kondensator geladen. Die Anfangsenergie (8 Energieportionen)
werden in das System gesteckt. Nehmen wir an, dass das System so stark
gedämpft sei, dass nach einer Schwingung nur noch die Hälfte
der Energie im schwingenden System ist (4 Energieportionen), die andere
Hälfte wurde an die Umgebung abgegeben - zusammen mit Entropie (vgl.
Skizze).
Am Ende der nächsten Schwingung ist wieder die Hälfte an Energie
entwertet, d.h. es sind noch 2 Energieportionen im System und 2 wurden an die
Umgebung abgegeben. Nach drei Perioden ist noch 1 Energieportion im System und
eine wurde abgegeben.
Du hast sicher gemerkt, dass dies dieselbe Gesetzmäßigkeit wie beim radioaktiven Zerfall oder bei der Entladung eines Kondensators über einen Widerstand ist. Eine Periode T wäre hier also auch genau die Halbwertszeit der Amplitudenabnahme.
Ein solcher Zusammenhang ergibt sich gerade bei der Kombination eines
Kondensators von 4 Mikrofarad und einer Phywe 35 mH Spule (1200 Wdg). |
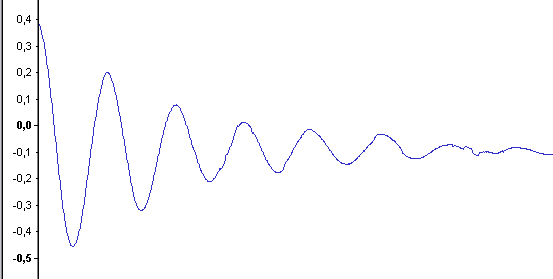 |
Mathematisch stellt man dann den Zusammenhang folgendermaßen dar:
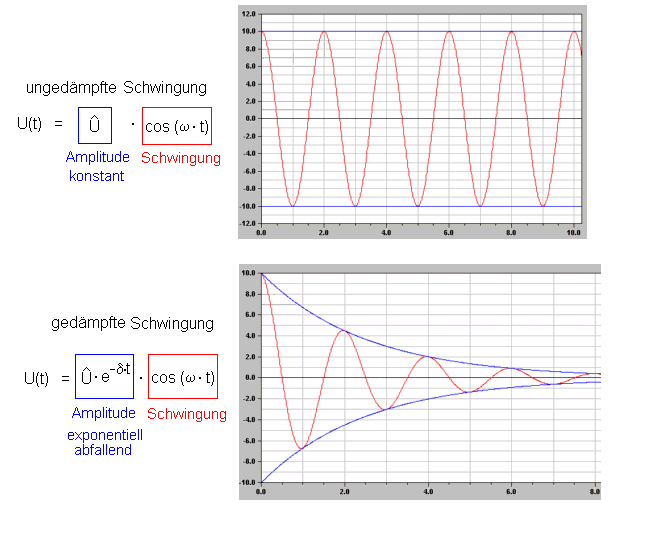 |
Bei der ungedämpften Schwingung bleibt die Amplitude U-Dach konstant,
bei der gedämpften Schwingung nimmt sie exponentiell ab (blauer
Formelanteil und blaue Hüllkurve). Der Faktor δ heißt Dämpfungsfaktor oder Dämpfungskonstante. Ist δ = 0 so wird e-0 also 1 - es ergibt sich dann die ungedämpfte Schwingung. Je größer δ desto stärker gedämpft ist die Schwingung, d.h. um so größer ist der ohmsche Widerstand des Spulendrahts im Schwingkreis. Es kann sogar passieren, dass die Dämpfung so stark ist, dass die Amplitude schon während der ersten Schwingung praktisch auf 0 abnimmt. Dies nennt man den aperiodischen Grenzfall. |
5.5.) Weitere Materialien zum Thema - Modellbildung.
Eine Modellbildung zum analogen mechanischen Problem Feder-Schwere-Pendel mit Hilfe des Modellbildungssystems PAKMA findet man auf dieser Seite der Lehrerfortbildung Baden-Württemberg. Natürlich lässt sich der Alogithmus auch mit jedem anderen Modellbildungssystem entsprechend verwirklichen.


