Umrechnung von Geschwindigkeiten.
Umrechnung von m/s in km/h und umgekehrt.
1.) Einheiten der Geschwindigkeit.

|
Was will uns das runde Schild mit dem roten Rand sagen? Auf modernen Schildern zur Geschwindigkeitsbeschränkung ist heute gar keine Einheit mehr angegeben (vgl. unteres Schild). Dieses Schild bedeutet, dass man sich hier in einer "Tempo-30-Zone" befindet, in der nur maximal 30 km/h schnell gefahren werden darf. |
 |
Neben der Einheit km/h (Kilometer pro Stunde) gibt es auch noch
zahlreiche andere Geschwindigkeitseinheiten: sehr gebräuchlich ist noch
m/s (Meter pro Sekunde). |
Auf alle Fälle gilt aber: Geschwindigkeit v = zurückgelegte Wegstrecke δs / dafür nötige Zeit δt. |
2.) Umrechnung von Geschwindigkeitseinheiten.
In der Physik brauchen wir häufiger die Umrechnung zwischen den
Einheiten km/h und m/s.
Das ist leider nicht ganz so einfach, denn die Zeit passt nicht ins
Hunderter- oder Tausendersystem.
Eine Minute hat bekanntlich 60 s und eine Stunde hat 60 Minuten - also 3600
Sekunden (60*60).
Wir wollen die Umrechnungen hier einmal kurz vorführen:
2.1.) Umrechnung km/h in m/s.
So ausführlich musst du das natürlich nicht immer machen. Wir gehen hier bewusst viele kleine Schritte, um es besonders klar zu machen. Zahlen und Einheiten der Wegstrecken sind in rot, Zahlen und Einheiten der Zeit in blau wiedergegeben. Beim letzten Schritt rechts wird Zähler und Nenner jeweils durch 1000 geteilt.
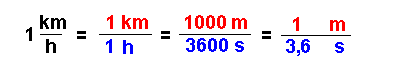
| Bei Umrechnung von km/h in m/s muss man den Zahlenwert durch 3,6 teilen. |
Häufige Geschwindigkeitsumrechnungen in Aufgaben:
|
Diese im Straßenverkehr üblichen Geschwindigkeiten, kommen in
Aufgaben öfter vor (gerundet auf zwei Nachkommastellen). |
2.2.) Umrechnung m/s in km/h.
Hier nun die umgekehrte Umrechnung. Diese ist etwas schwieriger. Dazu musst
du wissen, dass dann 1 m = 1/1000 km ist und 1 s = 1/3600
h.
Dann wird bekanntlich durch einen Bruch dividiert, indem man mit dem Kehrwert
multipliziert! Also:

| Bei Umrechnung von m/s in km/h muss man den Zahlenwert mit 3,6 multiplizieren. |
Häufige Geschwindigkeitsumrechnungen in Aufgaben:
|
Tipp: Hier sind ein paar Zahlenwerte, die man öfter braucht und von denen man sich wenigstens einen merken sollte. Am besten ist die erste oder dritte Zeile: Wenn du zu Fuß unterwegs bist, dann machst du in jeder Sekunde etwa einen Schritt. Ist deine Schrittweite 1 m, dann bis du also mit der Geschwindigkeit 1 m/s unterwegs. Das sind in einer Stunde 3600 Schritte, also 3600 m = 3,6 km. Deine Geschwindigkeit ist also 3,6 km/h. Ein guter 100-m Läufer schafft diese Strecke in etwa 10 Sekunden. Seine (Durchschnitts-)geschwindigkeit ist damit 10 m/s, das sind 36 km/h. |
3.) Probleme und Tipps für die Praxis.
3.1.) Multiplizieren oder dividieren - das ist hier die Frage.
Tipp: Meist erinnern sich Schülerinnen und
Schüler noch daran, dass man bei der Umrechnung einen Faktor 3,6 braucht.
Aber wie war das noch einmal, muss ich jetzt mit 3,6 malnehmen oder
durch 3,6 teilen?
Versuche es mit dem "gesunden Menschenverstand" und deiner
Alltagserfahrung:
Was sind 18 km/h in m/s?
18 km/h, das ist etwa die Geschwindigkeit, mit der ich mit dem Fahrrad
unterwegs bin.
Sind das jetzt 5 m/s (18 / 3,6) oder 64,8 m/s (18 * 3,6)?
Wie weit komme ich dann in einer Sekunde - 5 m oder 64,8 m?
5 m ist etwa die Länge eines Autos, 64,8 m ist etwas mehr als die
Entfernung zwischen zwei Straßenbegrenzungsprosten. Das kann also nicht
sein, so schnell bist du nicht!!
Damit ist die Lösung klar.
| Du kannst dir aber auch folgenden Tipp merken: "Die größere Zahl gehört zur größeren Einheit (km/h)." |
3.2.) Das Problem mit der Darstellung.
Was auch immer wieder falsch gemacht wird, ist folgende Darstellung:
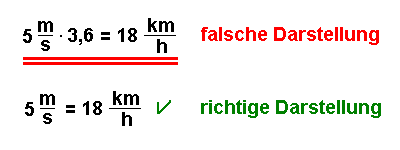
Warum ist die obere Darstellung falsch?
Nun, wenn du die Zahlen links multiplizierst, dann steht links und rechts vom
Gleichheitszeichen die Zahl 18 (denn 5 * 3,6 sind 18).
Nun behauptet die Gleichung aber, dass 18 m/s das Gleiche ist wie 18 km/h - und
das stimmt natürlich nicht!
Die untere Darstellung ist so wie es sein soll. Der Faktor 3,6 wird nur gedacht
und gerechnet, aber nicht geschrieben!


