Zwei beschleunigte Bewegungen -
freier Fall und schiefe Ebene im Vergleich.

Der freie Fall und die schiefe Ebene sind wichtige Anwendungen einer (gleichmäßig) beschleunigten Bewegung.
Zwischen beiden Bewegungen gibt es viele Gemeinsamkeiten, aber auch Unterschiede.
Reibung und Luftwiderstand werden hier nicht berücksichtigt.

	Freier Fall	Schiefe Ebene
beschleunigende Kraft	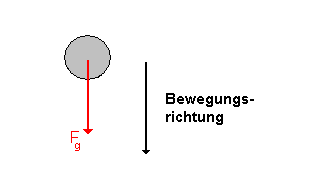Als beschleunigende Kraft wirkt die Schwerkraft Fg. (Man nennt sie auch Gewichtskraft oder Gravitationskraft.)	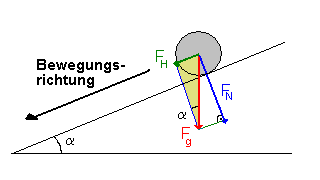Die beschleunigende Kraft, welche die Kugel "den Hang hinunter treibt", ist die Hangabtriebskraft FH. Sie ist eine Teilkraft (Komponente) der Schwerkraft Fg. Zwischen Hangabtriebskraft und Schwerkraft gilt folgender Zusammenhang: FH = Fg * sin α (vgl. gelb hinterlegtes Dreieck). vgl. Seiten zur Kräfteaddition und Kräftezerlegung.
Abhängigkeit der Kraft	Die beschleunigende Kraft Fg ist immer dieselbe, sie hängt von keiner anderen Größe ab (mehr vgl. unten unter "Gemeinsamkeiten").	Die beschleunigende Kraft hängt vom Hangwinkel α ab: steiler Hang -> großer Winkel α-> FH groß flacher Hang -> kleiner Winkel α-> FH klein. Extremfälle: α = 0° -> sin α = 0 -> FH = 0 d.h. es wirkt keine Kraft (Ebene) α = 90° -> sin α = 1 -> FH = Fg -> freier Fall (vgl. linke Tabellenspalte).
Kraft, Masse, Beschleunigung	Es gilt: Fg = m * g Nach dem zweiten Gesetz von Newton ist die Beschleunigung zur einwirkenden Kraft proportional. Es gilt: F = m * a Für die Beschleunigung folgt also: 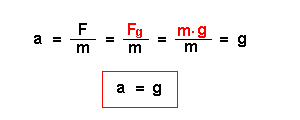Bei freien Fall wirkt auf alle Körper - unabhängig von ihrer Masse - dieselbe Beschleunigung g.	Es gilt: FH = m * g * sin α Nach dem zweiten Gesetz von Newton ist die Beschleunigung zur einwirkenden Kraft proportional. Es gilt: F = m * a Für die Beschleunigung folgt also: 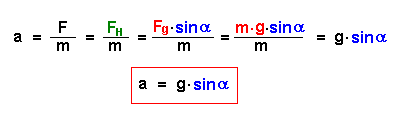Bei der schiefen Ebene wirkt auf alle Körper - unabhängig von ihrer Masse - dieselbe Beschleunigung a.
Bewegungsgleichungen:	Weg-Zeit-Gesetz: s = 1/2 * g * t2 Geschwindigkeits-Zeit-Gesetz: v = g * t	Weg-Zeit-Gesetz: s = 1/2 * a * t2 Geschwindigkeits-Zeit-Gesetz: v = a * t wobei a = g * sin α ist.

Verdeutlichung zur Herleitung der Beschleunigung.

Die Masse von Körpern zeigt sich auf zwei Arten:

• Körper sind schwer, sie haben eine schwere Masse m_s.
  Je größer die Masse eines Körpers ist, desto größer ist auch die Schwerkraft F_g mit der die Erde ihn anzieht.
  Wir müssen also auch eine größere Kraft aufwenden um ihn anzuheben.
  
  Diese Eigenschaft wird mit der Gleichung F_g = m_s * g beschrieben.
  
  
• Körper sind träge, sie haben eine träge Masse m_t.
  Je größer die Masse eines Körpers ist, desto schwerer fällt es uns ihn in Bewegung zu versetzen.
  Ein Kind auf einem Bobbycar anzuschieben erfordert weniger Kraft als ein Auto anzuschieben.
  
  Diese Eigenschaft wird mit der Gleichung F = m_t * a beschrieben.

Meist unterscheidet man nicht zwischen schwerer und träger Masse, sondern setzt diese beiden Eigenschaften gewissermaßen gleich und spricht einfach von der Masse m. So ist es auch in der Herleitung oben gemacht.

Gemeinsamkeiten:

In beiden Fällen

• ergibt sich eine konstante Beschleunigung,
  
  
• hängt die Beschleunigung nicht von der Masse des beschleunigten Körpers ab,
  
  
• spielt der Ort, an dem die Beschleunigung erfolgt, eine Rolle:
  Auf dem Mond z.B. ist g kleiner, d.h. fallende Körper werden dort weniger stark beschleunigt.
  Dasselbe gilt auch für die Beschleunigung auf einer schiefen Ebene auf dem Mond.

Unterschiede:

• Beim freien Fall ist die Beschleunigung an einem festen Ort für alle Körper gleich.
  Die Beschleunigung a hängt von nichts anderem mehr ab, sie ist immer die Fallbeschleunigung g.
  
  
• Bei der schiefen Ebene ist die Beschleunigung ebenfalls für alle Körper gleich groß.
  Die Beschleunigung a hängt hier aber noch vom Hangwinkel α ab, sie ist g * sin α.
  
  
• Für einen Hangwinkel von α = 90° geht die Bewegung auf der schiefen Ebene in den freien Fall über.
  Anders gesagt: der freie Fall ist der Sonderfall der Bewegung auf einer schiefen Ebene - für einen Hangwinkel von 90°.

Eine ähnliche Analogie ergibt sich für den senkrechten Wurf nach oben (1. Teil) und die Bewegung einer Kugel, die eine schiefe Ebene nach oben rollt.
Eine entsprechende Tabelle wirst du sicher leicht erstellen können. Ein Formular dazu gibt es hier:

Du kanst deine Lösung auf der Seite: Zwei Bremsbewegungen - senkrechter Wurf und schiefe Ebene im Vergleich überprüfen
Zwei Bremsbewegungen -
senkrechter Wurf und schiefe Ebene im Vergleich.

Grüninger, Landesbildungsserver, 2015