Kräfte an der schiefen Ebene.

1) Die Schwerkraft wirkt hier anders - Zerlegung in Teilkräfte.

Auf jeden Körper übt die Erde eine Schwerkraft F_g aus. Diese ist um so größer, je größer die Masse m des Körpers ist.

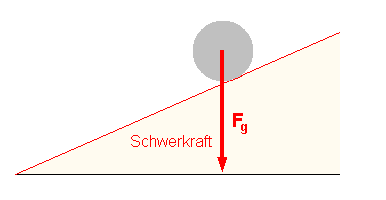
Befindet sich z.B. eine Kugel auf einer schiefen Ebene, so wirkt die Schwerkraft in eine Richtung, in die sich die Kugel nicht bewegen kann. Was wird die Kugel also tun?

Die Schwerkraft muss in zwei Teilkräfte (Komponenten) zerlegt werden, denn es passieren nun zwei Dinge: die Kugel wird den Hang hinunterrollen. Eine Teilkraft wirkt also den Hang abwärts - man nennt sie die Hangabtriebskraft FH. die Kugel drückt nach wie vor (senkrecht) auf die Unterlage. Man nennt diese Teilkraft die Normalkraft FN (normal = senkrecht auf).

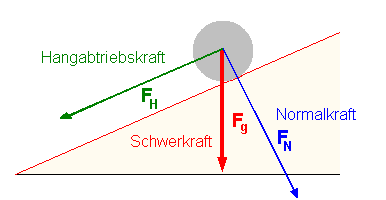2) Auf der Suche nach den Beträgen der Teilkräfte.

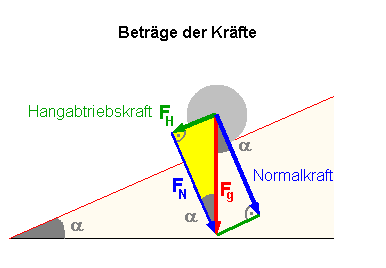
Damit sind die Richtungen der Teilkräfte klar. Nun muss man noch ihre Beträge ermitteln. Man tut dies, indem man zu einem Parallelogramm ergänzt, so dass die Diagonale die Schwerkraft Fg ist. (Weil Hangabtriebskraft FH (parallel zum Hang) und Normalkraft FN (senkrecht zum Hang) immer senkrecht aufeinanderstehen, gibt es in diesem Fall immer ein Rechteck, das aus zwei rechtwinkligen Dreiecken besteht - vgl. Skizze rechts) Der Neigungswinkel α des Hanges kommt im gelb hinterlegten Kräftedreieck auch vor. Die Hypotenuse (längste Seite dieses Dreiecks) ist die Schwerkraft Fg (rot). Die Gegenkathete (dem Winkel α gegenüber) ist die Hangabtriebskraft FH (grün). Die Ankathete (am Winkel) ist die Normalkraft FN (blau).

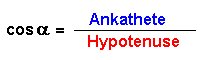
Es gelten folgende trigonometrische Beziehungen:

Trigonometrie	auf das Dreieck angewendet	nach der Teilkomponente aufgelöst

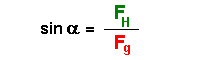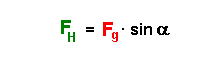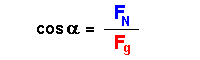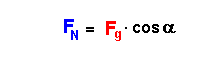3. Grenzfälle.

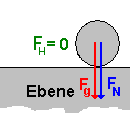
Winkel 0° Der Sinus bei 0° Winkel ist 0. Also ist die Hangabtriebskraft ebenfalls 0 - das ist auch logisch, denn bei 0° sind wir in der Ebene, da gibt es keine Hangabtriebskraft! Der Cosinus bei 0° Winkel ist 1. Die Normalkraft FN ist dann genau die Schwerkraft Fg, d.h. die Kugel drückt mit ganzer Schwerkraft auf die Unterlage.
Winkel 90° Der Sinus bei 90° Winkel ist 1. Bei 90° fällt die Kugel sozusagen frei am Hang entlang ohne ihn zu berühren. Dann wird die Hangabtriebskraft FH gleich der Schwerkraft Fg - es ergibt sich der freie Fall. Der Cosinus bei 90° Winkel ist 0. Die Normalkraft FN ist dann 0, die Kugel drückt nicht mehr auf die Unterlage.

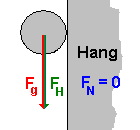4. Die Beschleunigung / Verzögerung.

Die Bewegung der Kugel den Hang hinunter ist eine gleichmäßig beschleunigte Bewegung. Die Beschleunigung a ist also konstant.
Warum?

Nach dem zweiten Gesetz von Newton gilt:

Die beschleunigende Kraft ist die Hangabtriebskraft F_H, wir setzen ein, drücken F_H mit Schwerkraft F_g und Winkel aus (s.o.) und vereinfachen.

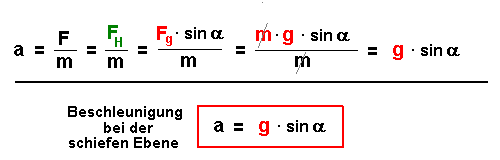
4.1.) Die Beschleunigung hängt vom Hangwinkel ab: konstante Neigung - konstante Beschleunigung.

Bei einem steilen Hang (großes α), ist also auch die Beschleunigung a groß.

Hat der Hang eine konstante Neigung (α konstant), so ist auch die Beschleunigung a überall gleich groß - es ergibt sich eine gleichmäßig beschleunigte Bewegung, wenn sich die Kugel den Hang hinunterbewegt.

Bewegt sie sich den Hang hinauf, so wirkt die Hangabtriebskraft als Bremskraft, denn sie wirkt der Bewegung entgegen.
Es ergibt sich dann eine Bremsbewegung mit konstanter Verzögerung a (negativer Beschleunigung), die ebenfalls g * sinα ist.

4.2.) Die Beschleunigung hängt nicht von der Masse ab.

Da man nicht zwischen schwerer und träger Masse unterscheidet, kürzt sich die Masse heraus: das bedeutet, dass die Masse für die Beschleunigung / Verzögerung am Hang gar keine Rolle spielt!
Sieht man von der Reibung ab, so kommen alle Körper, egal ob groß oder klein, leicht oder schwer, gleichzeitig unten an!
Die Überlegung ist parallel zur Fallbeschleunigung g beim freien Fall.

Mehr zu diesem Vergleich schiefe Ebene und freier Fall findest du hier: Vergleich: freier Fall und schiefe Ebene

Das folgende Java-Applet zeigt die Bewegung einer Kugel auf einer schiefen Ebene. Von der Reibung wird abgesehen.