Energieerhaltung beim senkrechten Wurf.
1) Die Symmetrie der Bewegung.
Berechnet man die Höhen einer Kugel über dem Boden bei einer
Abwurfgeschwindigkeit von vo = 5 m/s, so ergibt sich die
folgende Tabelle.
Mehr dazu auf dieser Seite
Symmetrie beim senkrechten
Wurf.
| Bewegungsanteil | Zeit t | gleichförmiger Anteil s1 = vo * t |
Fallanteil s2 = -1/2 * g * t2 |
Gesamtstrecke sges = s1 + s2 |
Geschwindigkeit v = vo - g * t |
| Steigbewegung | 0 s | 0 m | 0 m | 0 m | 5 m/s |
| 0,1 s | 0,50 m | -0,05 m | 0,45 m | 4 m/s | |
| 0,2 s | 1,00 m | -0,20 m | 0,80 m | 3 m/s | |
| 0,3 s | 1,50 m | -0,45 m | 1,05 m | 2 m/s | |
| 0,4 s | 2,00 m | -0,80 m | 1,20 m | 1 m/s | |
| 0,5 s | 2,50 m | -1,25 m | 1,25 m | 0 m/s | |
| Fallbewegung | 0,6 s | 3,00 m | -1,80 m | 1,20 m | -1 m/s |
| 0,7 s | 3,50 m | -2,45 m | 1,05 m | -2 m/s | |
| 0,8 s | 4,00 m | -3,20 m | 0,80 m | -3 m/s | |
| 0,9 s | 4,50 m | -4,05 m | 0,45 m | -4 m/s | |
| 1,0 s | 5,00 m | -5,00 m | 0 m | -5 m/s |
Fällt dir etwas auf, wenn du die Höhen über dem Boden und die Geschwindigkeiten in diesen Höhen vergleichst? (Beachte z.B. die Hervorhebungen)
2.) Der senkrechte Wurf mit Energieerhaltung erklärt.
2.1. Die Steigbewegung - energetisch betrachtet.
Wenn die Kugel unten mit vo abgeworfen wird, dann hat sie
zunächst eine (kinetische) Anfangsenergie von
Wstart = 1/2 * m * vo2.
Auf dem Weg nach oben wird die kinetische Energie immer
kleiner, denn die Kugel wird ja langsamer.
Dafür wird die Lageenergie größer, denn die Kugel
kommt ja immer höher.
In jeder Höhe ist die Summe aus kinetischer Energie und
Lageenergie gleich der Anfangsenergie.
Im höchsten Punkt kommt die Kugel für einen Moment zur Ruhe.
Sie hat dort keine kinetische Energie mehr, dafür ist die
Lageenergie maximal, es gilt dort WL = m
* g * hwurf.
2.2. Die Wurfhöhe.
Mit Hilfe des Energieerhaltungssatzes können wir die Wurfhöhe
hwurf auch berechnen, ohne dass wir dazu die
Bewegungsgleichungen brauchen. Es gilt nämlich:
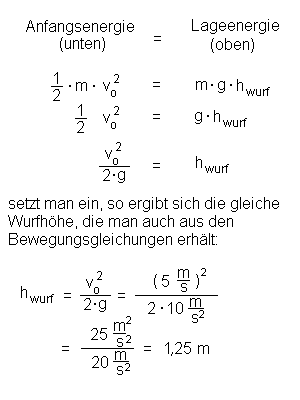
2.3. Die Fallbewegung - energetisch betrachtet.
Auf dem Weg nach unten (Fallbewegung) passiert das Gegenteil:
die kinetische Energie nimmt immer mehr zu und dafür
nimmt die Lageenergie immer mehr ab.
Am Boden angekommen ist die Lageenergie dann 0 und die gesamte Energie steckt
wieder in kinetischer Energie.
Sehen wir vom Luftwiderstand ab, so hat die Kugel am Boden wieder
die gleiche kinetische Energie, mit der sie gestartet ist, also auch
den gleichen Betrag der Geschwindigkeit!
Unterschiedlich ist lediglich die Richtung der Geschwindigkeit, also
das Vorzeichen:
am Anfang zeigt die Geschwindigkeit nach oben, bei der Fallbewegung nach
unten.
Weil in der Gleichung der kinetischen Energie Wkin = 1/2 *
m * v2 die Geschwindigkeit quadratisch vorkommt, spielt
für die kinetische Energie das Vorzeichen der Geschwindigkeit aber keine
Rolle!
2.4. Geschwindigkeiten in jeder beliebigen Höhe der Wurfbahn.
Nun wird auch verständlich, warum die Kugel in der gleichen Höhe
über dem Boden auch den gleichen Geschwindigkeitsbetrag haben muss:
Egal ob die Kugel sich nach oben oder unten bewegt, hat sie in der gleichen
Höhe auch die gleiche Lageenergie. Sie muss deshalb dort auch die gleiche
kinetische Energie haben, denn es gilt ja
Wkin = Wstart - WL. Damit hat sie
wegen Wkin = 1/2 * m * v2 dort natürlich
auch den gleichen Geschwindigkeitsbetrag!
Wenn du die Fragen und Aufgaben zum Applet sorgfältig durcharbeitest, solltest du diese Gedanken noch besser verstehen.
3.) Fragen und Aufgaben:
1. Die Simulation zur Tabelle von oben
Klicke einfach "Start" und schaue die Animation an.
Lass die noch einmal laufen, stoppe sie aber jeweils nach 0,1 s (also bei 0,1
s, 0,2 s, 0,3 s, .....) und notiere die Höhe über dem Boden, die
Geschwindigkeit, die kinetische Energie und die Lageenergie.
Du kannst dazu diese Tabelle ausdrucken oder auch gleich parallel dazu
einsetzen:
Arbeitsblatt Tabelle (WORD) ![]()
- Vergleiche deine notierten Werte mit der Tabelle von oben!
2. Die Masse wird verändert.
Belasse die Startgeschwindigkeit mit 5 m/s aber ändere die Masse der Kugel.
- Was ist nun gleich und was ist nun anders als vorher?
3. Veränderung der Energieanteile.
Ändere die Masse wieder auf 0,1 kg. Belasse die Startgeschwindigkeit bei 5 m/s.
- In welcher Höhe über dem Boden sind Lageenergie und kinetische Energie genau gleich?
- Kannst du das begründen?
- Warum ist die Geschwindigkeit in dieser Höhe nicht die halbe Startgeschwindigkeit (2,5 m/s)?
- In welcher Höhe über dem Boden hat denn die Kugel die halbe Startgeschwindigkeit?
4. Veränderung der Startgeschwindigkeit.
Im Feld für die Startgeschwindigkeit kannst du Zahlen eingeben. Es nimmt allerdings nur positive Geschwindigkeiten bis maximal 5 m/s an. Dezimalwerte gibst du bitte mit einem Punkt als Trennzeichen ein. Verändere nun diese Geschwindigkeit.
- Wie groß sind Anfangsenergie und Wurfhöhe, wenn du halbe Startgeschwindigkeit (2,5 m/s eingibst)
- Begründe dies!
- Bei welcher Startgeschwindigkeit ergibt sich halbe Anfangsenergie (0,625 J)?
- Wie groß ist die Wurfhöhe in diesem Fall? Begründe!
Hilfedateien für die Arbeiten mit dem Applet:
Arbeitsblatt zu den Aufgaben
(WORD) ![]()
Arbeitsblatt zu den
Aufgaben (PDF) ![]()
Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang
Christian und Mario Belloni vom Davidson College, USA
|


