Symmetrie beim senkrechten Wurf.
1.) Beschreibung des senkrechten Wurfs - Kräfte, Bewegungsart, Bewegungsgleichungen.
Der senkrechte Wurf einer Kugel setzt sich aus zwei Teilbewegungen zusammen:
| Steigbewegung (vom Boden zum höchsten Punkt) |
Fallbewegung (vom höchsten Punkt nach unten) |
|
| Bewegungsart | Es ist eine verzögerte Bewegung oder Bremsbewegung. | Es ist eine beschleunigte Bewegung |
| Kräfte | 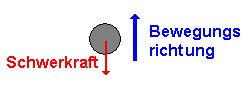 Die bremsende Kraft ist die Schwerkraft der Kugel. Sie wirkt nach unten (also entgegen der Bewegung). |
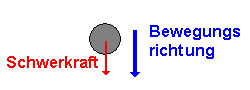 Die beschleunigende Kraft ist die Schwerkraft der Kugel. Sie wirkt nach unten (also in Bewegungsrichtung). |
| Verzögerung / Beschleunigung | Die Schwerkraft ist konstant, also ist es die Verzögerung auch, es ist die Fallgeschleunigung g. | Die Schwerkraft ist konstant, also ist es die Beschleunigung auch, es ist die Fallbeschleunigung g. |
| Bewegungsgleichungen | Es gelten folgende Bewegungsgleichungen: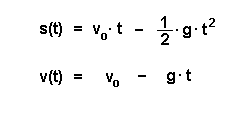 Die Höhe s(t) der Kugel bezieht sich auf den Startpunkt, also den Boden, sie ist immer oberhalb davon, also positiv. Ebenso zeigt die Geschwindigkeit immer nach oben (in die positive Richtung). Der zweite Anteil (g * t) wird nie größer als vo. Im höchsten Punkt ist v(t) = 0, also g * t = vo. |
Es gelten folgende Bewegungsgleichungen: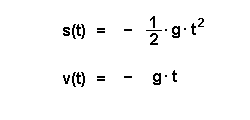 Das negative Vorzeichen bedeutet, dass die Fallhöhe vom höchsten Punkt aus bestimmt wird und nach unten zeigt. Ebenso ist die Geschwindigkeit nach unten gerichtet, sie ist also negativ. |
Mehr zum senkrechten Wurf und seinen Bewegungsgleichungen gibt es hier: Der senkrechte Wurf nach oben: Herleitung der Bewegungsgleichungen.
2.) Der zeitliche Verlauf der Bewegung mit den Bewegungsgleichungen.
In dieser Tabelle ist der senkrechte Wurf einer Kugel nach oben
zusammengestellt, die mit einer Anfangsgeschwindigkeit von
vo = 5 m/s abgeworfen wird. Als Fallbeschleunigung g wird
hier 10 m/s2angenommen.
Als Steigzeit ergibt sich dabei t = 0,5 s; die Steighöhe ist 1,25
m.
2.1. In zwei Tabellen getrennt
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.2. In einer Tabelle zusammengefasst.
Man kann auch nur die Gleichungen für die Steigbewegung benutzen und
die Zeit einfach "weiterlaufen" lassen.
Dies führt zum selben Ergebnis (verleiche den zweiten Teil ab 0,6s mit der
rechten Tabelle für die Fallbewegung, beide sind grau hinterlegt):
| Bewegungsanteil | Zeit t | gleichförmiger Anteil s1 = vo * t |
Fallanteil s2 = -1/2 * g * t2 |
Gesamtstrecke sges = s1 + s2 |
Geschwindigkeit v = vo - g * t |
| Steigbewegung | 0 s | 0 m | 0 m | 0 m | 5 m/s |
| 0,1 s | 0,50 m | -0,05 m | 0,45 m | 4 m/s | |
| 0,2 s | 1,00 m | -0,20 m | 0,80 m | 3 m/s | |
| 0,3 s | 1,50 m | -0,45 m | 1,05 m | 2 m/s | |
| 0,4 s | 2,00 m | -0,80 m | 1,20 m | 1 m/s | |
| 0,5 s | 2,50 m | -1,25 m | 1,25 m | 0 m/s | |
| Fallbewegung | 0,6 s | 3,00 m | -1,80 m | 1,20 m | -1 m/s |
| 0,7 s | 3,50 m | -2,45 m | 1,05 m | -2 m/s | |
| 0,8 s | 4,00 m | -3,20 m | 0,80 m | -3 m/s | |
| 0,9 s | 4,50 m | -4,05 m | 0,45 m | -4 m/s | |
| 1,0 s | 5,00 m | -5,00 m | 0 m | -5 m/s |
Fällt dir etwas auf, wenn du folgende Dinge vergleichst?
- Die Steigzeit (Zeit bis zum höchsten Punkt) und
Fallzeit (Zeit von dort bis zum Boden zurück),
- Wann sich die Kugel z.B. in 1,20 m Höhe befindet (zwei Mal!),
- Wann sich die Kugel jeweils in einer anderen Höhe befindet (z.B. 0,8 m),
- Welche Geschwindigkeiten die Kugel bei Steig- und Fallbewegung jeweils in
der gleichen Höhe hat.
(Beachte auch die Hervorhebungen)
Dass dies kein Zufall ist, kannst du nachprüfen, wenn du hier die
EXCEL-Tabelle herunterlädst, die diese Werte erzeugt hat.
senkrechter_wurf.xls ![]()
Setze eine andere Abwurfgeschwindigkeit ( < 5 m/s) ein und du wirst zur
gleichen Aussage gelangen.
Dahinter steckt der Energieerhaltungssatz.
Mehr dazu findest du auf dieser Seite:
Energieerhaltung beim
senkrechten Wurf.


