Eigenschaften einer Ellipse

Im Barock und im Rokoko waren ellipsenförmige Beete in den Gärten große Mode. Aber wie kann ein Gärtner eine Ellipse auf den Boden zeichnen?

Das geht mit der sogenannten "Gärtnerkonstruktion":

In zwei Punkten F1 und F2 werden Pflöcke in den Boden geschlagen, dann nimmt man eine Schnur, die länger als die Distanz zwischen den beiden Pflöcken ist. Die Enden der Schnur werden mit den Pflöcken F1 und F2 verknotet. Mit einem Schreibpfahl kann man dann die Ellipse zeichnen, wobei die Verbindungsschnur immer stramm gespannt bleiben muss.

Dies kannst Du hier mit einem Java-Applet ausprobieren, klicke dazu einfach auf "Start":

Fragen / Aufgaben:

Arbeite die Punkte selbstständig durch und versuche die Fragen zu beantworten. Wenn Du Probleme hast, dann gehe auf den zweiten Teil dieser Seite ("Ein wenig Theorie zur Ellipse") und hole Dir dort Ideen.
Gehe dann noch einmal zurück zum Java-Applet und mache Dir diese Aussagen klar.

1.) Klicke zunächst mit den Voreinstellungen einfach auf "Start" und sieh' Dir an wie die Gärtnerkonstruktion funktioniert.

2.) Die rote "Schnur" hat immer die gleiche Länge.
Probiere auch andere Einstellungen im Auswahlfeld "Kleine Halbachse" aus.

• Wie muss ein Gärtner vorgehen, wenn er eine "gestrecktere" Ellipse haben möchte?
• Wie muss er vorgehen, wenn er eine Ellipse haben möchte, die mehr einem Kreis ähnlich ist?
• Wie muss er vorgehen, wenn er genau einen Kreis haben möchte?
  Wo sind die beiden Pflöcke dann?

3.) Ein Kreis hat einen Radius, eine Ellipse hat eine große Halbachse a und eine kleine Halbachse b.
Klicke das Auswahlfeld bei "Halbachsen zeichnen" an. Nun werden beim Zeichnen die beiden Halbachsen a und b eingetragen.

• Wie verhalten sich die beiden Halbachsen bei einer "gestreckten" Ellipse?
• Wie verhalten sie sich bei einem Kreis?
• Warum kann man also einen Kreis als Sonderfall einer Ellipse betrachten?
• Was entspricht in diesem Fall dem Kreisradius r?

4.) Klicke "Reset". Vergleiche die Länge der roten "Schnur" mit der Länge der großen Halbachse a.

• Wie lang ist die Schnur im Vergleich zur großen Halbachse?

Ein wenig Theorie zur Ellipse.

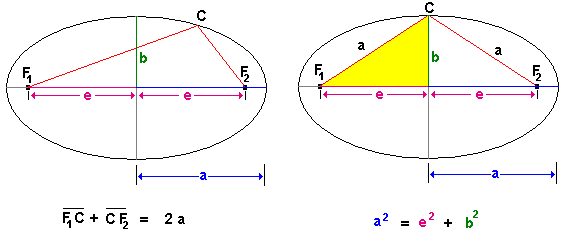
Ein Kreis hat einen Radius r, eine Ellipse hat zwei sogenannte Halbachsen, die große Halbachse a und die kleine Halbachse b.

Weiterhin hat eine Ellipse zwei Brennpunkte F1 und F2. Ihr Abstand vom Mittelpunkt der Ellipse ist e.

Eine Ellipse ist also die Menge aller Punkte, für die Entfernung von zwei gegebenen Punkten F1 und F2 konstant ist.
Die Länge der "Schnur" (rote Strecke in der Zeichnung) dabei konstant. Sie ist gleich zwei mal die Länge der großen Halbachse (2*a).

• Wie hängt die Entfernung e der Brennpunkte vom Mittelpunkt mit den beiden Halbachsen a und b zusammen?

Wählt man die Lage von Punkt C ("Pflock") so, dass er genau auf der kleinen Halbachse liegt, dann wird die Figur symmetrisch (Abbildung oben rechts).
Weil die gesamte Strecke von F1 über C nach F2 (die rot eingezeichnete Strecke) ja die Länge 2*a hat, ist die Entfernung von C nach F1 also a. Im gelb eingezeichneten Dreieck findet man dann mit Hilfe des Satzes von Pythagoras die Beziehung
a² = e² + b².

Der Kreis als Sonderfall einer Ellipse.

Je näher die beiden Brennpunkte F1 und F2 beieinander liegen, desto "kreisähnlicher" wird die Ellipse. Dies kann man sich klar machen, wenn man die Gleichung von oben nach e² auflöst. Es ergibt sich:

e² = a² - b².

Sind die beiden Halbachsen a und b gleich groß, dann ist e gleich 0, d.h. die beiden Brennpunkte F1 und F2 fallen dann zusammen und liegen im genau im Mittelpunkt.
In diesem Fall ergibt sich dann ein Kreis - er ist also ein Sonderfall einer Ellipse.

Numerische Exzentrizität.

Man bezeichnet den Quotienten e/a  =  epsilon auch als Exzentrizität der Ellipse.
Sind die Halbachsen gleich (Kreis), so ist epsilon = 0 (s.o.) - in diesem Fall ist also die Exzentrizität 0.
Bei einer sehr lang gestreckten Ellipse hingegen ist e fast so groß wie a - die Exzentrizität ist dann fast 1.

Je größer also die Exzentrizität, desto "gestreckter" ist die Ellipse.

Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang Christian und Mario Belloni vom Davidson College, USA (Copyright Hinweise) © Javascript dieses Problems: Klaus-Dieter Grüninger, Landesbildungsserver Baden-Württemberg, 2008