Das Gravitationsgesetz von Newton.

Newtons Apfel.

Als Johannes Kepler seine Gesetze der Planetenbewegung formulierte, war Sir Isaac Newton noch nicht einmal geboren.
Hätte Kepler schon gewusst, was Newton erst später herausfand, dann hätte er seine Gesetze auch mathematisch begründen können.

Newton erkannte, dass die Kraft, die den Mond in seiner Umlaufbahn um die Erde hält, im Prinzip dieselbe Kraft ist, die auch auf der Erde auf alle Körper wirkt - die Gravitationskraft (auch Gewichtskraft oder Schwerkraft genannt). Sie ist auch die Kraft, die z.B. einen Apfel vom Baum zur Erdoberfläche fallen läst. Ob Newton dabei ein Apfel auf den Kopf fiel, wie oft behauptet wird, ist nicht gesichert.

Die Gravitationskraft hängt von der Entfernung ab.

Betrachten wir einmal einen (sehr) kleinen Apfel, er möge die Masse 100g haben. An der Erdoberfläche zieht ihn die Erde mit der Kraft von 1 N an. Diese Kraft ist die Schwerkraft des Apfels. Im Anfangsunterricht hast Du gelernt, dass man diese Kraft als Masse m mal Ortsfaktor g berechnen kann (F = m*g).

Entfernt man einen Körper von der Erde, so wird diese Anziehungskraft kleiner.
Streng genommen verändert sich die Schwerkraft auch schon auf der Fallstrecke des Apfels vom Baum zur Erdoberfläche ganz geringfügig, aber davon sieht man meist ab.
Bringt man aber den Apfel weit hinaus in den Weltraum so ist der Effekt deutlich!

Der Apfel soll den Mond ersetzen.

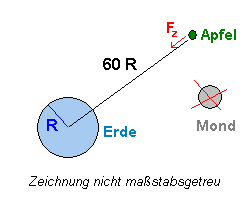
In Gedanken wollen wir den Apfel nun so weit von der Erde entfernen, dass er sich in der gleichen Entfernung vom Erdmittelpunkt befindet wie der Mond. Diese Entfernung ist etwa 384.000 km, was etwa 60 Erdradien entspricht. Wäre dabei der Apfel auch in den Nähe des Mondes, würde er natürlich auch noch vom Mond angezogen werden! Dann wirken zwei Anziehungskräfte auf den Apfel - eine die die Erde ausübt und eine die der Mond ausübt. Da wir uns nur mit der Kraft der Erde auf den Apfel beschäftigen wollen, denken wir uns den Mond einfach weg! Der Apfel übernimmt nun praktisch die Rolle des Mondes. Wäre der Apfel dort in Ruhe, würde er immer noch von der Erde angezogen werden und nach einiger Zeit auf die Erdoberfläche fallen (sofern er nicht in der Erdatmosphäre verglüht). Damit dies nicht passiert, muss der Apfel - genau wie der Mond - die Erde umkreisen und dabei die Erde einmal in 27,3 Tagen umrunden.

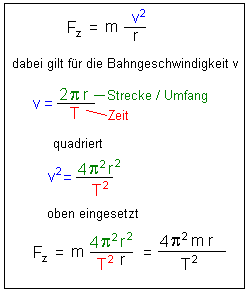Die Anziehungskraft der Erde auf den Apfel wirkt dann als Zentripetalkraft Fz und hält ihn auf seiner Umlaufbahn. Wir setzen in die Gleichung für r die Mondentfernung ein. Sie ist 60 Erdradien (r = 60 R). Dabei ist der Erdradius etwa 6400 km = 6.4*106 m. Die Entfernung r ist also 3,84*108 m. Die Masse des Apfels ist 100 g = 0,1 kg) und für T setzen wir die Umlaufzeit 27,3 d = 2,359 *106 s. Als Zentripetalkraft Fz erhält man dann 0,000272 N (2,724*10-4 N). Diese Kraft ist gerade 1/3600 der Kraft, die die Erde auf der Erdoberfläche auf den Apfel ausübt.

In 60-facher Entfernung wirkt also nur noch 1/3600 der Kraft. Also nimmt der Betrag der Gravitationskraft mit dem Quadrat der Entfernung ab, es gilt:

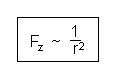
Doppelte Körpermasse - doppelte Gewichtskraft.

Hätte der Apfel doppelte Masse, so wäre auch die doppelte Zentripetalkraft nötig um ihn auf der Umlaufbahn zu halten. Also ist die Zentripetalkraft (und damit die Gravitationskraft) auch zur Masse m proportional.
Das ist ja auch schon auf der Erde so, dass auf einen Körper doppelter Masse m eine doppelt so große Schwerkraft wirkt.

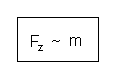
Auch die Größe / Masse des Zentralkörper spielt eine Rolle.

Du hast im Anfangsunterricht auch schon gelernt, dass die Schwerkraft auf dem Mond kleiner ist als auf der Erde. Dies liegt daran, dass der Mond ein kleinerer Himmelskörper ist, der auch eine kleinere Masse hat. Die Masse des Körpers, der die Schwerkraft ausübt, spielt also auch noch eine Rolle.
Hätte unsere Erde die doppelte Masse M, dann würde sie sowohl auf der Erde als auch in jeder anderen Entfernung auf jeden Körper die doppelt so große Anziehungskraft ausüben.

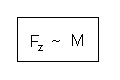
Wenn wir alle drei Abhängigkeiten zusammenfassen, dann erhalten wir folgende Gleichung:

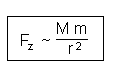
Um ein Gleichheitszeichen setzen zu können benötigen wir noch einen Proportionalitätsfaktor, er heißt Gravitationskonstante.
Dann ergibt sich Newtons Gravitationsgesetz:

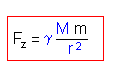
Durch Koeffizientenvergleich wirst Du feststellen, dass die blau gefärbten Größen zusammen das sind, was wir seither den Ortsfaktor g genannt haben. Wenn wir die Masse der Erde M wüssten, könnten wir die Gravitationskonstante Gamma angeben und umgekehrt.

Grafik Newton: GNU-Public-Licence, Autorin Theresa Knott
andere Grafiken und Gleichungen: Grüninger, Landesbildungsserver