Das erste Gesetz von Kepler.
1.) Auf welchen Bahnen bewegen sich Planeten?
Die Planeten bewegen sich um die Sonne. Die Sonne zieht sie an, sie übt eine Gravitationskraft auf die Planeten aus. Diese Gravitationskraft wirkt als Zentripetalkraft und sorgt dafür, dass der jeweilige Planet auf seiner (richtigen) Bahn bleibt.
Dasselbe passiert, wenn der Mond - oder ein Satellit - um die Erde kreist. In diesem Fall übt die Erde die Gravitationskraft aus.
Bei den Bahnen, auf denen sich die Planeten bewegen, denken wir zunächst an Kreisbahnen ( m ist die Masse des Planeten ).
Es gilt:  |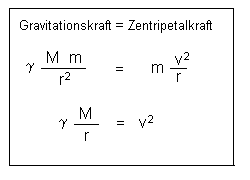
Die Gravitationskonstante Gamma und die Masse M des Zentralgestirns
(also z.B. der Sonne) ist für alle Planeten gleich. |
Das Java-Applet verdeutlicht dies. Die Zeit ist in Erdenjahre angegeben. Die Abstände von der Sonne sind im richtigen Maßstab dargestellt, jedoch nicht die Größe der Himmelskörper.
2.) Ein Meteoriteneinschlag - eine Katastrophe für einen Planeten?
- Ist die Kreisbahn die einzige Bahn, auf der sich Planeten bewegen können?
Sämtliche Planeten werden im Laufe ihrer Existenz immer wieder von großen und kleinen Meteoriten getroffen. So ist z.B. das Ries bei Nördlingen (direkt an der Grenze zwischen Baden-Württemberg und Bayern gelegen) ein großer Meteoritenkrater.
Nehmen wir einmal an, die Erde wird von einem großen Meteoriten "frontal" getroffen. Der Einschlag soll nicht so heftig sein, dass die Erde dabei zerstört wird. Wir wollen auch davon absehen, dass sich die Masse der Erde dadurch vielleicht vergrößert hat. Die Erde wird aber durch den Einschlag gebremst - ihre Bahngeschwindigkeit nimmt ab.
- Welche Folgen hat dies für die Bahn der Erde?
Wenn die Erde langsamer geworden ist, dann würde nun wegen
Fz = m * v2 / r eine geringere Zentripetalkraft
genügen, um die Erde auf ihrer Kreisbahn zu halten.
Die Gravitationskraft, die die Sonne auf die Erde ausübt, hat sich durch
den Meteoriteneinschlag (in gleicher Entfernung r) aber nicht
verändert.
Die Gravitationskraft ist also nun zu groß: Die Sonne
"zieht die Erde stärker an" als es für die Kreisbahn
nötig wäre.
Die Erde verlässt ihre Kreisbahn und nähert sich der Sonne.
Ein geringerer Abstand von der Sonne bedeutet aber nach unseren
Überlegungen von oben eine größere Bahngeschwindigkeit:
Die Erde wird also schneller, wenn sie mehr in Sonnennähe kommt - und
wieder langsamer, wenn sie sich wieder von der Sonne entfernt.
Weiterhin ändert sich die Umlaufdauer der Erde um die Sonne. Nach einem
Meteoriteneinschlag wäre also ein Erdjahr nicht mehr 365,25 Tage.
Das kannst Du im folgenden Java-Applet ausprobieren. Wähle im Auswahlfeld verschiedene Bahngeschwindigkeiten aus und beobachte die Auswirkungen auf die Bahnkurve, die gezeichnet wird, wenn Du "Start" klickst.
Die Bahn, auf der die Erde nun die Sonne umkreist, ist eine
Ellipsenbahn. Auf der Bahn ändert sich also die Entfernung von
der Sonne - und auch die Bahngeschwindigkeit der Erde auf ihrer Umlaufbahn.
Wie diese beiden Größen zusammenhängen, beschreibt dann das 2.
Gesetz von Kepler.
Das erste Gesetz von Kepler:
Planeten bewegen sich in der Regel auf Ellipsenbahnen um das Zentralgestirn. Kreisbahnen - als Sonderfall einer Ellipse - sind eher die Ausnahme. Das Zentralgestirn, z.B. die Sonne befindet sich dabei in einem der beiden Brennpunkte. |
Um die Idee verstehen zu können, wurden die Ellipsen im Applet
maßlos übertrieben! Die meisten Planetenbahnen in unserem
Sonnensystem sind sehr viel kreisähnlicher.
Sieh Dir dazu die
Seite von Walter Fendt
an und wähle die verschiedenen Planeten aus.
Was eine
Ellipse genau ist und wie man sie mathematisch beschreiben kann, erfährst
Du hier.
 |
Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang
Christian und Mario Belloni vom Davidson College, USA ( |