Das zweite Gesetz von Kepler.
Auf der Seite über
das erste Gesetz von
Kepler hast Du gelernt, dass sich Planeten auf Ellipsenbahnen um ihr
Zentralgestirn bewegen, so wie z.B. die Erde um die Sonne läuft.
In ganz seltenen Fällen ist die Umlaufbahn eine Kreisbahn. Dabei steht die
Sonne in einem Brennpunkt der Umlaufellipse.
Was eine Ellipse genau ist und wie man sie beschreiben kann,
kannst Du auf dieser Seite
erfahren.
Dort wird aber die Ellipse vom Zeichenpfahl des Gärtners mit konstanter
Bahngeschwindigkeit geschrieben. Bei einem Planeten, der auf einer Ellipsenbahn
um ein Zentralgestirn läuft, ist dies aber anders (s.u.).
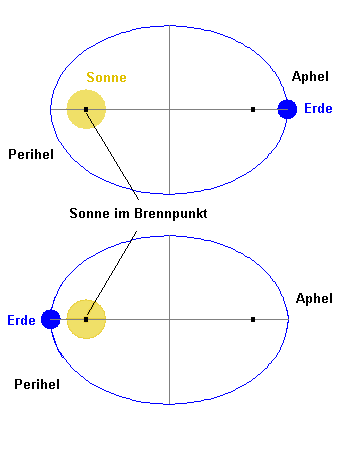 |
Die Sonne steht in einem der Brennpunkte der Ellipsenbahn. Zwei besondere Punkte der Erdbahn haben einen besonderen Namen:
|
Probiere hier den wirklichen Lauf eines Planeten um die Sonne in einer
Simulation aus.
Die Ellipsenformen sind hier auch wieder gegenüber richtigen
Planetenbahnen übertrieben um die Gesetzmäßigkeiten deutlich zu
machen.
Fragen und Aufgaben:
Die Bahngeschwindigkeit auf der Kreis- und Ellipsenbahn.
Beobachte die Bahngeschwindigkeit des Planeten. Wähle dazu im Auswahlfeld "Geschwindigkeit" verschiedene Einstellungen aus. Bei v = 2,2 ergibt sich eine Kreisbahn, bei den anderen Einstellungen Ellipsenbahnen.
- Bei welcher Bahnkurve ist die Bahngeschwindigkeit konstant, bei welcher nicht?
- Wenn sich die Bahngeschwindigkeit ändert, wo bewegt sich der Planet am schnellsten, wo bewegt er sich am langsamsten?
- Bei welcher der Ellipsenbahnen ist dies besonders deutlich?
Keplers Flächensatz.
Setze nun das Auswahlhäkchen bei "Fahrstrahl". Der Fahrstrahl
ist die Verbindungslinie Planet-Sonne.
In der Simulation wird der Fahrstrahl jeweils nach 1/10 der Umlaufzeit T
gezeichnet.
Wähle zunächst wieder die Kreisbahn (v = 2,2 ) als Einstellung aus und klicke "Start".
- Was kann man über die Fläche der Winkelsegmente ("Kuchenstücke") aussagen, die vom Fahrstrahl überstrichen werden?
- Erläutere, warum dies so ist.
Wenn sich ein Planet auf einer Ellipsenbahn um die Sonne
bewegt, dann ist seine Bahngeschwindigkeit dort groß, wo seine Entfernung
von der Sonne klein ist, und umgekehrt.
Wähle verschiedene Ellipsen und beobachte wieder die Fahrstrahlen und die
Flächen, die sie markieren genau.
- Was kann man nun über die in gleichen Zeitabständen überstrichenen Flächenstücke aussagen?
Das zweite Gesetz von Kepler:
Der Fahrstrahl (Verbindungslinie) Planet-Sonne überstreicht in gleichen Zeitintervallen gleich große Flächenstücke. |
Die Zusammenhänge mit dem Fahrstrahl bei verschiedenen Planeten kannst
Du auch auf der
![]() Seite von Walter Fendt zum 2.
Kepler Gesetz weiter erkunden.
Seite von Walter Fendt zum 2.
Kepler Gesetz weiter erkunden.
Interessantes:
Das Gesetz von Coulomb, das die Anziehung zweier ungleichnamiger,
punktförmiger Ladungen beschreibt, hat die gleiche "Bauform" wie
das Gravitationsgesetz, das die Anziehung zwischen zwei Massen beschreibt.
Daher bewegt sich z.B. eine Ladung um eine andere (ungleichnamige) Ladung
ähnlich wie ein Planet um die Sonne.
Diese Ähnlichkeit wurde hier im Applet ausgenutzt. Das Applet EField
beschreibt eigentlich die Bewegung von Ladungen im elektrischen Feld.
Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang
Christian und Mario Belloni vom Davidson College, USA ( |


