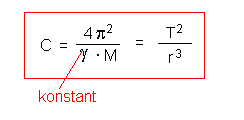Keplers drittes Gesetz und Newtons Gravitationsgesetz.

Wie Kepler sein drittes Gesetz fand.

Johannes Kepler (1571 - 1630) fand sein drittes Gesetz nicht durch theoretische Überlegungen, sondern durch "Probieren" mit Daten, die er aus genauen Beobachtungen der Planetenbewegung - insbesondere aus Prag von Tycho Brahe - hatte.

Kepler war ein tief religiöser Mensch und er ging davon aus, dass Gott die Schöpfung so gestaltet habe, dass der Mensch sie begreifen könnte - wenn er nur gut genug nachdachte.

Dabei ging er, wie wir heute auch noch, davon aus, dass die Natur einfach strukturierten Gesetzen unterliegt:
so, wie z.B. im Weg-Zeit-Gesetz einer beschleunigten Bewegung (s = 1/2 * a * t²) ein einfacher Exponent 2 - und nicht etwa so etwas wie 2,173 - vorkommt, so sollte auch ein Gesetz der Planetenbewegung einfach sein.

Er fand heraus, dass die Umlaufzeit eines Planeten um das Zentralgestirn zum Quadrat, geteilt durch die dritte Potenz seines Abstandes r davon, für alle Planeten die gleiche Konstante ergibt, man nennt sie die Keplerkonstante :

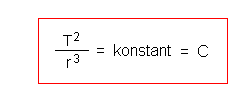
Johannes Kepler und Sir Isaac Newton.

Als Kepler 1618 sein drittes Gesetz formulierte, war Sir Isaac Newton (1642 - 1727) noch nicht einmal geboren.
Dieser formulierte sein Gravitationsgesetz im Jahre 1668, also ziemlich genau 50 Jahre nachdem Kepler sein drittes Gesetz fand - da war Kepler aber schon 38 Jahre tot!
Kepler und Newton waren also keine Zeitgenossen.

Hätten beide zur selben Zeit gelebt, dann wären sie vielleicht auch darauf gekommen, dass sich Keplers drittes Gesetz aus Newtons Gravitationsgleichung herleiten lässt.

Herleitung von Keplers drittem Gesetz aus dem Gravitationsgesetz von Newton.

Die Gravitationskraft Fg ist um so größer, je größer die Masse der beiden Körper ist, die einander anziehen.
Sie nimmt mit dem Abstand r der beiden Körperschwerpunkte quadratisch ab.
Damit die Einheiten passen, kommt noch die Gravitationskonstante Gamma ins Spiel.

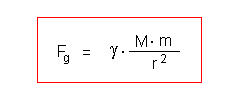
Wir betrachten nun die Gravitationskraft Fg, die die Sonne (Masse M) auf einen Planeten (Masse m - z.B. die Erde) ausübt.
Diese Kraft sorgt als Zentripetalkraft Fz dafür, dass die Erde in ihrer Umlaufbahn um die Sonne bleibt.
Wie man sieht, braucht man die Masse der Erde gar nicht zu kennen, sie kürzt sich heraus!

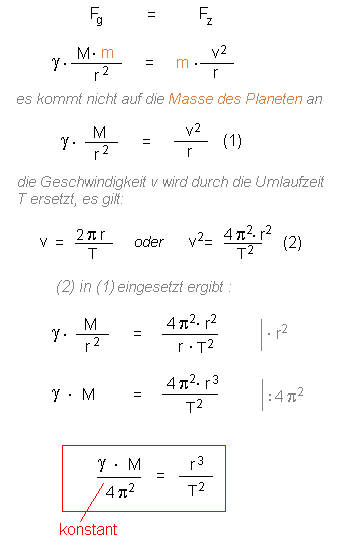
Alle Planeten in unserem Sonnensystem werden von der Gravitationskraft, die die Sonne auf sie ausübt, auf ihren jeweiligen Umlaufbahnen gehalten.
Der Faktor aus der universellen Gravitationskonstante Gamma, der Masse der Sonne M und 4 mal Pi zum Quadrat im Nenner ist also für alle Planeten gleich.

Dies ist offenbar genau der Kehrwert von Keplers empirisch gefundener Konstante (s.o.).
Bildet man die Kehrwerte gilt für die Keplerkonstante daher auch: