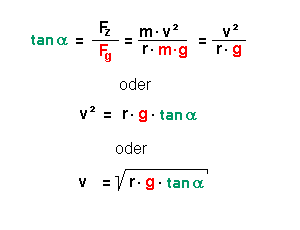Überhöhung von Kurven.

Der Zug steht schief ...?!

Der Zug steht schief! Steht der Zug auf diesem Foto nicht schief?
Doch, ganz eindeutig!

Das Bild zeigt einen Nahverkehrszug im Bahnhof von Göppingen-Faurndau auf der Filstalbahn.
Hier halten Züge eher selten. Auf der Filstalstrecke verkehren aber viele schnelle Züge auf der Fahrt von Stuttgart nach München.

Weiterhin fällt auf, dass der Bahnhof in einer relativ engen Kurve liegt.

Auf diesem Foto, nur 100 m weiter Richtung Göppingen aufgenommen, fällt dies noch mehr auf:
Die linken Schienen (Kurvenaußenseite) liegen gegenüber den rechten Schienen (Kurveninnenseite) erhöht.

  • Hat diese "Überhöhung" der Gleise damit zu tun, dass schnelle Züge dann besser durch die Kurve kommen?
  • Ist so die Abnutzung der Schienen weniger stark?
 Es geht in die Kurve!

Theoretische Überlegung zur Überhöhung:

Hier ist die Lokomotive noch einmal in einer (übertriebenen) Schemazeichnung dargestellt:

Nach unten wirkt senkrecht die Gewichtskraft Fg (rot). Nach oben, senkrecht zur Verbindungslinie der Schienen, wirkt die Kraft Fs von der Schiene auf die Lok (blau). Beide zusammen kann man durch die Zentripetalkraft Fz (schwarz) ersetzen, die horizontal wirkt.

In dem gelb unterlegten Kräftedreieck gilt dann:

Herleitung der Gleichung

 Die Lok im Schema (übertrieben)

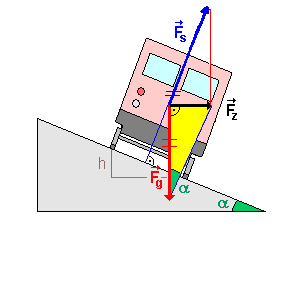Es spielt also gar keine Rolle, ob ein schwerer Güterzug oder ein vollbesetzter (oder ein leerer ICE) die Kurve befährt!
Weiterhin muss man stärker überhöhen, wenn eine größere Geschwindigkeit gefahren werden soll.
Auch der Radius der Kurve spielt eine Rolle, weite Kurven können schneller durchfahren werden als enge Kurven

Ein Beispiel:

Die Kurve habe einen Radius von 1000 m und sie soll für eine Idealgeschwindigkeit von 162 km/h ausgelegt sein (das sind 162 : 3,6 = 45 m/s). Nach der oberen Gleichung ergibt sich:
tan alpha = (45 m/s)2 / 1000 m * 10 m/s2 = 0,203 - was einem Winkel von etwa 11,45 Grad entspricht.

Bei dieser Geschwindigkeit ist die Abnutzung der Schienen minimal. Fährt der Zug langsamer, wird in dieser Kurve die rechte Schiene stärker abgenutzt, fährt er schneller die linke Schiene.

Überhöhung der Schiene

Um welche Strecke h muss dann die linke Schiene gegenüber der rechten Schiene überhöht werden?

Überhöhung der Schiene

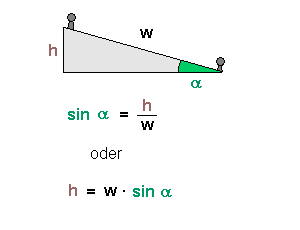Die Skizze links zeigt noch einmal einen Ausschnitt der Skizze von oben, jedoch ohne Lokomotive und Kräfte.

Die Spurbreite w der Normalspur bei uns in Deutschland ist 1435 mm = 1,432 m

Benutzt man den Winkel Alpha von 11,45 Grad (Ergebnis von oben) so erhält man h = 284,78 mm = 28,48 cm.

Alte Bahnstrecken folgten häufig Flussläufen. Hier musste man die Streckenführung so planen, wie die Topografie es vorgab. Machten Fluss und Tal eine enge Biegung, so musste die Trassenführung hier meist ebenfalls eine Kurve machen. Solche Passagen können nicht mit großer Geschwindigkeit durchfahren werden.
Neue Hochgeschwindigkeitsstrecken werden oft abseits der Bebauung quer durch die Landschaft geplant. Hier sind weitere Kurven und damit größere Geschwindigkeiten möglich.

Überhöhung auf der Radrennbahn

Ausschnitt Stuttgarter Sechstagerennen

Dieses Foto von Jochen Weiland ( www.jeweiland.net) zeigt eine Szene vom Stuttgarter 6-Tage-Rennen der Radprofis.
Das Rennen wird jährlich im Winter in der Hanns-Martin-Schleyer-Halle in Stuttgart ausgetragen.

Damit die Akteure flott ihre Runden drehen können, ist auch hier die Bahn überhöht. Die 285 m lange Bahn lässt Durchschnittsgeschwindigkeiten von etwa 60 km/h zu.

Dazu eine Rechenaufgabe:

Nehmen wir an, die Bahn sei kreisrund.
Um welchen Winkel muss die Bahn dann geneigt sein, damit der Winkel für eine Geschwindigkeit von 60 km/h optimal passt?

Wo wird ein Fahrer einen langsameren Fahrer überholen, oberhalb oder unterhalb von ihm? Begründe!

Bildernachweis: Bahnfotos - Klaus-Dieter Grüninger, Landesbildungsserver
6-Tage-Rennen - J. Weiland, Filderstadt