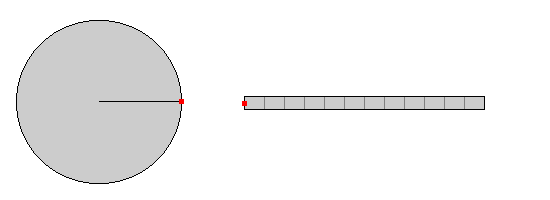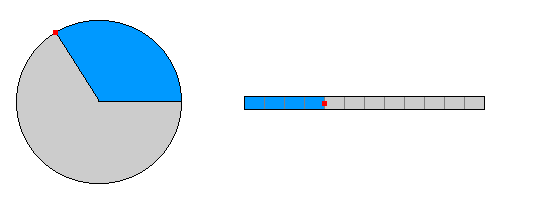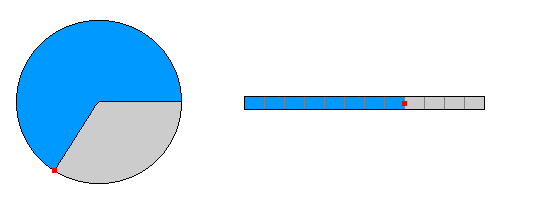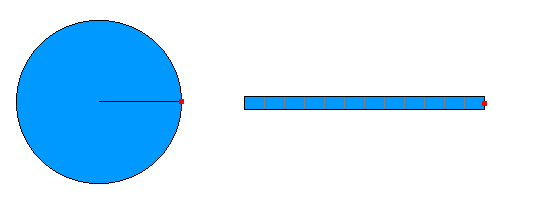
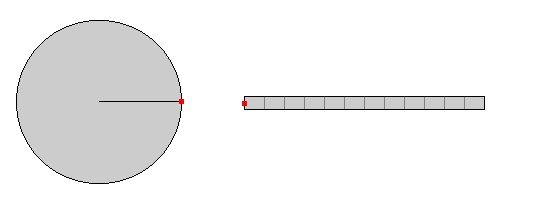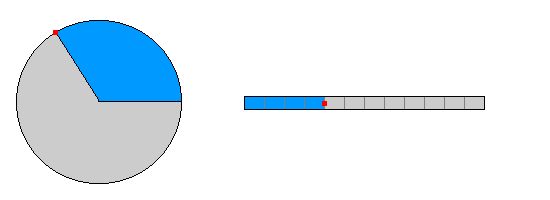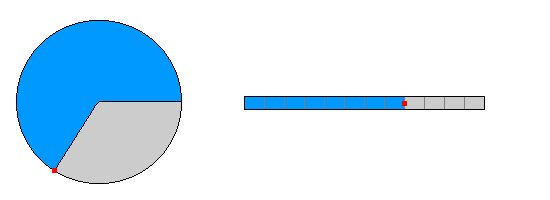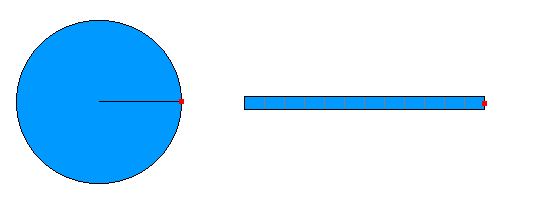
Vergleich: gleichförmige Kreisbewegung - lineare Bewegung
Die folgende Darstellung zeigt für die gleichförmige Kreisbewegung
bzw. die gleichförmige, lineare Bewegung des roten Punktes jeweils den Ort, an dem er zu
verschiedenen ausgewählten Zeitpunkten ist (eine Art Stroboskopaufnahme).
Der bereits zurückgelegte Winkel bzw.
Weg ist blau gezeichnet, der noch zurückzulegende Winkel
bzw. Weg ist grau eingefärbt.
| Kreisbewegung |
lineare Bewegung |
| Wegstrecken : In der doppelten Zeit legt der Punkt die doppelte Wegstrecke auf
dem Kreisbogen zurück. |
Wegstrecken : In der doppelten Zeit legt der Punkt die doppelte Wegstrecke
auf der Bahn zurück. |
| In gleichen Zeitintervallen (jeweils ein Bildwechsel) werden gleiche Wegstrecken auf dem Kreisbogen zurückgelegt.
|
In gleichen Zeitintervallen (jeweils ein Bildwechsel) werden gleiche Wegstrecken zurückgelegt.
|
| Winkel : In der doppelten Zeit überstreicht der Verbindungsstrahl Punkt-
Mittelpunkt den doppelten Winkel.
|
Was ist an dieser Darstellung anders?
Die
Darstellung läuft schneller ab, die Zeitintervalle
sind also kürzer.
Die Geschwindigkeit der linearen Bewegung und die Bahngeschwindigkeit der
Kreisbewegung werden dadurch größer.
Auch die jeweiligen Winkelsegmente werden schneller überstrichen, man
sagt, die Winkelgeschwindigkeit wird größer.
| Kreisbewegung |
lineare Bewegung |
| In jedem Zeitintervall Man nennt den Quotienten:
die Bahngeschwindigkeit der Kreisbewegung. |
In jedem Zeitintervall
Man nennt den Quotienten:
die Geschwindigkeit der linearen Bewegung. Die Einheit der Geschwindigkeit ist 1 m / s |
| Parallel dazu nennt man den Quotienten aus überstrichenem Winkel und dazu nötiger Zeit:
die Winkelgeschwindigkeit der Kreisbewegung. Die Einheit der Winkelgeschwindigkeit ist 1 Grad / s oder auch 1 / s. |
Verwandt heißt noch lange nicht gleich!
| Damit hat die Winkelgeschwindigkeit dieselbe Einheit wie die
(Dreh-)frequenz f, also 1/s oder Hz. |
Überlegen wir dazu weiter:
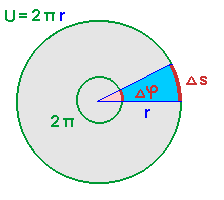
Nehmen wir an, das Winkelsegment sei 30 o, dann ist es gerade 1/12 der Gesamtwinkels von 360 o
Damit hat auch das Streckensegment
gerade 1/12 der
Länge des gesamten Kreisumfangs
U.
Ist die Bahngeschwindigkeit konstant, benötigt ein Teilchen also zum
Zurücklegen des Streckenelements
gerade die Zeit
, das ist hier 1/12 der gesamten
Umlaufzeit T.
Es gilt also für die Bahngeschwindigkeit:
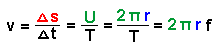
Da auch die Winkelgeschwindigkeit konstant ist, gilt für die Winkel
entsprechend:
Zum Überstreichen des Winkelsegments braucht der Verbindungsstrahl
die Zeit , dies ist hier gerade
1/12 der Zeit, die er zum Überstreichen des Gesamtwinkels benötigt. (Der Gesamtwinkel
wird üblicherweise im Bogenmaß angegeben).
Ein Vergleich der beiden Gleichung zeigt die wichtigen Beziehungen:
 |
und |
 |
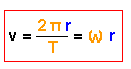... was ist denn nun konstant?
Da sich der ganze Kreis mit derselben Frequenz dreht - also die Umlaufzeit T fest liegt - ist auch für alle Punkte auf dem Kreis die Winkelgeschwindigkeit gleich groß !
Jedoch ist deren Bahngeschwindigkeit verschieden :
Je weiter sie vom Kreismittelpunkt entfernt sind - je größer also
der Radius r ist - desto länger wird auch der Weg (Kreisumfang), den sie
in der Zeit T zurücklegen müssen.
Die Bahngeschwindigkeit muß weiter außen also größer
sein.
Das sieht man ja auch an der Formel, denn v ist proportional zu r : Doppelt so
großer Abstand vom Mittelpunkt r bedeutet also doppelt so große
Bahngeschwindigkeit v.
Die Winkelgeschwindigkeit ist daher die geeignetere Größe um eine Kreisbewegung zu beschreiben.
Grüninger, Landesbildungsserver