Herleitung der Gleichung zur Zentripetalkraft.

Alle Größen sind Vektorgrößen. Aus technischen Gründen fehlen die Vektorpfeile über den Größen im Text und auch in den Grafiken.

Bahngeschwindigkeit : gleicher Betrag aber verschiedene Richtung.

Animation: zwei Bahnpunkte

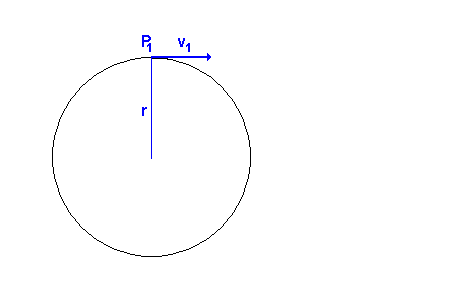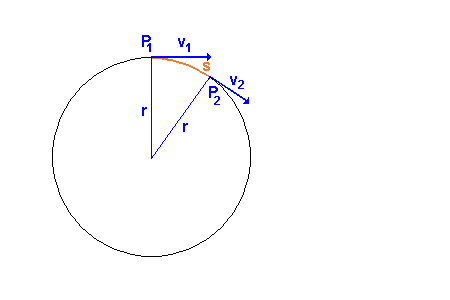Die nebenstehende Animation zeigt zunächst das umlaufende Teilchen im Punkt P1. Es bewegt sich im Uhrzeigersinn und hat dort die Bahngeschwindigkeit v1.

Nach einer Zeit Delta-t ist es im Punkt P2 angekommen. Es hat dabei die Strecke s auf dem Kreisbogen zurückgelegt.
Im Punkt P2 hat es die Bahngeschwindigkeit v2.
Der Vektor der Bahngeschwindigkeit steht stets senkrecht auf dem Kreisradius.

v1 und v2 sind vom Betrag her gleich groß. (Die Länge der Vektorpfeile ist gleich lang)
Der Betrag der Umlaufgeschwindigkeit ist konstant.

Jedoch ist die Richtung von v1 und v2 verschieden!

Die Geschwindigkeitsvektoren werden von einem Punkt aus gezeichnet.

Animation: Konstruktion des Geschwindigkeitsdreiecks

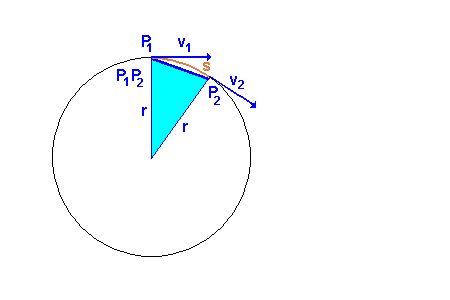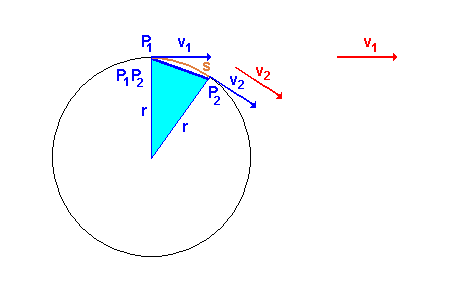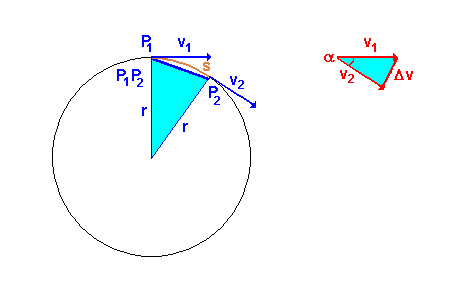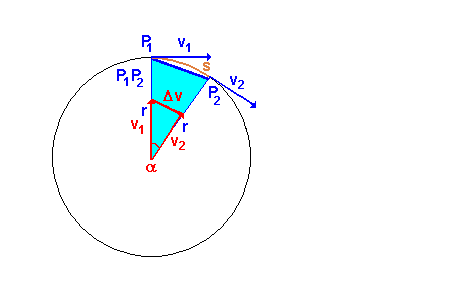Diese Animation entwickelt die Idee, wie man weiter vorgehen kann. Schaue sie Dir gut an, bis Du die Idee verstanden hast.

Zunächst wird der Geschwindigkeitsvektor v1 nach rechts hinaus kopiert.
Danach macht man dasselbe mit dem Geschwindigkeitsvektor v2
Die beiden Vektoren werden dabei einfach parallel verschoben.

Dann wird das rote Dreieck durch die Strecke Delta-v ergänzt.

Die Geschwindigkeitsänderung Delta-v ändert hier nicht den Betrag der Bahngeschwindigkeit, aber die Richtung.

Man sieht dann, dass die beiden Dreiecke ähnlich sind. Man kann das rote Geschwindigkeitsdreieck drehen und dann in das blaue Lagedreieck verschieben.

Die Ähnlichkeit wird ausgenutzt.

Ähnlichkeit der Dreiecke

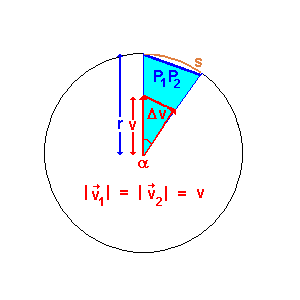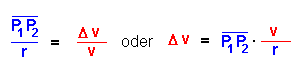
Nach dem zweiten Strahlensatz kann man folgende Beziehung aufstellen:
Die Länge der Sehne P1P2 verhält sich zum Radius r wie die Differenzgeschwindigkeit Delta-v zum Betrag der Bahngeschwindigkeit v.
(Beachte dabei die Beziehung für die Geschwindigkeitsvektoren und den Betrag der Geschwindigkeit in der Darstellung)

Man kann also schreiben:

Formel1

Betrachtet man nun zwei Punkte P1 und P2, die nahe beieinander liegen, dann unterscheidet sich die Länge des Kreisbogens s nicht sehr von der Länge der Sehne P1P2.
Weiterhin ist die Kreisbogenlänge s das Produkt aus dem Betrag der Bahngeschwindigkeit (also v) und der verstrichenen Zeit Delta-t (Die ersetzten Größen sind grau umrahmt).

Formel 2

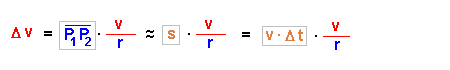
Wenn man dann noch die linke Seite und die rechte Seite der Gleichung durch Delta-t dividiert, erhält man:

Formel 3

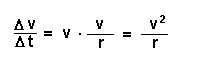
Macht man den Zeitabstand Delta-t immer kleiner, so wird einerseits die Kreisbogenlänge und die Sehnenlänge immer mehr angeglichen, andererseits ist der Quotient dann immer besser der Wert der Zentripetalbeschleunigung az, denn es gilt:

Beschleunigung und Limesbildung

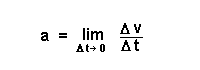
Also folgt:

Formel Zentripetalbschleunigung a=v²/r

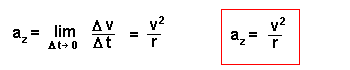
Die Zentripetalbeschleunigung verändert, wie schon oben gesagt, nicht den Betrag der Bahngeschwindigkeit, sondern ihre Richtung, so dass der Vektor der Bahngeschwindigkeit immer senkrecht zur Radiuslinie steht.

Bis zur Zentripetalkraft Fz ist es dann, mit Newtons zweitem Gesetz, nur noch ein kleiner Schritt:

Formel Zentripetalkraft Fz=m*v²/r

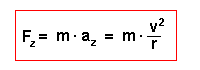
Grafiken und Animationen: Grüninger, Landesbildungsserver