Ein Boot fährt über einen See / Fluss.

Dies ist die virtuelle Version des "Bootsproblems" bei zusammengesetzten Bewegungen.

Für die Wiedergabe benötigt man die Java-Runtime-Environment. Wenn Sie diese nicht haben, können Sie sie hier kostenlos herunterladen externer Link.
In den Einstellungen des Browsers muss Javascript aktiviert sein.

Die Wasserfläche (blau) ist 200 m breit. Ein Boot (roter Punkt) überquert diese Wasserfläche. Es peilt dabei den Zielpunkt an (grüner Pfeil).
Die Länge des Pfeils steht für die Geschwindigkeit, die die Motoren des Boots entwickeln.

Die Ortskoordinaten lassen sich anzeigen, indem man die linke Maustaste gedrückt hält.

Eingabemöglichkeiten:

Für die Geschwindigkeit des Boots sind nur positive Zahlen möglich.

Eine Eingabe einer positiven Zahl bei "Fließgeschwindigkeit" lässt einen Fluss nach rechts "fließen", eine negative Zahl nach links.
Winkel 0 Grad bedeutet Geradeausfahrt, ein Winkel größer 0 Grad steuert nach rechts, kleiner 0 Grad nach links.

Zeichenoption:

Hier kann man wählen, was alles in der Zeichnung erscheinen soll.

Parameter: Zeichenoptionen:
Geschwindigkeit Boot :  

m/s

Fließgeschwindigkeit :  

m/s
Linie AB

v-Vektoren

Ansteuerwinkel :

1.) Wir überqueren einen See - Fließgeschwindigkeit=0 m/s.

Belasse zunächst alle Werte und klicke einfach "Start".

  • Das Boot (roter Punkt) überquert die Wasserfläche einfach von A nach B.
  • Wie lange benötigt es für die Überfahrt?
  • Wie hättest du diese Zeit berechnen können?
  • Wie lange dauert die Überfahrt, wenn das Boot mit 5 m/s fährt?

nach oben zum Applet

2.) Was passiert beim Überqueren eines Flusses?

Gibt nun für "Fließgeschwindigkeit" den Wert 2 m/s ein und klicke auf "Start".
Wenn du möchtest, kannst du zur Denkhilfe bei "Linie AB" ein Häkchen in die Checkbox setzen.

Das Boot peilt immer noch das gegenüberliegende Flussufer in B an.

  • Warum erreicht das Boot das andere Ufer nicht in B?
  • Kannst du berechnen, um welche Strecke es abgetrieben wird?
    (Kontrolliere deine Idee, indem du auf den roten Punkt am anderen Ufer klickst)
  • Um welche Strecke wird es bei der Fließgeschwindigkeit 3 m/s ; 4 m/s abgetrieben?

nach oben zum Applet

3.) Wie lange dauert die Überfahrt?

Vielleicht ist dir vorher etwas Überraschendes aufgefallen: die Überfahrt dauert immer gleich lang!

  • Warum ist dies so? Das Boot legt doch nun eine größere Strecke (quer) zurück?!

Aktiviere das Häkchen für die Anzeige bei "v-Vektoren" und wiederhole den Versuch.

Der grüne Vektorpfeil steht für die Geschwindigkeit, mit der die Motoren des Boots den Punkt B ansteuern.
Der blaue Pfeil steht für die Fließgeschwindigkeit des Flusses.
Der rote Pfeil steht für die Geschwindigkeit und Richtung, mit der sich das Boot tatsächlich bewegt.

  • Vergleiche die Länge (=Beträge der Geschwindigkeiten) des grünen und roten Pfeils.
  • Kannst du nun sagen, warum die Überfahrt trotz größerer Strecke nicht länger dauert?
  • Kannst du Ähnlichkeiten im (großen) Streckendreieck und (kleinen) Geschwindigkeitsdreieck entdecken? (Denke an den Strahlensatz!)

nach oben zum Applet

4.) Überfahrt auf direktem Weg.

Nun soll trotz einer Fließgeschwindigkeit des Flusses von 2 m/s das Boot im Punkt B ankommen.
Trage als Geschwindigkeit des Boots 4 m/s ein.

  • Was musst du dazu tun?
  • Welcher Ansteuerwinkel ist der richtige?
  • Wie ändert sich der Ansteuerwinkel, wenn die Fließgeschwindigkeit 3 m/s ist?
  • Was kann man über die Gesamtgeschwindigkeit des Bootes nun aussagen?
  • Warum dauert die Überfahrt nun länger als bei 3) ?
  • Warum kann das Boot (4 m/s) den Fluss gar nicht mehr direkt nach B überqueren, wenn die Fließgeschwindigkeit 4 m/s ist?
    (Betrachte den grünen und blauen Pfeil!).

nach oben zum Applet

5.) Den richtigen Ansteuerwinkel berechen.

Kannst du den richtigen Ansteuerwinkel für folgende Einstellungen berechen / vorhersagen?

Folgende Parameter seien gegeben:

  • Geschwindigkeit Boot: 3.5 m/s (vPeil)
  • Fließgeschwindigkeit : 1.5 m/s. (vFluss)
Vektorzerlegung der Peilgeschwindigkeit

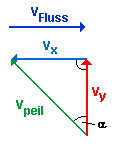Die nebenstehende Zeichnung soll dir beim Denken helfen.

Versuche zunächst den richtigen Winkel zu berechnen und prüfe dann erst dein Ergebnis in der Simulation nach.

Tipp:
Zerlege, die Geschwindigkeit des Boots (vPeil) in die Teilkomponenten vx und vy. (vy = vBoot)

Stelle dazu die nötigen Gleichungen auf.

Überlege danach, Richtung und Beträge von vx und der Fließgeschwindigkeit des Flusses. (vFluss)

Alles klar!?

nach oben zum Applet

Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:

Sie müssen dazu die gepackte Datei (boot.zip) herunterladen und in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder. Die nötigen Java-Achive sind ebenfalls enthalten.

Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.

Die Datei herunterladen : boot.zip gepackte Datei

Nutzungsbedingungen:

Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und Kollegen weitergeben.

Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der ausdrücklichen Zustimmung.

Physlets am Davidson College

Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang Christian und Mario Belloni vom Davidson College, USA (Copyright Hinweise) externer Link
© Javascript dieses Problems: Klaus-Dieter Grüninger, Landesbildungsserver Baden-Württemberg