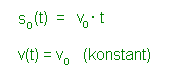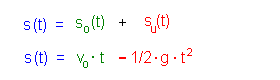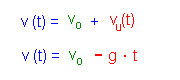Der senkrechte Wurf nach oben:
Herleitung der Bewegungsgleichungen.

1) Leben in einer Welt ohne Schwerkraft?

Stelle Dir vor, es gäbe keine Schwerkraft! Was würde mit einem Ball geschehen, den Du nach oben wirfst? Nun, er würde - nach einer kurzen Beschleunigungsphase durch Deine Hand - einfach in einer gleichförmigen Bewegung (also mit konstanter Geschwindigkeit vo) nach oben fliegen und schließlich die Erde in Richtung Weltraum verlassen. Etwas ähnliches passiert, wenn Astronauten in einem Raumschiff - etwa der ISS - einen Ball nach oben werfen. Dort herrscht auch beinahe Schwerelosigkeit - also das Fehlen von Schwerkraft. Allerdings ist dort der Flug des Balles nach kurzer Zeit zu Ende, wenn er gegen die Decke des Raumschiffs stößt und von dort wieder nach unten reflektiert wird! Für eine gleichförmige Bewegung nach oben gelten folgende Gesetze: Die zurückgelegte Wegstrecke und die Geschwindigkeit sind positiv gerechnet, weil sie nach oben erfolgen. Die Anfangsgeschwindigkeit vo in der Animation ist 4 m/s. Klicke in der Animation links einfach mehrmals auf "Weiter". Rechne die Werte nach!

2) Nun gibt es die Schwerkraft aber doch!

Wenn Du den Ball, statt ihn nach oben zu werfen, einfach fallen lässt, dann führt er einen Freien Fall aus. Mehr zum freien Fall findest Du  hier auf dem Landesbildungsserver. Den Einfluss der Luftreibung wollen wir im Folgenden vernachlässigen. Der freie Fall ist eine gleichmäßig beschleunigte Bewegung mit der Fallbeschleunigung g = 9,81 m/s2, die für alle Körper gleich groß ist. Der Zahlenwert der Fallbeschleunigung g hängt auch vom Körper ab, der die Schwerkraft ausübt, so ist g auf dem Mond ungefähr nur 1/6 so groß wie auf der Erde. Für den freien Fall gelten folgende Gesetzmäßigkeiten: Das negative Vorzeichen berücksichtigt dabei, dass die Bewegung nach unten, also in Richtung der negativen Vertikalachse erfolgt. Für die Animation wurde für g der Wert 10 m/s2 verwendet, damit es etwas einfachere Zahlenwerte gibt. Klicke in der Animation links einfach mehrmals auf "Weiter". Rechne auch hier wieder nach!

3) Der Wurf nach oben, ist eine Überlagerung beider Bewegungen.

beide Bälle ein Ball

Wenn Du einen Ball nach oben wirfst, wird er eine gewisse Höhe erreichen, für einen sehr kurzen Moment zur Ruhe kommen und dann wieder herunterfallen. Wie hoch der Ball dabei kommt, hängt davon ab, wie kräftig - also mit welcher Anfangsgeschwindigkeit vo- Du ihn nach oben wirfst. Er hat also sozusagen ein "Gedächtnis" für seine Abwurfgeschwindigkeit vo, dies ist die gleichförmige Bewegung nach oben aus 1). Der senkrechte Wurf nach oben ist nun eine Überlagerung der beiden Bewegungen aus 1) und 2). Links (grün) ist der Ball gezeichnet, wie er sich ohne Schwerkraft bewegen würde. Von der Strecke, die er bis zum jeweiligen Zeitpunkt gestiegen ist (grün) müssen wir die Strecke abziehen, die er zum gleichen Zeitpunkt gefallen ist (rot). Die tatsächliche Höhe des Balls ist dann die blau gezeichnete Strecke. Für die zurückgelegte Wegstrecke, ausgehend von Deiner Hand, gilt also: Für die Geschwindigkeit zum jeweiligen Zeitpunkt t gilt entsprechend: Klicke in der Animation links einfach mehrmals auf "Weiter" und vergleiche die Zahlenwerte mit denen aus 1) und 2).

4) Nun wird nur noch die wirkliche Bewegung alleine betrachtet.

Wähle nun in der Auswahlbox "ein Ball". Jetzt wird nur noch die tatsächliche Wurfbewegung des Balles angezeigt.

• Wann erreicht der Ball den höchsten Punkt?
• Was fällt Dir auf, wenn Du die Höhe zu den Zeitpunkten 0,3s und 0,5 s vergleichst?
• Was gilt für die Höhen zu den Zeitpunkten 0,2 s und 0,6 s, bzw. 0,1 s und 0,7 s?

5) Wie lange braucht der Ball, bis er den höchsten Bahnpunkt erreicht?
(Steigzeit t_s)

Im höchsten Bahnpunkt ist die Geschwindigkeit des Balles für einen kurzen Augenblick 0, bevor er sich auf den "Rückweg" macht. Der zweite Teil der Bewegung ist einfach der Freie Fall.

Für den höchsten Punkt gilt:

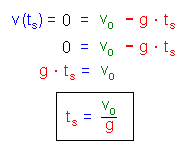
Ein Beispiel:
Wird der Ball mit einer Anfangsgeschwindigkeit von 4 m/s nach oben abgeworfen, so erreicht er den höchsten Punkt nach (vgl. Animationen):

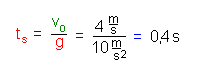
6) Wie hoch kommt der Ball? - Berechnung der Wurfhöhe h.

Wenn wir die Steigzeit t_s des Balles kennen, ist die Berechnung der Wurfhöhe h nun nicht mehr schwierig:
wir brauchen t_s nur in die Weg-Zeit-Gleichung (aus 3)) einzusetzen!

Dabei ergibt sich:

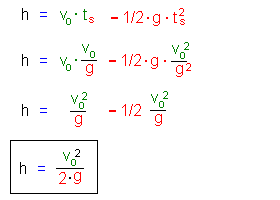
Für unser Beispiel ergibt sich dann eine Wurfhöhe von 0,8 m (Rechne nach!).
Bei doppelter Abwurfgeschwindigkeit kommt der Ball also vier mal so hoch!

7) Aufgaben zum Thema:

1)
Eines der Wahrzeichen von Genf ist eine große Fontäne im Genfer See, der "Jet d'Eau".
Recherchiere im Internet, wie hoch die Wassertropfen dort kommen. Bestimme daraus die Geschwindigkeit mit der die Wassertropfen die Düse verlassen (in m/s bzw. km/h).
Wie lange brauchen die Wassertropfen für diesen "Aufstieg"?

2)
Was passiert mit Gewehrkugeln, die mit sehr großer Geschwindigkeit in die Luft geschossen werden?
Kommen sie zurück, und falls ja, mit welcher Geschwindigkeit?

Dazu gab es einmal ein Folge der Reihe  "Kopfball" im WDR. Vielleicht findest Du sie im Internet noch als Podcast.

8) Weiterführende Fragen / Anregungen:

Wie würden wohl die entsprechenden Gleichungen für den Wurf eines Balles nach unten lauten?
Denke daran, dass dann die beiden Bewegungen gleichgerichtet und nach unten orientiert sind.

Wenn man die Darstellungen des senkrechten Wurfes nach oben um 90° im Uhrzeigersinn dreht, dann bekommt man die Simulation einer Bremsbewegung. Es ist der erste Teil der Bewegung, bis zu dem Zeitpunkt, in dem der geworfene Körper bzw. das gebremste Fahrzeug zur Ruhe kommt.

Der einzige Unterschied ist, dass die Bremsverzögerung a (statt der Fallbeschleunigung g) jeden beliebigen Wert annehmen kann, je nachdem wie heftig gebremst wird und wie gut die Beschaffenheit von Reifen und Straße ist. Bei der Wurfbewegung liegt die Fallbeschleunigung hingegen fest.

Sieh Dir dazu auch die  Seite zum Bremsweg auf dem Landesbildungsserver an und vergleiche die dort hergeleitete Formel mit den Gleichungen auf dieser Seite.

Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:

Sie müssen dazu die gepackte Datei (senkr_wurf.zip) herunterladen und in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder. Die nötigen Java-Achive sind ebenfalls enthalten.

Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.

Die Datei herunterladen : senkr_wurf.zip

Nutzungsbedingungen:

Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und Kollegen weitergeben.

Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der ausdrücklichen Zustimmung.

Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang Christian und Mario Belloni vom Davidson College, USA ( Copyright Hinweise) © Javascript dieses Problems: Klaus-Dieter Grüninger, Landesbildungsserver Baden-Württemberg