Der zentrale, elastische Stoß.
Für die Wiedergabe der Simulationen auf dieser Seite benötigt
man die Java-Runtime-Environment. Das Laden und Aktivieren der Java-Applets benötigt
etwas Zeit. |
1) Begriffsklärungen:
"Zentraler Stoß" bedeutet, die
Fahrzeuge treffen direkt aufeinander, so dass die Schwerpunkte auf einer Linie
liegen.
Die Fahrzeuge bewegen sich vor und nach dem Stoß auf dieser Linie.
Ein Gegensatz dazu wäre ein "versetzter Stoß", bei dem die
Fahrzeuge diese Linie verlassen.
Bei einem "elastischen Stoß"
bewegen sich die Fahrzeuge nach dem Stoßvorgang unabhängig
voneinander weiter, sie verhaken sich also nicht ineinander.
Solche Stöße gibt es z.B. beim Billard, bei Boxautos, oder wenn man
Münzen gegeneinander schießt.
Bei einem elastischen Stoß geht keine Energie verloren.
Energiehaltungssatz und Impulserhaltungssatz sind also beide erfüllt.
2.) Theorie des zentralen, elastischen Stoßes:
Für die Herleitung sei angenommen, dass das gestoßene Fahrzeug vor dem Stoß ruht (vB = 0). Der Index A bezeichnet das stoßende Fahrzeug, der Index B das gestoßene Fahrzeug. Geschwindigkeiten vor dem Stoß sind mit "v" bezeichnet, Geschwindigkeiten nach dem Stoß sind mit "u" bezeichnet. |
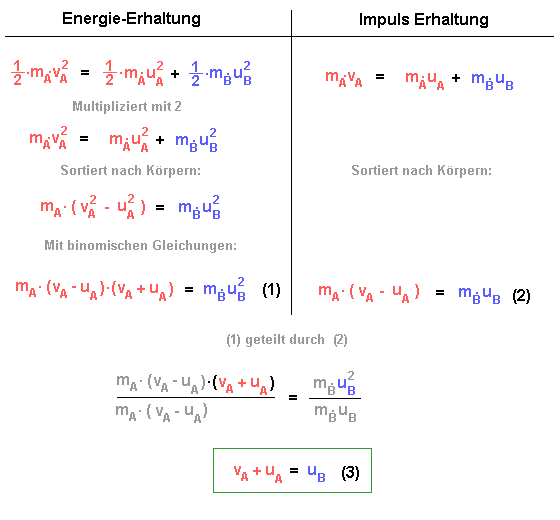
Für den letzen Schritt der Herleitung wurde die linke Seite von
Gleichung (1) durch die linke Seite von Gleichung (2) geteilt, ebenso die
rechten Seiten der beiden Gleichungen.
Faktoren, die sich herauskürzen, sind grau gedruckt.
| Die Summe der Geschwindigkeiten des stoßenden Fahrzeugs vor und nach dem Stoß, ist gleich der Geschwindigkeit des gestoßenen Fahrzeugs nach dem Stoß. |
3.) Probiere es mit dem Applet aus!
Der Wagen A (rot) fährt gleichförmig
mit einer Geschwindigkeit von 3 m/s auf den Wagen 2 zu.
Er muss vor dem Stoß eine Strecke von 1,5 m zurücklegen. Nach 0.5 s
prallt er auf Wagen 2 auf.
Wagen B (blau) ruht vor dem Stoß.
Die Masse von Wagen A und B kann gewählt werden.
Die Geschwindigkeit der Fahrzeuge wird angezeigt (Zahlenwerte über den
Fahrzeugen).
Probiere es aus und ändere auch die Massen der beiden Wagen!
4.) In der Gleichung steckt noch nicht alles!
Gegeben ist nur die Anfangsgeschwindigkeit des stoßenden Fahrzeugs vA (3 m/s).
Hingegen ist in der Gleichung (3) die Geschwindigkeit des stoßenden Fahrzeugs nach dem Stoß
(uA) und die Geschwindigkeit des gestoßenen Fahrzeugs nach dem Stoß
(uB) unbekannt.
Was bestimmt, diese Geschwindigkeiten??
Du vermutest sicher, dass dies von den Massen der Fahrzeuge abhängt:
- hat das stoßende Fahrzeug eine große Masse, das gestoßene
eine kleine Masse, dann wird das gestoßene Fahrzeug mit großer
Geschwindigkeit nach vorn weggestoßen.
Das ist, wie wenn du eine 2 Euro-Münze zentral auf ein 1 Cent-Stück stoßen lässt.
- hat das stoßende Fahrzeug eine kleine Masse, das gestoßene
Fahrzeug aber eine große Masse, wird das stoßende Fahrzeug nach
hinten zurückgeworfen.
Das ist, wie wenn du ein 1 Cent-Stück auf eine ruhende 2 Euro-Münze stoßen lässt.
Probiere es mal mit Münzen aus!!
Die Massen spielen eine Rolle!
Um die Geschwindigkeiten nach dem Stoß zu erhalten, setzen wir die Gleichung (3) und dieselbe Gleichung leicht umgeformt (3a) in den Impulserhaltungssatz (Gleichung 2) ein:

Fragen / Aufgaben :
Probiere folgende Fälle aus und überlege dir jeweils mit den Gleichungen, welche Geschwindigkeit die beiden Wagen nach dem Stoß haben:
- Wagen A und Wagen B haben gleiche Masse (1 kg, 2 kg, 3 kg).
- Wagen A hat doppelte Masse (2 kg) von Wagen B (1 kg)
- Wagen B hat doppelte Masse (2 kg) von Wagen A (1 kg)
- Wagen B hat dreifache Masse (3 kg) von Wagen A (1 kg)
- Welche Geschwindigkeiten haben die Fahrzeuge, wenn die Masse von Wagen A sehr groß gegenüber der Masse von Wagen B ist
- Welche Geschwindigkeiten haben die Fahrzeuge, wenn die Masse von Wagen B sehr groß gegenüber der Masse von Wagen A ist
Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:
Sie müssen dazu die gepackte Datei (elstoss.zip) herunterladen und in
ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder.
Die nötigen Java-Achive sind ebenfalls enthalten.
Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.
| Die Datei herunterladen : elstoss.zip ALT="gepackte Datei" BORDER="0" TITLE="gepackte Datei"> |
Nutzungsbedingungen:
Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern
gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und
Kollegen weitergeben.
Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der
ausdrücklichen Zustimmung.
Die Simulationen entstanden mit Hilfe von Physlets
von Wolfgang Christian und Mario Belloni vom Davidson College, USA (Copyright Hinweise) |


