Die Linsengleichung.
Für die Wiedergabe der Simulation auf dieser Seite benötigt
man die Java-Runtime-Environment. |
Beginne erst mit der Arbeit, wenn im Feld des Applets eine Linse (im Schnitt) mit Strahlen zu sehen ist.
Fragen / Aufgaben:
1.) Abbildung allgemein.
Wähle als Auswahl "Beide Strahlen". (Grundeinstellung).
Verändere den Ort des Gegenstandes (Pfeil) mit dem Regler
"Gegenstandsweite".
Die Gegenstandsweite g ist die Entfernung des Gegenstandes von der
Linsenmitte.
- Bei welcher Entfernung g ist die Bildgröße B größer als die Gegenstandsgröße G?
- Bei welcher Entfernung g ist die Bildgrößer B kleiner als die Gegenstandsgröße G?
- Bei welcher Entfernung g sind Bild und Gegenstand gleich groß?
Verändere nun auch die Brennweite f der Linse.
- Warum hat dies auch einen Einfluss darauf, wo das Bild entsteht?
Wie wollen nun den Mittelpunktsstrahl und den Achsenparallelen Strahl getrennt betrachten, damit wir uns auf das Wesentliche der Geometrie konzentrieren können. |
2.) Die Abbildungsgleichung bei der Sammellinse.
Wähle in der Darstellung "Mittelpunktsstrahl" aus und
klicke auch "Reset".
Die Brennweite f der Linse ist nun wieder 10 cm.
Bei einer Gegenstandsweite von 20 cm sind Gegenstand G und Bild B gerade
gleich groß. Der Abbildungsmaßstab A ist dann genau 1. |
Verschiebe den Gegenstand mit dem Regler "Gegenstandsweite".
- Bei welcher Gegenstandsweite g wird der Abbildungsmaßstab A größer 1?
- Bei welcher Gegenstandsweite g wird der Abbildungsmaßstab A kleiner 1?
- Bei welcher Gegenstandsweite g wird der Abbildungsmaßstab A genau 1?
Mache dir mit der Simulation folgenden Zusammenhang klar:
Nach den Strahlensätzen gilt:
![]()
3.) Die Brennweite f kommt ins Spiel.
Wie eine Linse abbildet, hängt aber sicher auch von ihrer Form und Wölbung ab, welche die Brennweite f einer Linse bestimmen.
Wähle nun für die Darstellung "Achsenparalleler Stahl" aus.
Der Gegenstand ist nun noch einmal als gedankliche Hilfe in die Mitte der Linse gezeichnet.
- Ändere die Gegenstandsgröße G (Regler mitte) und überzeuge dich, dass dieses "Hilfsbild" des Gegenstandes in der Linse genau so groß wie der Gegenstand selber bleibt.
Wie erhalten genau wie bei 2.) wieder ein System von zwei ähnlichen
Dreiecken.
Die beiden Abschnitte auf der optischen Achse sind diesmal:
- die Brennweite f (Abstand des Brennpunkts von der Linsenmitte) - links vom Brennpunkt
- die Differenz zwischen der Bildweite b und der Brennweite f (also b-f) - rechts vom Brennpunkt.
Verändere die Brennweite f mit dem Regler "Brennweite". Auch das verändert die Bildgröße B und die Bildweite b!
Wir finden diesmal als Zusammenhang:
![]()
4.) Die beiden Erkenntnisse werden zusammengenommen.
In beiden Gleichungen tritt der Abbildungsmaßstab A, also der Quotient B/G auf.
Die beiden Gleichungen können gleichgesetzt und umgeformt werden:
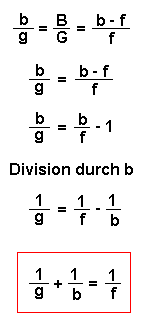
Die eingerahmte Gleichung heißt
"Linsengleichung".
Sie stellt einen Zusammenhang zwischen der Gegenstandsweite g, der Bildweite b
und der Brennweite der Linse f her.
Diese Seite können Sie in Ihrem Unterricht auch ohne einen Internet-Zugang nutzen:
Sie müssen dazu die gepackte Datei (linsengleichung.zip) herunterladen
und in ein Verzeichnis entpacken.
Das Paket enthält die Internet-Seite und alle darauf befindlichen Bilder.
Die nötigen Java-Achive sind ebenfalls enthalten.
Ihr Browser muss aber genauso für die Wiedergabe von Javascript und Java eingerichtet sein.
| Die Datei herunterladen :
linsengleichung.zip |
Nutzungsbedingungen:
Der Inhalt der Zip-Datei darf auf Einzelrechnern und Schulservern
gespeichert werden.
Sie dürfen die Dateien für Unterrichtszwecke an Kolleginnen und
Kollegen weitergeben.
Beachten Sie aber bitte unbedingt das Copyright der Autoren.
Sie dürfen den Inhalt der Seite nicht verändern.
Eine Publikation der Seite, in welcher Form auch immer, bedarf der
ausdrücklichen Zustimmung.
Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang
Christian und Mario Belloni vom Davidson College, USA ( |


