Freier Fall einer Kugel, Fallbeschleunigung

Wenn die Aufzeichnung von beschleunigten Bewegungen möglich ist, dann müsste es doch im Prinzip auch möglich sein, Fallexperimente mit der Lichtschrankenschiene durchzuführen, wenn man diese senkrecht stellt und einen geeigneten Gegenstand durch den Zwischenraum fallen lässt.

Zunächst war ich von meiner Idee begeistert, dann aber auch sofort skeptisch:

• Geht das überhaupt?
• Sind die Soundkarte und der Auswertrechner schnell genug dafür?
• Wird die Genauigkeit der Messerfassung ausreichen?
• Wie kann man den Gegenstand dazu bringen genau im Zwischenraum zwischen den Lichtschranken zu fallen?
• Welchen Einfluss hat die Luftreibung?
• Welche weiteren Probleme könnten auftreten?

1.) Messparameter und programmtechnische Vorüberlegungen.

Lässt man einen Gegenstand frei fallen, so benötigt er für eine Fallstrecke von 0,9 m eine Zeit von 0,43 s (s = 1/2*g*t²). In dieser Zeit muss der Rechner zehn Verdunklungen der Lichtschranken sicher erkennen, auswerten und speichern. An der letzten Lichtschranke wird eine Geschwindigkeit von 4,2 m/s erreicht. Bei einem Durchmesser einer Kugel von 10 mm entspricht dies also einer Verdunklungszeit von etwa 2,3 ms.

Übliche Soundkarten tasten mit 44100 Samples pro Sekunde ab, d.h. sie erfassen 44100 Spannungswerte je Sekunde und wandeln sie digital um.
Dabei entfällt die Hälfte - also 22050 Messungen je Sekunde - auf jeden Kanal. Hat das abgetastete Tonsignal eine Frequenz von 5 kHz, so entspricht dies einer Periodendauer von 0,2 ms. Während dieser Zeit werden also 0,0002 s* 22050 1/s = 4,41 Messwerte erfasst. Dies genügt noch, um das Signal sicher zu erkennen. (Shannon Theorem)

Während 2,3 ms Verdunklungsdauer erzeugt der Tongenerator der Lichtschrankenschiene etwa 10 Perioden. Dies müsste sicher zu messen sein. Allerdings kann man das Signal nur auf eine Periode genau auswerten. Man muss also bei so kurzen Zeiten mit einem systembedingten Fehler von bis zu 10% rechnen. Dennoch sollte das funktionieren und 10% Messfehler sind gerade noch zu ertragen.

2.) Experimentelle Vorüberlegungen.

Man kann einen Körper (idealerweise eine Kugel) nur dann dazu bringen, genau zwischen den Lichtschranken durchzufallen, wenn man ihm den Weg mit einer Röhre vorgibt. Meine Idee war also, ein durchsichtiges Acrylglasrohr genau zwischen den Lichtschranken zu positionieren und eine Kugel geeigneten Durchmessers durchfallen zu lassen.
Ich hatte keinen Zweifel, dass es mir gelingen würde, das Rohr genau genug zu justieren, dennoch hatte ich Bedenken, ob das überhaupt klappen könnte:

• Würde das runde Acrylglasrohr die Lichtstrahlen überhaupt durchlassen?
• Wirkt das Acrylglasrohr so stark als Linse, dass kein Lichtempfang mehr möglich ist?
• Würde ich in das Rohr Löcher für den Lichtstrahl bohren müssen?

Welchen Durchmesser sollte die Kugel haben?

• Ist sie zu klein, dann "pendelt" sie unter Umständen durch das Rohr und verdunkelt die einzelnen Lichtschranken nicht immer mit dem gleichen Durchmesser, was zu Messfehlern führt.
• Passt die Kugel aber gerade durch das Rohr, welchen Einfluss würde dann auftretende Reibung haben?
• Würde nicht die Luft, die die Kugel im Rohr vor sich herschiebt und die dann nicht an der Kugel vorbeiströmen kann, den Fall der Kugel zu sehr bremsen?

Die Probleme lagen auf der Hand, aber die Fragen ließen sich nicht theoretisch beantworten, das musste ich schlicht ausprobieren!

Ich besorgte mir über das Internet Plexiglasrohre mit 13 mm Außen - und 10 mm Innendurchmesser mit 1,0 m Länge. Solche Plexiglasrohre gibt es z.B. bei Ebay. Ich habe meine Rohre hier besorgt (Quelle: Online-Work-Shop, Frank Mannagottera, 82362 Weilheim/Obb.). Diese Rohre kosten ein paar Euro.

Als ich das Plexiglasrohr zwischen die Lichtschranken brachte, gab es die erste (positive) Überraschung: das Licht geht noch durch und die Lichtschranken reagieren auf einen Gegenstand im Rohr!

Als Halterung besorgte ich mir daraufhin Plastikhalter für 12 mm Kupferrohre oder 12 mm Elektrorohre im Baumarkt. Die Halterungen werden mit der Aluminium Halteplatte verschraubt. Dazu dient eine 6 mm Gewindeschraube (30 mm lang) mit Flügelmutter - ebenfalls aus dem Baumarkt - und eine kleine 13 mm lange Abstandshülse, die ich mir aus einem passenden Aluminiumrohr mit 8 mm Innendurchmesser sägte (vgl. Foto). Je nachdem, welche Distanzbolzen Sie zwischen den U-Rohren und dem großen Halteblech verwendet haben, müssen Sie die Gewindestangen ggf. etwas absägen und die Abstandshülse etwas kürzer machen.

Die beiden folgenden Bilder verdeutlichen, wie das Plexiglasrohr im Zwischenraum befestigt wird. Es genügen zwei Halteclips, weil das Acrylglasrohr mit 1,5 mm Wandstärke verwindungssteif genug ist. Die Halteclipse werden genau zwischen zwei Lichtschranken angebracht, d.h. zwischen Lichtschranke 3 und 4 bzw. Lichtschranke 7 und 8. Bitte darauf achten, dass das Rohr mit seiner "dicksten Stelle" genau zwischen den Lichtschranken liegt. Der Abstand des Rohr zur Halteplatte muss genau gleich sein, damit die Kugel nicht schräg durch die Lichtschranken läuft. Der seitliche Abstand ist weniger kritisch, ggf. muss man den Halteclip etwas abfeilen.

Dieses Bild zeigt die Verschraubung an der Trageplatte der Lichtschrankenschiene. Man erkennt die Flügelmutter und den Abstandshalter. Man kann auch gerade noch die Oberkante des Halteclip entdecken, in den das Rohr eingeclips wird.

3.) Der erste Test mit einer kleinen Schraube.

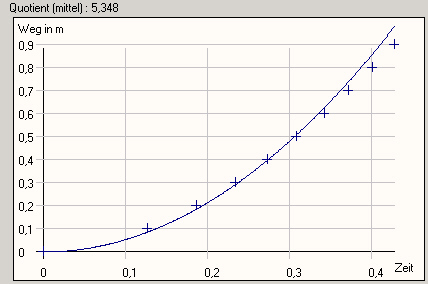Als ersten Test ließ ich eine kleine Schraube durch das Rohr fallen. Es funktioniert! Sogar mein alter 300 MHz Pentium II Laptop (Soundkarte eingebaut) war schnell genug für die Messung. Die Messwerte für die s-t-Auswertung waren - für das einfache Experiment - überraschend ordentlich. Als Quotient C = s / t2 ergab sich hier 5,3 m/s2, was einer Fallbeschleunigung von 10,6 m/s2entspricht. Bessere Werte bekommt man bei Fallexperimenten auf andere Art oft auch nicht heraus.

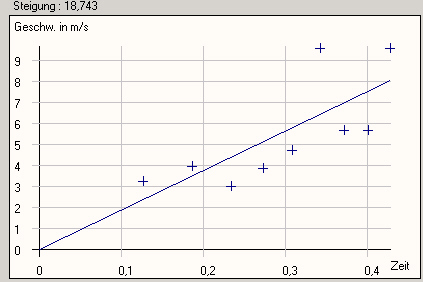Wie zu erwarten, war allerdings die v-t-Auswertung nicht zufriedenstellend: die Schraube "torkelt" während des Falls durch das Rohr, was dazu führt, dass die Verdunklungsbreite stark variiert. Dementsprechend streuen die Geschwindigkeitswerte stark. (vgl. Auswertung)

4.) Fallexperimente mit Kugeln.

Zwei Tage später trafen die Kugeln ein, die ich ebenfalls über Ebay besorgt hatte. Das waren einerseits Edelstahlkugeln mit 9,525 mm Durchmesser, die gerade so durch das Rohr passen (vgl. Foto) und Holzkugeln mit 8 mm Durchmesser. Die 40 Edelstahlkugeln kosteten mich incl. Versand nur etwas mehr als 5 Euro. (Quelle: Ebay: kugeln_winnie, Winfried Klarmann, Bamberg)

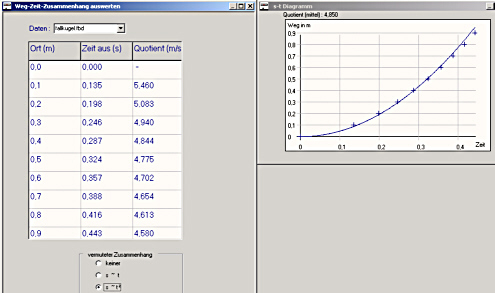
Mit den Messergebnissen der Stahlkugeln war ich recht zufrieden. Die Zeiten kommen ein klein wenig zu groß heraus, was an der Reibung oder am Luftstau liegen kann. (Mittlere Tabellenspalte 0,443 s für 0,9 m statt 0,428 s) Der Quotient für C = s / t2 liegt hier zwischen 4,58 m/s2und 5,08 m/s2, wenn man vom ersten Wert absieht. Im Mittel ergab sich 4,85 m/s2, was einer Fallbeschleunigung von 9,7 m/s2 entspricht.

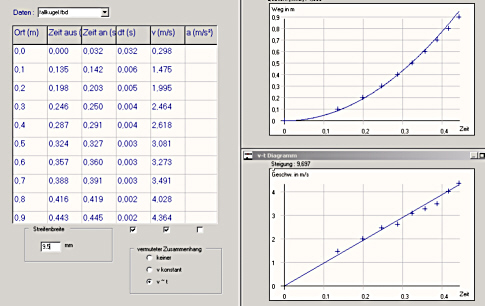Beim v-t-Diagramm ergibt sich schon eine halbwegs brauchbare Gerade. Die Geschwindigkeit im letzten Punkt ist mit 4,36 m/s etwas zu groß gegenüber der Theorie (4,2 m/s). Dies kann an der 10% Messabweichung liegen, die auswertungsbedingt entstehen kann (s.o.). Die mittlere Geradensteigung (a = v / t) ergibt sich zu 9,69 m/s2. Das passt sehr gut zum Ergebnis von oben.

Mit den Ergebnissen der Holzkugeln war ich hingegen nicht zufrieden. Sie sind zu leicht. Hier macht sich doch die Luftreibung deutlich bemerkbar. Meine Idee war eigentlich zu zeigen, dass es nicht vom Material (und damit von der Masse der Kugeln) abhängt, wie lange die Fallbewegung dauert, das gelingt sehr schlecht. Viel entscheidender als mögliche Auswertfehler und Luftwiderstand ist aber der geeignete Start der Kugeln und die wirklich senkrechte Justierung der Lichtschrankenschiene, damit keine Reibung an den Wänden auftritt. Ich habe alle Experimente zunächst "frei Hand" gemacht. Die Kugel sollte dann direkt über der ersten Lichtschranke mit dem Fall beginnen. Beginnt man zu hoch, dann hat sie schon Geschwindigkeit, wenn sie die Startlichtschranke erreicht, die Zeiten sind dann zu klein. Verdunkelt die Kugel schon bevor man loslässt, dann fallen die Zeiten wegen der "Schrecksekunde" deutlich zu groß aus. Deutlich besser ist es natürlich wenn man die Lichtschrankenschiene stabil über eine Stativstange befestigt und genau senkrecht ausrichtet (ggf. Wasserwaage oder Lot verwenden). Das nebenstehende Bild zeigt einen möglichen Aufbau. Die gelbe Wanne fängt die Kugel auf. Das Ende der Schiene ist etwas über der Wanne, damit die Luft im Rohr entweichen kann.

5.) Möglichkeiten für die Auslösung des Starts.

1) Der Trick mit der Büroklammer.

Die wahrscheinlich beste und einfache Anordnung für die Auslösung der Kugel ist es ein kleines 1 mm Loch durch das Plexiglasrohr zu bohren. Durch dieses steckt man eine aufgebogene Büroklammer. Die Kugel kann darüber eingelegt werden und wird so gehalten. Man justiert das Plexiglasrohr durch Ziehen oder Schieben so, dass die Startlichtschranke gerade noch nicht verdunkelt wird und die Kugel und die Büroklammer genau darüber sind (vgl. Foto). Zieht man die Büroklammer aus dem Loch, ist die Kugel frei und fällt. Auch wenn man sich nicht allzu viel Mühe mit dem Justieren gibt, wird man doch in der Regel für die Fallbeschleunigung zwischen 9,7 und 10,1 m/s2 herausbekommen. Größere Abweichungen hatte ich bei meinen Messungen praktisch nie.

2) Ein Haltemagnet für die Kugeln.

Bei kommerziellen Messeinrichtungen für den freien Fall werden die Kugeln meist mit Elektro-Haltemagneten gehalten. Es ist nun etwas schwierig Elektro-Haltemagnete aufzutreiben, die weniger als 20 mm im Durchmesser haben und daher noch zwischen die Lichtschrankenschienen passen.

Eine mögliche Bezugsquelle für einen geeigneten kleinen Haltemagneten ist http://www.respotec.de. In deren Programm gibt es den Haltemagnet Re06510, der 17 mm Durchmesser und 10 mm Höhe hat. Er kostet etwa 2,60 Euro zzgl. Versandkosten (Stand März 2008).
Der Haltemagnet passt zwischen die Lichtschrankenschienen und ist bei 1,5 bis 2,0 V angelegter Spannung durchaus in der Lage die Stahlkugel sicher zu halten. Dabei wird die Spule auch noch nicht übermäßig heiß. (Stromstärke etwa 0,5 A)
Möchte man den Haltemagneten verwenden, muss man das Plexiglasrohr an einer Stelle etwas ausnehmen.
Die Kugel wird zunächst mit einer Art kleinem "Löffel" bei eingeschaltetem Elektromagneten unter den Haltemagneten gebracht. Die Kugel fällt dann beim Öffnen des Stromkreises.

Die Messwerte sind mit dem Haltemagneten geringfügig genauer als mit der Büroklammer-Methode, möglicherweise weil beim Herausziehen der Büroklammer die Kugel in Rotation versetzt wird.

Fazit:

Mit der Lichtschrankenschiene gelingt es auch erfolgreich Fallexperimente durchzuführen, wenn man sie senkrecht stellt. Mit geeigneten Stahlkugeln erhält man auch ganz brauchbare Ergebnisse. Die Soundkarte und das Programm können die Daten selbst dann schnell genug auswerten, wenn man über keinen sehr schnellen Rechner verfügt.

Das größte Problem liegt darin, die Kugel direkt über der ersten Lichtschranke sicher zu haltern.

Holzkugeln sind zu leicht, bei ihnen macht sich der Luftwiderstand doch schon deutlich bemerkbar.