Längenkontraktion.
1.) Strecken in Bewegungsrichtung.
Welche Strecke legt ein schneller "Zug" innerhalb einer
Lichtsekunde zurück?
Der blaue Punkt bezeichnet die Stelle, an der sich die Lichtuhr beim Start
befunden hat.
Zur Messung der zurückgelegten Strecke, benutzen wir die Lichtuhr im Zug,
so wie wir sie von den jeweiligen Bezugssystemen aus sehen.
| vom ruhenden System aus betrachtet | vom bewegten System aus betrachtet |
| Vom ruhenden System aus betrachtet, ist der Bahnsteig in Ruhe. |
Vom bewegten System aus betrachtet, ist der Zug in Ruhe und in ihm auch die
Lichtuhr. |
| Der Zug bewegt sich mit der Geschwindigkeit v nach rechts, ebenso die
Lichtuhr im Zug. |
Der Bahnsteig bewegt sich mit der Geschwindigkeit v nach links. |
| Die Zeit, bis der Lichtpunkt wieder am unteren Rand ankommt, ist Δtr. | Die Zeit, bis der Lichtpunkt wieder am unteren Rand ankommt, ist Δtb. |
| Die zurückgelegte Strecke ist s = v * Δtr | Die zurückgelegte Strecke ist s' = v * Δtb |
Die Geschwindigkeit v, mit der sich die beiden Bezugssysteme
relativ zueinander bewegen, ist für beide Systeme vom Betrag her
gleich.
Da die Zeit Δtr größer
als Δtb ist (vgl. Seite Zeitdilatation), ist auch die Strecke
s größer als die Strecke
s'
Dabei gilt für den Zusammenhang zwischen Δtr und Δtb

Für die Längen gilt also:
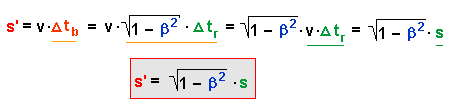
Da β = v / c wird der Wurzelfaktor um so kleiner, je
größer die Geschwindigkeit v wird.
Vom bewegten System aus erscheinen also Längen in der
Bewegungsrichtung verkürzt oder kontrahiert. Man spricht von
Längenkontraktion.
Ein Beispiel:
Der "Superzug" bewege sich mit 3/4 Lichtgeschwindigkeit. Dann ist
β = v / c also 0,75 also β2 = 0,5625.
Damit steht unter der Wurzel 0,4375 und der Wurzelausdruck wird 0,661.
Wenn wir (System Bahnsteig) also sagen, der "Zug" sei s = 100 m weit nach rechts gefahren, dann sagt der Beobachter im Zug, der Bahnsteig hat sich um s' = 66.1 m nach links bewegt.
2.) Strecken quer zur Bewegungsrichtung.
Beachte, dass Strecken quer zur Bewegungsrichtung nicht verkürzt werden.
Wäre dies so, dann würde für einen Beobachter in einem
"Superzug", der auf einen Tunnel zurast, das Tunnelportal zu einem
engen Nadelöhr schrumpfen, durch das der Zug niemals passen würde!
Ein ruhender Beobachter am Tunneleingang würde dagegen einen auf
"Spielzeuggröße" geschrumpften Zug sehen, und hätte
keinen Zweifel, dass der "locker durch die Tunnelröhre
passt".
Es darf natürlich nicht vom Beobachter abhängen, ob der Zug durch den
Tunnel kommt oder nicht!
3.) Weiterführende Seiten.
 |
Relativistischer Flug durch ein Gitter: http://www.tempolimit-lichtgeschwindigkeit.de/relaflug/relaflug.html |
 |
Fast lichtschnell durch die Stadt http://www.tempolimit-lichtgeschwindigkeit.de/tuebingen/tue0.html |
Das Java-Applet auf dieser Seite basiert auf Physlets von
Wolfgang Christian. (Davidson College) |


