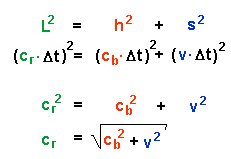Lichtuhren und Zeitdilatation.

Für die Simulation mit dem Java-Applet muss im Browser Java und Java-Script Wiedergabe aktiviert sein.

1.) Die Idee der Lichtuhr.

Die Zeiten in einem bewegten Bezugssystem und einem ruhenden Bezugssystem sollen mit Hilfe einer sogenannten "Lichtuhr" genauer betrachtet werden.

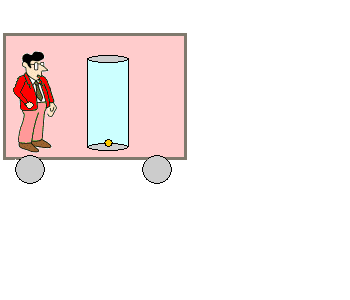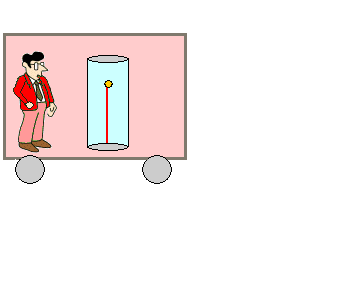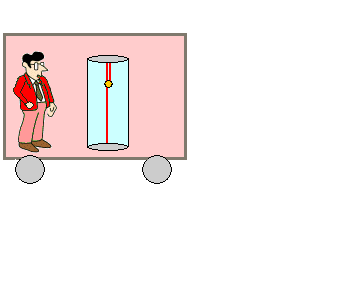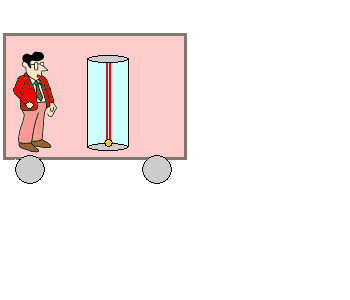
Vom Boden einer Art Standzylinder geht ein Lichtsignal aus. Dieses läuft gleichförmig zum oberen Ende des Zylinders, wo sich ein Spiegel befindet. Das Lichtsignal wird dadurch zurückgeworfen und trifft, wie bei einem Echo, wieder auf den Boden auf, wo es einen Zähler weiterzählt.

Der Standzylinder der Lichtuhr sei z.B. 15 cm hoch.
Dann ist die Wegstrecke, die das Licht zurücklegt, bis der Zähler erhöht wird 30 cm = 0,3 m.
Breitet sich das Licht mit c = 300.000 km/s = 3*10⁸ m/s aus, so wird der Zähler jeweils nach 1 ns = 1*10^-9 erhöht (t = s / c)

2.) Es kommt auf den Standpunkt an.

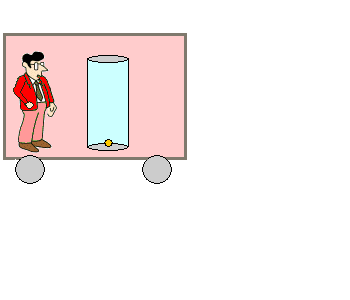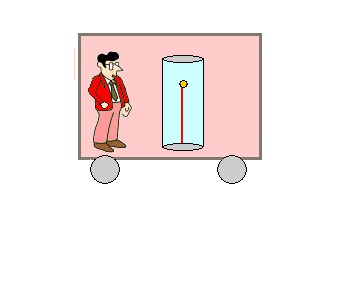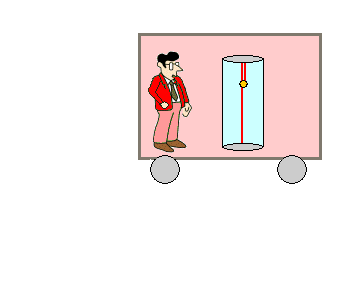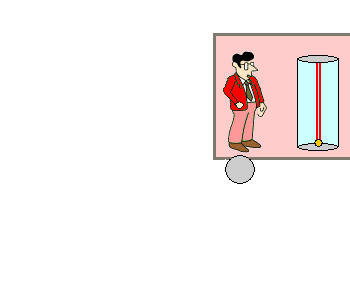
Vom bewegten Beobachter aus gesehen.

Nun befinde sich die Lichtuhr in einem Zugwagen, der mit großer, gleichbleibender Geschwindigkeit von links nach rechts fährt.

Für den bewegten Beobachter Bernd, der im selben Bezugssystem wie die Lichtuhr ist, ist die Sache einfach: für ihn läuft der Lichtstrahl immer senkrecht auf und ab.
Ob der Zug steht oder mit konstanter Geschwindigkeit fährt, macht für ihn in seinem Inertialsystem keinen Unterschied. Der Lichtstrahl bleibt immer "vor seiner Nase" und macht eine Bewegung zuerst aufwärts und dann abwärts. (Versuche mit den Augen von Bernd zu sehen)

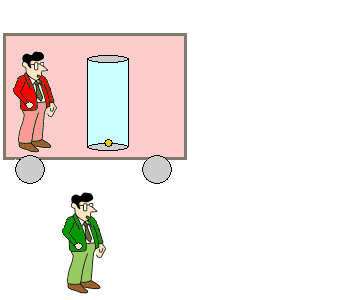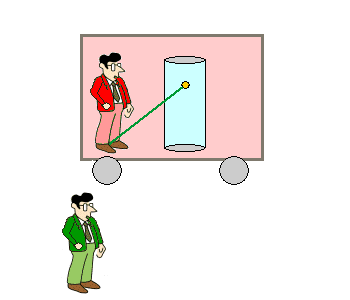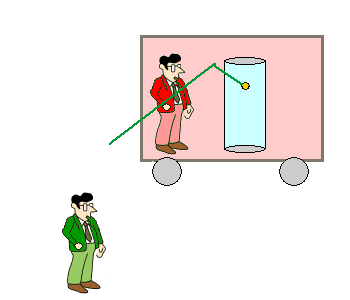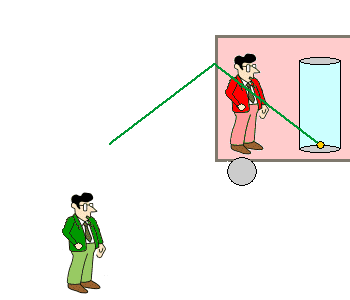
Vom ruhenden Beobachter aus gesehen Der auf dem Bahnsteig stehende, ruhende Beobachter Rudi sieht etwas anderes, wenn der Zug mit der Lichtuhr mit konstanter Geschwindigkeit an ihm vorbeifährt und er die Position des gelben Lichtpunkts mit den Augen verfolgt. Für ihn durchläuft der Lichtstrahl die grün eingezeichnete Bahn. Weil sich hier zwei gleichförmige Bewegungen überlagern, ist die Bahn dreieckförmig. ( Die gelbe Kugel ist kein "Ball", der würde bei einem senkrechten Wurf nach oben gebremst und anschließend beim freien Fall nach unten wieder beschleunigt. Es ist ein Lichtpunkt, der sich mit konstanter Lichtgeschwindigkeit bewegt. )

3.) Ein klassisches Modell wird zunächst benutzt.

( gleiche Zeitintervalle - unterschiedliche Geschwindigkeiten.)

Die Überlagerung zweier gleichförmiger Bewegungen kennt man vielleicht von einer (nicht an einem Seil geführten) Fähre, die einen Fluss überquerrt.
Diese Bewegung wollen wir zunächst einmal als Modell für die Bewegung des Lichtstrahls bei der Lichtuhr betrachten.

3.1.) Beschreibung der Bewegung.

b) Bewegter Beobachter.

Auf der Fähre bleibt ein Autofahrer während der Überfahrt im seinem Auto sitzen.
Im Inneren des Fährschiffes sieht er nichts von der Landschaft um ihn herum, und er bemerkt auch nichts von der konstanten Strömung des Flusses.
Er muss daher annehmen, dass die Fähre das andere Ufer in B - genau auf der gegenüberliegenden Seite - erreicht, dass sie den Fluss also auf der Strecke h überquert.

a) Ruhender Beobachter.

Genau über der Fähre beobachtet ein ruhender Beobachter in einem Heißluftballon den Vorgang von oben:

Die Fähre fährt mit konstanter Geschwindigkeit von A aus über den Fluss und peilt das gegenüberliegende Ufer in B an. (dies entspricht der Ausbreitung des Lichtstahls)
Gäbe es keine Strömung , würde die Fähre auch dort ankommen. Durch die konstante Strömung mit der Geschwindigkeit v wird die Fähre aber um Ds abgetrieben und erreicht das gegenüberliegende Ufer etwas flussabwärts in C.
(dies entspricht der Bewegung des "Zuges")
Wie weit die Fähre abgetrieben wird, hängt davon ab, wie groß die Geschwindigkeit der Fähre c_b und die Strömungsgeschwindigkeit v des Flusses ist.
Für den ruhenden Beobachter legt die Fähre die Strecke L zurück.

3.2.) Wie beurteilen die beiden Beobachter die Geschwindigkeit der Fähre?

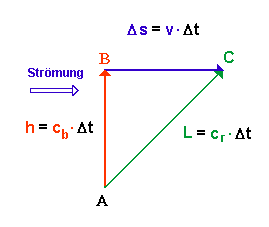
Annahme: die Dauer der Überfahrt Dt ist für beide Beobachter die gleiche.

Bewegter Beobachter im Inneren der Fähre.

Die Fähre legt die Strecke h zurück.

Sie hat die Geschwindigkeit c_b.

Es gilt h = c_b * Dt.

Ruhender Beobachter (Ballon)

Die Fähre wird abgetrieben, sie muss daher die längere Strecke L zurücklegen

Es gilt der Satz des Pythagoras:

Pythagoras

Für den ruhenden Beobachter (Ballon) bewegt sich die Fähre also schneller, weil zur Geschwindigkeitskomponente des Boots (c_b) auch noch die Geschwindigkeitskomponente der Strömung (v) hinzukommt. So kann die größere Strecke L in derselben Zeit Dt zurückgelegt werden.

4.) Ja, aber ....... - Die Grenzen des Modells.

Für das Fährenproblem ist die Beschreibung gut geeignet.

Wir haben es aber nur als Modell für die Verhältnisse bei der Lichtuhr benutzt!

Jetzt ist aber bei der Lichtuhr die Geschwindigkeit c_b die Lichtgeschwindigkeit c.
Damit müsste sich für den ruhenden Beobachter das Licht mit einer größeren Geschwindigkeit als der Lichtgeschwindigkeit c ausbreiten, was nicht möglich ist.

Nach den Maxwell-Gleichung der elektromagnetischen Wellen ist die Lichtgeschwindigkeit im Vakuum

Da die Dielektrizitätszahl e₀ und die Permeabilitätszahl m₀ Naturkonstanten sind, ist es die Lichtgeschwindigkeit auch.
Sie kann nicht einfach durch Wechsel des Bezugssystems größer oder kleiner werden!

Wenn die Lichtgeschwindigkeit in allen Bezugsystemen gleich ist, dann muss c_b = c_r = c sein.
Dann kann aber das Zeitintervall Dt in beiden Systemen nicht mehr dasselbe sein!
Die Zeitintervalle in beiden Systemen müssen dann unterschiedlich lang sein!

Wärend wir also klassisch davon ausgehen, dass Dt in allen Systemen gleich ist und daher die Geschwindigkeiten verschieden sind, erzwingt die Tatsache, dass die Lichtgeschwindigkeit in allen System gleich sein muss, dass es die Zeitintervalle nun nicht mehr sein können.

5.) Relativistischer Zusammenhang zwischen Zeit und Geschwindigkeit.

(gleiche Geschwindigkeiten - unterschiedliche Zeitintervalle)

Betrachten wir also wieder das Dreieck mit dem Satz von Pythagoras, lassen aber diesmal die Lichtgeschwindigkeit in beiden Sytemen gleich und setzen unterschiedliche Zeitintervalle Dt_r und Dt_b an.

Dann ergibt sich aus der Sicht des ruhenden Beobachters ("Bahnsteig"):

Relativistische Betrachtung der Bewegung

Interpretation der Gleichung:

kleine Geschwindigkeiten
bewegt sich der Zug mit einer Geschwindigkeit v << c ( so wir es aus dem Alltag gewohnt sind), dann ist der Faktor b sehr klein. Der Wurzelfaktor unterscheidet sich dann kaum von "1".

Vergeht im bewegten System ("Zug") eine Lichtsekunde, dann vergeht für den ruhenden Beobachter ("Bahnsteig"), der die Lichtuhr im Zug sieht, praktisch auch eine Lichtsekunde.
Die Zeitspannen in beiden Systemen unterscheiden sich nicht merklich.
große Geschwindigkeiten
bewegt sich der Zug mit großer Geschwindigkeit, geht also v gegen c, dann geht der Ausdruck b gegen "1", d.h. der Wurzelausdruck strebt gegen 0.

Also ist nun Dt_r >Dt_b.
Dem Beobachter im ruhenden System ("Bahnsteig") erscheint es so, als ob die Zeit im bewegten System ("Zug") verlängert oder gedehnt wäre.
Man nennt dies Zeitdehnung oder Zeitdilatation.
Vom ruhenden System aus gesehen, scheint die Zeit im bewegten System langsamer zu vergehen.

6.) Eine Animation macht die Sachverhalte deutlicher.

In dieser Animation siehst du zwei Lichtuhren. Die rote Uhr ist die Uhr, die sich im System des bewegten Beobachters ("im Zug") befindet. Die grüne Uhr ist die Lichtuhr, vom ruhenden System ("Bahnsteig") aus gesehen.

Lasse den Zug fahren, indem du einen Faktor b größer 0 eingibst.
Je größer dieser Faktor wird, desto schneller bewegt sich das Bezugssytem. Bei Faktor 0.9 fährt dein "Zug" mit 90% Lichtgeschwindigkeit!
Beachte auch, dass die Breite der Lichtuhr kontrahiert erscheint.

Bitte warten Sie, bis die Animation vollständig geladen ist.

Die folgenden Bildausschnitte sollen das noch besser verdeutlichen. Es zeigt drei ausgewählte Zeitpunkte für b = 0,7.

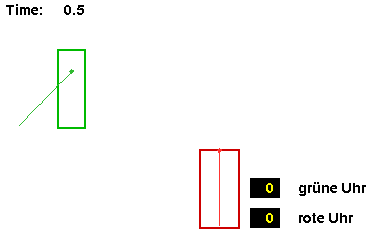Für den bewegten Beobachter hat der Lichtstrahl gerade den Spiegel erreicht, für ihn ist 0,5 Lichtsekunden vergangen.

Für denjenigen, der die Lichtuhr vom ruhenden System aus sieht, hat der Lichtstrahl den Spiegel noch nicht erreicht, Für ihn ist weniger als 0,5 Lichtsekunden vergangen.

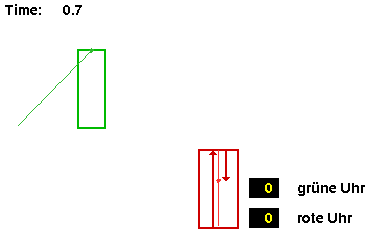Aus dem ruhenden System aus gesehen hat der Strahl der Lichtuhr den Spiegel gerade erreicht. Für den ruhenden Beobachter ist im Zug also gerade 0,5 Lichtsekunden vergangen.

Für den bewegten Beobachter ist der Strahl der Lichtuhr bereits auf dem Rückweg. Für ihn sind mehr als 0,5 Lichtsekunden vergangen.

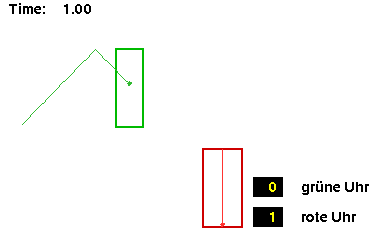Für den bewegten Beobachter erreicht der Lichtstrahl gerade den Boden der Lichtuhr. Für ihn ist 1 Lichtsekunde vergangen. Seine Eigenzeit ist 1 Lichtsekunde.

Der ruhende Beobacher sieht den Strahl noch auf dem Rückweg. Für ihn ist im bewegten System weniger als 1 Lichtsekunde vergangen.

Das Java-Applet ist in der Reihe Physlets entstanden:
Exploration authored by Anne J. Cox.
Script authored by Anne J. Cox and Wolfgang Christian.
Applet authored by CoLoS and modified by Wolfgang Christian.

Animationen: Klaus-Dieter Grüninger, Landesbildungsserver

Fachgruppe Physik