Der Dopplereffekt - bewegte Schallquelle, ruhender Beobachter.

0.) Was ist der Dopplereffekt?

Heute kennen wir den Dopplereffekt aus dem Alltag, wir nehmen ihn immer dann wahr, wenn ein Fahrzeug schnell an uns vorbeifährt.

Was hörst du dabei?

Die Töne der Motoren haben für dich nicht immer dieselbe Tonhöhe (Frequenz), sondern sie verändern sich, während das Fahrzeug an dir vorbeifährt.
Kommt das Fahrzeug auf dich zu, so erscheint der Ton höher, bewegt er sich von dir weg, so erscheint er tiefer, auch wenn der Fahrzeugmotor immer denselben Ton aussendet.


(Video: LKW auf der B29 bei Schwäbisch Gmünd, Diesellok auf der Bodenseebahn bei Langenargen, Flugzeugstart auf dem Landesflughafen in Stuttgart)

Noch extremer ist der Effekt wenn ein Formel-I Rennwagens an der Zuschauertribüne vorbeifährt.
Obwohl die Geschwindigkeit des Rennwagens - und damit die Motorfrequenz - konstant sind, hört man auf der Tribüne eine deutliche Frequenzänderung von hoch nach tief.


(Video von Christian Borgmann auf YouTube)

Ein bewegter Schallerzeuger sendet eine konstante Frequenz f aus.
Du hörst eine größere Frequenz (höherer Ton) fv, wenn sich der Schallerzeuger auf dich zu bewegt.
Bewegt er sich von dir weg, so hörst du eine kleinere Frequenz (tieferer Ton) fh.
Die Frequenzverschiebung Δf gegenüber der Originalfrequenz f ist um so größer, je größer die Geschwindigkeit v des Schallerzeugers ist.
  • Wodurch kommt dieser Effekt zustande?
  • Was wird hier verdoppelt?

Um die zweite Frage zuerst zu beantworten: hier wird gar nichts verdoppelt!

Der Name Dopplereffekt hat auch nichts mit Verdoppeln zu tun, sondern ist nach dem österreichischen Physiker Christian Doppler (1803 - 1853) benannt, der diesen Effekt erstmals postuliert hat.
Mehr zu Christian Doppler findet man beispielsweise hier https://de.wikipedia.org/wiki/Christian_Doppler
Viele seiner damaligen Kollegen nahmen ihn nicht ernst und verlachten seine Theorie. Es war die Zeit der Postkutschen, die Zeit, in der die ersten Eisenbahnen kaum mehr als 50 km/h erreichten. Die Frequenzverschiebungen bei Schallwellen konnten nur von Menschen mit absolutem Gehör ansatzweise wahrgenommen werden.

Eine erste Idee, was dieser Dopplereffekt ist, bekommst du hier bei 100sPhysik auf YouTube:

Wir wollen hier aber noch einen Schritt weiter gehen, und Dopplers Theorie Schritt für Schritt herleiten und jeweils dazu eine Beispielrechnung machen.

1.) Grundlagen der gleichförmigen Bewegung und die Wellenlänge λ.

Wir sollten uns an folgende Grundlagen einer Welle erinnern:

Allgemeine gleichförmige Bewegung
(Bewegung mit konstanter Geschwindigkeit v)		 Gleichförmige Schallausbreitung
(Bewegung mit konstanter Schallgeschwindigkeit c)
Für die gleichförmige Bewegung gilt:
s = v * t.

Die zurückgelegte Wegstrecke s ist das Produkt aus Geschwindigkeit v und Zeit t.

Sie nimmt also linear mit der Zeit zu.		 Auch Schall breitet sich mit der konstanten Geschwindigkeit c aus. Sie ist in Luft etwa 340 m/s.
In der Zeit t legt der Schall also die Strecke s = c * t zurück.

Dies ist genau der gleiche Zusammenhang wie bei der allgemeinen gleichförmigen Bewegung, nur ist die allgemeine Geschwindigkeit v durch die Schallgeschwindigkeit c ersetzt.

Eine wichtige Größe für die Beschreibung von Schwingungen ist die Periodendauer T. Es ist die Zeit, in der eine komplette Schwingung erfolgt, bevor der Schwingungsvorgang neu beginnt. Die Periodendauer T ist der Kehrwert der Frequenz f.

Während einer Periode T kommt also die ausgesandte Schallwelle um die Strecke λ = c * T voran.
Diese Strecke nennt man die Wellenlänge λ.


Mehr dazu findest du auch im Bereich mechanische Schwingungen.

2.) Skizzen zur Schallausbreitung.

Wir wollen uns Momentaufnahmen der Wellen immer genau im zeitlichen Abstand T ansehen, um die Dinge etwas zu vereinfachen.

Skizze Kommentierung
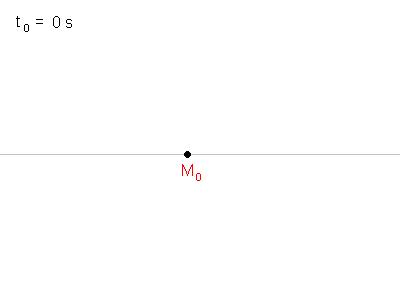Beim Start der Betrachtung Die Quelle beginnt zum Zeitpunkt t0  = 0 s im Punkt M0 mit dem Aussenden einer ersten Welle.

Der Erreger bewegt sich mit der Geschwindigkeit v nach rechts.
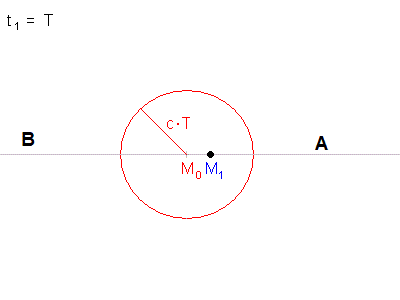Situation nach einer Periode Nach einer Periode T ist die erste Welle um eine Wellenlänge λ = c * T vorangekommen. (roter Kreis - räumlich eine Kugelschale)

Der Erreger selbst ist in dieser Zeit um die Strecke s =  v * T nach rechts vorangekommen. Er ist nun bei M1.

Hier beginnt er mit dem Aussenden der zweiten Welle (blau).
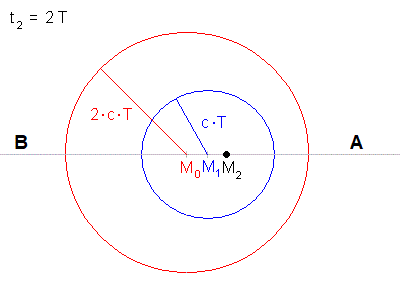Situation nach zwei Perioden Nach zwei Perioden (2 * T) ist die zum Zeitpunkt t0 ausgesandte Welle um 2 * λ = 2 * c * T vorangekommen (roter Kreis), die zum Zeitpunkt t1 ausgesandte Welle um λ = c * T (blauer Kreis).

Die Zentren der beiden Kreise sind aber verschoben, weil der Erreger ja die zweite Welle (blau) von weiter rechts abgestrahlt hat.

Der Erreger befndet sich jetzt um die Strecke s = 2 * v * T vom Startpunkt entfernt bei M2.

Er beginnt mit dem Aussenden der dritten Welle.

Könntest du ein Momentbild für den Zeitpunkt t3 = 3 * T zeichnen?

Dann ist die in M0 erzeugte Welle um die Strecke 3 * λ = 3 * c * T vorangekommen (roter Kreis).
Die in M1 erzeugte Welle um die Stecke 2 * λ = 2 * c * T (blauer Kreis) und die in M2 erzeugte Welle um die Strecke λ = c * T (neuer Kreis).

Der Erreger selber ist dann an einem Punkt M3 noch einmal um die die Strecke v * T weiter nach rechts gekommen, insgesamt also nun um die Strecke s = 3 * v * T vom Startpunkt M0 entfernt.

3.) Was hört der Beobachter A, auf den die Quelle zukommt?

In dieser Skizze sind nur die Strecken für einen Beobachter A rechts von der Quelle ("vorn") eingetragen. Die Quelle kommt auf ihn zu.

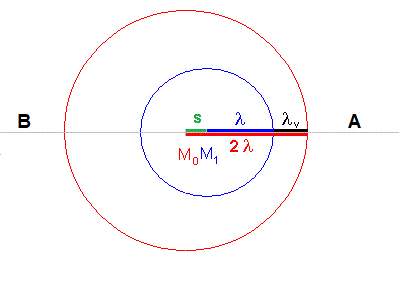 Strecken für Beobachter A Aus der Skizze liest man ab, dass dabei gilt:
{short description of image}

Dabei ist λ die Wellenlänge der ruhenden Quelle.
Die Wellenlänge λv, die der Bebachter A wahrnimmt, ist also die Wellenlänge der ruhenden Quelle λ minus der Strecke s, um die die Quelle in der Zeit T voran kommt.

Mit der Periodendauer T lässt sich diese Beziehung auch folgendermaßen schreiben:
{short description of image}

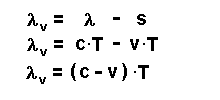
oder mit T = 1 / f umgeformt:
{short description of image}

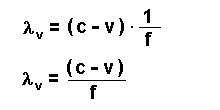
Welche Frequenz fv hört aber der Beobachter in A nun?

Es gilt: c = f * λ - also gilt auch c = f v * λ v bzw. λ v = c / f v.

Damit ergibt sich:
{short description of image}

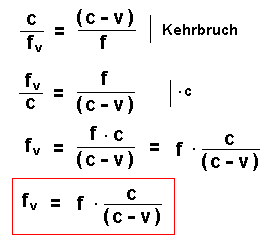
Ein Beispiel:
Die Hupe eines fahrenden Autos ertönt mit f = 800 Hz. Das Auto fährt mit 72 km/h (=20 m/s) auf den Beobachter A zu.
Welche Frequenz hört er?
Beispielrechnung
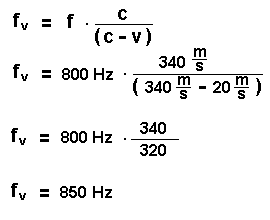
Der Ton der Hupe scheint ihm also um 50 Hz höher im Vergleich zum stehenden Fahrzeug.

In manchen Herleitungen findet man auch folgende äquivalente Formulierung:
äquivalente Formulierung

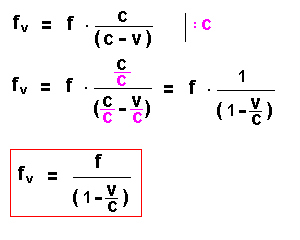
Zusammenfassung:
Der Beobachter A, auf den die Quelle zufährt, hört die Frequenz fv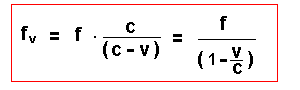
Frequenz für den Beobachter, auf den das Fahrzeug zufährt
Sie ist gegenüber der Originalfrequenz f erhöht.

4.) Was hört der Beobachter B, von dem sich die Quelle wegbewegt?

Wenn wir das bis hierher verstanden haben, fällt es nicht schwer die äquivalenten Betrachtungen für den Beobachter B aufzustellen. Er ist "hinter" der Quelle, diese bewegt sich also von ihm weg.
Wir sehen uns zunächst wieder die Skizze an und stellen eine Beziehung für die Strecken auf:

Strecken für Beobachter B Streckenbeziehungen
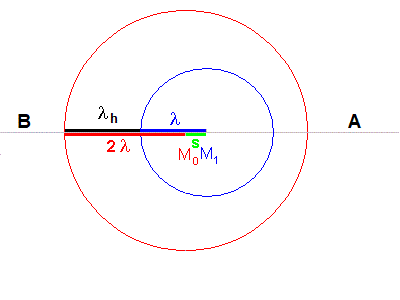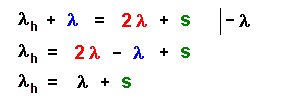Dabei ist λ wieder die Wellenlänge der ruhenden Quelle.
Die Wellenlänge λh, die der Bebachter B wahrnimmt, ist also die Wellenlänge der ruhenden Quelle λ plus der Strecke s, um die die Quelle in der Zeit T voran kommt.

Dies ist genau wie für den Beobachter A, nur dass dort von der Wellenlänge λ die Strecke s abgezogen wird. Beim Beobachter B wird hingegen die Strecke s zur Wellenlänge λ addiert.

Eigentlich ist dies auch schon anschaulich klar, denn die Mittelpunkte des roten und des blauen Kreises sind um die Strecke s (Abstand M0 - M1) verschoben.
Damit muss sich der Abstand der beiden Kreise auf der Bewegungslinie (grau) ebenfalls um s verändern.
Rechts (vorn, bei A) ist er um die Strecke s verkleinert, links (hinten, bei B) um die gleiche Strecke s vergrößert.

Zur besseren Übersicht fassen wir einmal kurz zusammen:

Beobachter A - Quelle bewegt sich auf ihn zu Beobachter B - Quelle bewegt sich von ihm weg
Er beobachtet die Wellenlänge λv,
sie ist gegenüber der Wellenlänge λ verkleinert.		 Er beobachtet die Wellenlänge λh,
sie ist gegenüber der Wellenlänge λ vergrößert.
{short description of image} {short description of image}

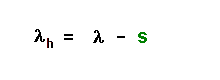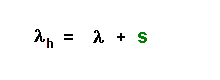Welche Frequenz fh hört der Beobachter in B?

Wir können also die gleichen Herleitungsschritte wie oben durchführen und müssen dabei lediglich jeweils das Minuszeichen durch ein Pluszeichen ersetzen.

{short description of image}

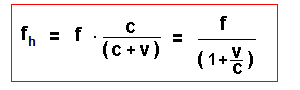
Und hier wieder unser Zahlenbeispiel für den Beobachter B:
Die Hupe eines fahrenden Autos ertönt mit f = 800 Hz. Das Auto fährt mit 72 km/h (=20 m/s) vom Beobachter B weg.
Welche Freqeunz hört er?
{short description of image}

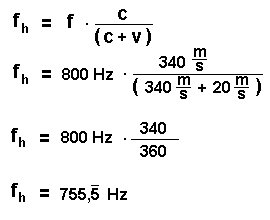
5.) Was passiert, wenn die Geschwindigkeit des Erregers sich der Schallgeschwindigkeit nähert, bzw. so groß wie die Schallgeschwindigkeit wird?

{short description of image}
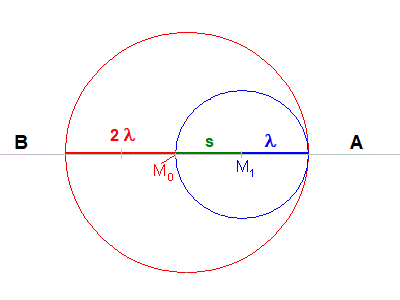
Bewegt sich die Quelle auf den Beobachter A mit der Schallgeschwindigkeit c zu, so ist die Wellenlänge λv gleich 0 (die beiden Wellenkreise berühren sich).
Das heißt die Frequenz f v wird für v --> c sehr groß (geht gegen unendlich), der Beobachter hört einen extrem hohen Ton, bzw. gar keinen mehr, wenn die Frequenz oberhalb der Hörgrenze ( > etwa 15.000 bis 20.000 Hz) liegt.

Für den Beobachter B nimmt die Wellenlänge λh in diesem Fall den Wert 2*λ an, er hört also die Hälfte der Originalfrequenz.

Daran erkennt man, dass die Frequenzverschiebung für Beobachter A und B nicht die gleiche ist. Dies erkennt man in dern Beispielrechnungen auch schon ein klein wenig.
Ist aber v << c, dann sind die Frequenzverschiebungen für beide Beobachter beinahe identisch.

6.) Was geschieht, wenn sich die Quelle schneller als der Schall bewegt, wenn also v > c ist?

In diesem Fall ist s größer als λ, die Quelle "überholt" die von ihr ausgesandten Wellen. Vor dem Errreger befinden sich nun eng beieinander liegende Wellen.
Mach Kegel
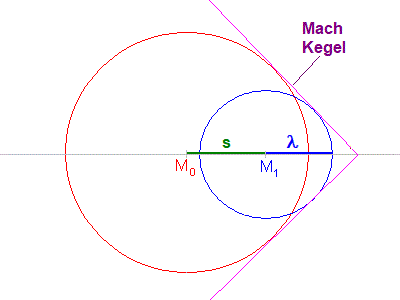
Daher ist der Druck an dieser Stelle sehr hoch. Dies gilt auch für jedem anderen Punkt der violetten Verbindungslinien (vgl. Skizze).
Räumlich liegen all diese Punkte auf einem Kegelmantel. Man spricht vom Machschen Kegel, benannt nach Ernst Mach - österreichischer Physiker (1838 - 1916).
Wikipedia zu Ernst Mach

Jeder Beobachter, der sich an einem Punkt auf diesem Kegelmantel befindet, hört einen lauten Knall, den Überschallknall.
Solche Machschen Kegel entstehen also, wenn die Geschwindigkeit v der Quelle größer als die Schallgeschwindigkeit c ist.
Im Grenzfall entsteht der Knall auch schon bei v = c also bei einer Geschwindigkeit von 340 m/s bzw. 1224 km/h. Man nennt diese Geschwindigkeit dann auch 1 Mach oder Mach 1.

In der Praxis kommen solchen Geschwindigkeiten durchaus vor.
Militärische Düsenjets erreichen diese Geschwindigkeiten mühelos, dürfen sie - aus den oben genannten Gründen - über bewohnten Gebieten aber nicht fliegen.
Normale Verkehrsflugzeuge bleiben bei Geschwindigkeiten von 900 - 1000 km/h unter Mach 1.

Auch spezielle Verkehrsflugzeuge (Concorde, Tupolew Tu-144) erreichen solche Geschwindigkeiten. Auffällig ist die Ähnlichkeit der beiden Flugzeuge (Teil "Industriespionage").
Die französisch-englische Concorde durfte mehr als 1 Mach auch nur über dem unbewohnten Atlantik fliegen. Nach einem Unfall beim Start wurden die Flüge mit der Concorde 2003 eingestellt, da ihre Wirtschaftlichkeit zudem in Frage stand.
Aus dem gleichen Grund wurden Flüge mit der russischen TU-144 schon viel früher eingestellt.

Beide Flugzeuge gibt es heute nebeneinander im baden-württembergischen Technikmuseum in Sinsheim zu bestaunen, sie können auch von innen besichtigt werden.
Sie sind zumindest ein faszinierendes Stück Technikgeschichte.

7.) Weiterführende Links

Den Dopplereffekt für ruhende Quelle und bewegten Beobachter findest du hier: Dopplereffekt - ruhende Schallquelle, bewegter Beobachter

Vergleich der beiden Dopplereffekte: Dopplereffekt - Vergleich der beiden Möglichkeiten

Grüninger, Landesbildungsserver, 2018